Recursividad parte2
Summary
TLDREl guion del video explica cómo funciona la recursividad en la programación, utilizando el ejemplo del cálculo del factorial de un número. Se describe el proceso de llamar una función a sí misma con un parámetro reducido hasta que se cumple una condición base. Se simula paso a paso cómo se ejecuta el programa, mostrando cómo se guardan y recuperan los estados en la pila de llamadas para regresar a los puntos de ejecución anteriores, ilustrando así la naturaleza de las funciones recursivas y su implementación en lenguajes de programación como C.
Takeaways
- 📝 La función factorial se puede implementar de manera recursiva en C.
- 🔄 La recursividad implica que una función se llama a sí misma hasta alcanzar una condición base.
- 🔢 El factorial de un número se calcula multiplicando ese número por todos los números menores hasta llegar al uno.
- 🌐 Se simula el proceso paso a paso para comprender cómo funciona la recursividad.
- 💡 Se utiliza el ejemplo del factorial de 4 para explicar cómo funciona la recursividad en detalle.
- 📚 Se menciona que la condición base para detener la recursión es cuando n es igual a 0.
- 🔄 Se describe el proceso de llamada y retorno de funciones recursivas como una pila, donde se guardan los estados.
- 💾 Se explica que la pila de memoria es fundamental para que el programa recuerde dónde continuar después de una llamada recursiva.
- 🔙 Se destaca la importancia de devolver valores de las funciones para que se puedan calcular los factoriales de los parámetros anteriores.
- 🛠️ Se ilustra cómo se guardan y recuperan valores de la pila para mantener el estado de la ejecución entre llamadas recursivas.
Q & A
¿Qué es un factorial y cómo se calcula?
-El factorial de un número entero positivo n, representado como n!, es el producto de todos los números enteros positivos desde 1 hasta n. Se calcula multiplicando n por todos los números menores que él hasta llegar al 1.
¿Qué es una función recursiva y cómo se relaciona con el ejemplo del factorial?
-Una función recursiva es aquella que se llama a sí misma dentro de su definición. En el ejemplo del factorial, la función se llama a sí misma con un parámetro reducido hasta que alcanza la condición de base (n = 0), lo que permite calcular el factorial de manera iterativa sin utilizar bucles.
¿Cómo se representa la condición de base en la función recursiva del factorial?
-La condición de base en la función recursiva del factorial se representa con la condición 'n == 0', que cuando se cumple, la función devuelve 1, lo que es el factorial de 0.
¿Qué sucede si la condición de base no se cumple en una función recursiva?
-Si la condición de base no se cumple, la función recursiva continuará llamando a sí misma con un nuevo parámetro hasta que finalmente se cumpla la condición y pueda devolver un valor.
¿Cuál es el parámetro inicial que se utiliza para calcular el factorial de 4 en el ejemplo?
-El parámetro inicial utilizado para calcular el factorial de 4 en el ejemplo es el número 4 mismo, ya que se desea calcular 4!.
¿Qué papel juega la pila en la ejecución de funciones recursivas?
-La pila es un espacio en memoria que guarda temporalmente los valores necesarios para que una función recursiva pueda regresar a su estado anterior después de cada llamada. Almacena direcciones y valores de parámetros que permiten la navegación correcta a través de las llamadas recursivas.
¿Cómo se resuelve la llamada recursiva cuando se llega al factorial de 1 en el ejemplo?
-Cuando se llega al factorial de 1 en el ejemplo, ya no se hace ninguna llamada recursiva adicional, ya que el factorial de 1 es conocido (1! = 1), y se devuelve ese valor a la llamada anterior.
¿Qué significa el término 'retornar' en el contexto de funciones recursivas?
-En el contexto de funciones recursivas, 'retornar' significa devolver un valor a la llamada de la función que invocó la recursión, permitiendo así la resolución de la operación y el avance en el cálculo del factorial.
¿Cómo se demuestra la eficacia de la recursividad en el cálculo del factorial sin utilizar bucles?
-La eficacia de la recursividad en el cálculo del factorial se demuestra al mostrar que, a pesar de no utilizar bucles como while o for, se puede realizar el cálculo de manera efectiva y eficiente a través de la repetida invocación de la función a sí misma con parámetros adecuados.
¿Cuál es la ventaja de usar recursividad en problemas como el cálculo del factorial?
-La ventaja de usar recursividad en problemas como el cálculo del factorial es que permite una solución clara y elegante al problema, simplificando el código y haciendo que sea más fácil de entender y mantener, a pesar de que en algunos casos pueda tener un overhead de memoria debido al uso de la pila.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频

Qué son las FUNCIONES RECURSIVAS ➤ CURSO en C#

La MAGIA de la RECURSIVIDAD

CLASE 1 - ENCENDIDO Y APAGADO DE UN LED CON UN PULSADOR / BOTON - TINKERCAD | ARDUINO
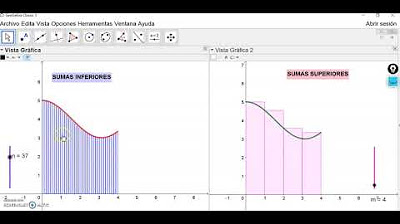
SUMAS DE RIEMANN

📌🖥️Calculo ISR de nominas, salarios y personas físicas 📍(Tutorial) y ejemplo👩🏻💻🧮

Introducción al cálculo integral | Khan Academy en Español
5.0 / 5 (0 votes)
