INTERSECCIONES DE UNA GRÁFICA CON LOS EJES X e Y 📈
Summary
TLDREn este vídeo se explica cómo encontrar las intersecciones de la gráfica de la función y = x^3 - 4x con los ejes X e Y. Al igualar y a 0, se resuelve la ecuación para encontrar los puntos en el eje X, obteniendo x = -2, x = 2 y x = 0. Al igualar x a 0, se determina que la intersección con el eje Y es en el punto (0, 0). Se describen los pasos de factorización y se visualiza el bosquejo de la gráfica con los puntos de intersección.
Takeaways
- 📉 En el video se busca determinar las intersecciones de la gráfica de la función y = x^3 - 4x con los ejes X e Y.
- 🔄 Para encontrar las intersecciones con el eje X, se iguala y a 0, lo que da la ecuación x^3 - 4x = 0.
- 🧮 El siguiente paso es factorizar x^3 - 4x, encontrando que se puede factorizar como x(x^2 - 4) = 0.
- ✂️ Luego, se aplica la diferencia de cuadrados a x^2 - 4, lo que resulta en x(x - 2)(x + 2) = 0.
- 🔢 Los factores se igualan a 0, generando tres soluciones para x: x = -2, x = 2 y x = 0.
- 📍 Esto indica que las intersecciones con el eje X son en los puntos (-2, 0), (2, 0) y (0, 0).
- ✖️ Para encontrar la intersección con el eje Y, se iguala x a 0 en la ecuación original.
- ⚖️ Al hacer x = 0, se concluye que y = 0, lo que genera una única intersección en el origen (0, 0).
- 🗺️ Se hace un bosquejo de la gráfica, mostrando los puntos de intersección con los ejes X e Y.
- 📊 El video muestra un método sistemático para hallar intersecciones mediante factorización y análisis de la función.
Q & A
¿Qué objetivo tiene el vídeo?
-El objetivo del vídeo es determinar las intersecciones que tiene una gráfica con los ejes X e Y, específicamente para la función y = x^3 - 4x.
¿Cómo se encuentran las intersecciones con el eje X?
-Para encontrar las intersecciones con el eje X, se iguala y a 0 y se resuelve la ecuación x^3 - 4x = 0.
¿Cuál es el primer paso al factorizar la ecuación x^3 - 4x = 0?
-El primer paso es observar que x es un factor común en todos los términos, por lo que se factoriza como x(x^2 - 4).
¿Cómo se aplica la diferencia de cuadrados en la ecuación?
-La diferencia de cuadrados se aplica en el término x^2 - 4, que se factoriza como (x - 2)(x + 2).
¿Cuáles son los factores que resultan de la factorización completa de la ecuación?
-Los factores resultantes son x, (x - 2) y (x + 2).
¿Qué valores de x se obtienen al igualar cada factor a 0?
-Al igualar cada factor a 0, se obtienen los valores x = 0, x = 2 y x = -2.
¿Cuáles son las intersecciones con el eje X para la función dada?
-Las intersecciones con el eje X son (-2, 0), (2, 0) y (0, 0).
¿Cómo se encuentran las intersecciones con el eje Y?
-Para encontrar las intersecciones con el eje Y, se iguala x a 0 y se resuelve la ecuación y = 0.
¿Cuál es el resultado de la ecuación y = x^3 - 4x cuando x = 0?
-Cuando x = 0, la ecuación se simplifica a y = 0^3 - 4*0, lo que resulta en y = 0.
¿Cuál es la intersección con el eje Y para la función dada?
-La intersección con el eje Y es (0, 0).
¿Cómo se representa gráficamente la función y = x^3 - 4x con sus intersecciones?
-La función se representa gráficamente con los puntos de intersección (-2, 0), (2, 0) y (0, 0), y una curva que pasa por estos puntos.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频
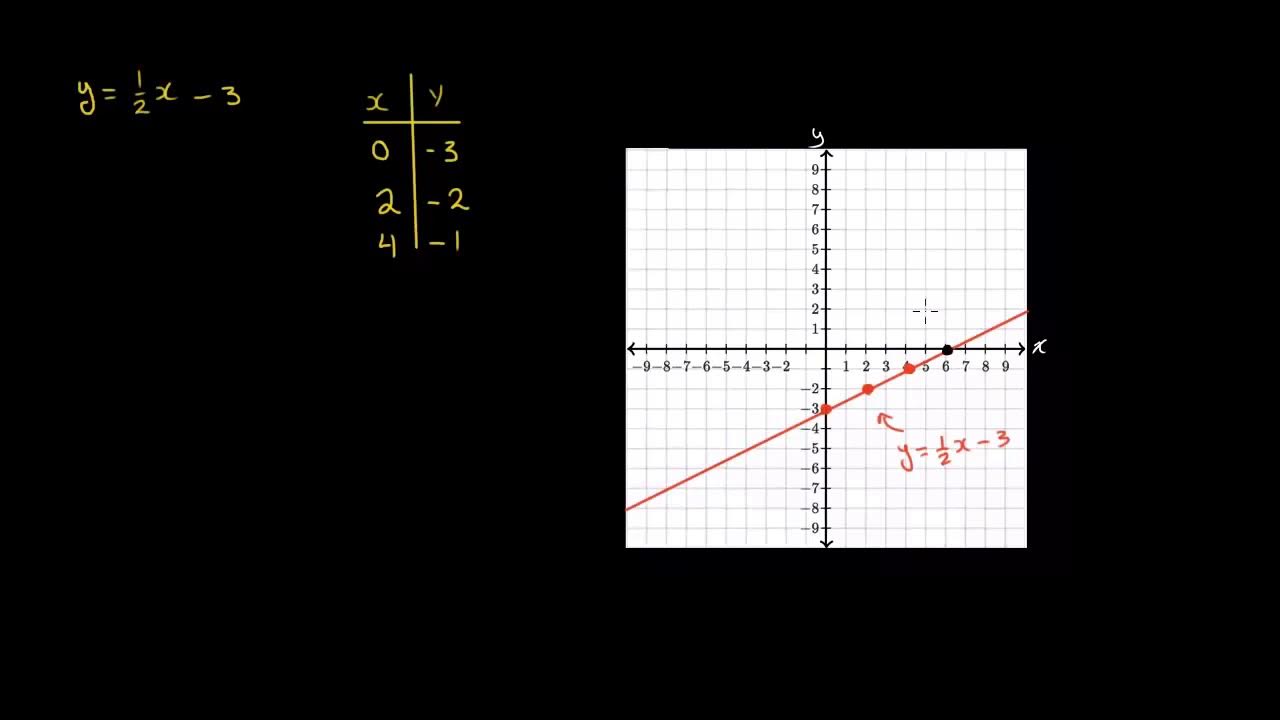
Introducción a las intersecciones con los ejes

Como graficar funciones racionales | Precálculo

Intersecciones de una función con los ejes X e Y / Función Lineal

PRIMER PROBLEMA FUNDAMENTAL GEOMETRÍA ANALÍTICA

Intersecciones con los ejes X y Y de una función cuadrática | puntos de corte con los ejes

Función Racional - Ejercicios Nivel 1 - Introducción
5.0 / 5 (0 votes)
