SOLVING SYSYEM OF NONLINEAR EQUATIONS || PRECALCULUS
Summary
TLDRThis educational video tutorial delves into solving systems of non-linear equations using three primary methods: substitution, elimination, and graphing. The instructor meticulously demonstrates each technique, starting with the substitution method by solving equations like y = -x + 2 and x^2 + y = 2. The elimination method is showcased through examples, simplifying complex equations to find solutions. Lastly, the graphing method is introduced, illustrating how to graphically solve systems and understand their intersections. The video is a comprehensive guide for learners seeking to master non-linear equation systems, complete with practical examples and clear explanations.
Takeaways
- 📘 The video lesson focuses on solving systems of non-linear equations using various methods.
- 🔍 The substitution method is demonstrated by solving an example where y is expressed in terms of x, and then substituted into another equation.
- 📐 The elimination method is explained through an example where terms are eliminated to find a solution for y, and then x is solved by substitution.
- 📊 The graphing method is introduced as a way to visualize and solve systems of equations by plotting them on a graph.
- 🧩 The video provides a step-by-step guide on how to apply each method, including factoring and solving for variables.
- 📉 The lesson includes examples of solving systems of equations that result in quadratic and linear equations.
- 🔢 The video demonstrates how to simplify equations by combining like terms and factoring out common factors.
- 📈 The process of converting non-linear equations into standard form, such as circles and ellipses, is explained to facilitate graphing.
- 📍 The video highlights the importance of identifying the centers and radii of circles and ellipses when graphing.
- 🎯 The lesson concludes with a summary of the methods taught and an encouragement to practice these techniques for better understanding.
Q & A
What are the three methods discussed in the video for solving systems of non-linear equations?
-The video discusses the substitution method, elimination method, and graphing method for solving systems of non-linear equations.
How does the substitution method work in solving a system of non-linear equations?
-The substitution method involves expressing one variable in terms of another from one equation and substituting it into the other equation to solve for the remaining variable.
Can you provide an example of a system of non-linear equations solved using the substitution method in the video?
-Yes, the example given is y = -x + 2 and x^2 + y = 2. By substituting y from the first equation into the second, the video solves for x and y.
What is the elimination method and how is it used to solve systems of non-linear equations?
-The elimination method involves manipulating the equations to eliminate one variable by adding or subtracting the equations, allowing the solution of the remaining variable.
Can you explain the graphing method mentioned in the video for solving systems of non-linear equations?
-The graphing method involves plotting the equations on a graph and finding the intersection points, which represent the solutions to the system of equations.
What is the significance of the equation x^2 - x = 0 in the context of the video?
-The equation x^2 - x = 0 is derived from a substitution process in the video, and it is factored to find the values of x that satisfy the system of equations.
How does the video handle the example where x^2 + y^2 = 10 and x - 3y = -10?
-The video substitutes x = 3y - 10 into the first equation, simplifies, and then solves for y, followed by substituting y back to find x, resulting in the solution (-1, 3).
What is the process for solving the system of equations x^2 - 6x + y^2 + 2y = 15 and x^2 - 6x - 2y = 3 using the elimination method?
-The video adds the two equations to eliminate x terms, simplifies to find a new equation in y, solves for y, and then substitutes y back into one of the original equations to solve for x.
How does the video approach the system of equations x^2 + y^2 - 6x - 2y = 6 and x^2 + 4y^2 - 6x - 8y = 51?
-The video transforms both equations into standard form to identify them as a circle and an ellipse, then uses graphing to find the intersection points.
What are the coordinates of the center of the circle and the ellipse given in the video?
-The center of the circle is at (3, 1), and the center of the ellipse is also at (3, 1), with the video indicating the ellipse is shifted diagonally by 4 units.
What is the final advice given by the video for learning more about solving systems of non-linear equations?
-The video encourages viewers to like, subscribe, and hit the bell button for more video tutorials on the subject.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频

Kurikulum Merdeka Matematika Kelas 9 Bab 1 Sistem Persamaan Linear Dua Variabel

Matematika kelas X - Sistem Persamaan Linear part 1 - Sistem Persamaan Linear Dua Variabel (SPLDV)
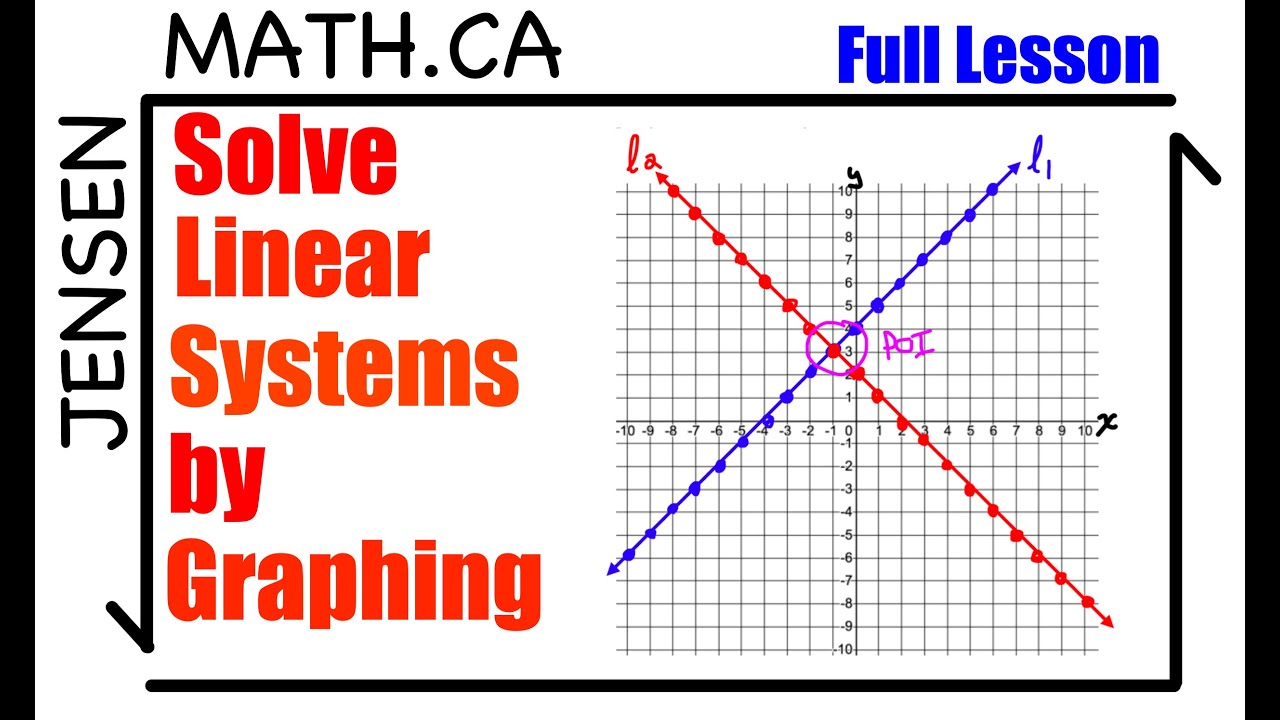
Solve a Linear System by Graphing | jensenmath.ca | grade 10

SPLDV (Substitusi, Eliminasi, Campuran)
Linear equations Gaussian Methods - English

Solving Systems of Equations in Two Variables
5.0 / 5 (0 votes)
