APLICACIONES DE LA INTEGRAL INDEFINIDA A LA ECONOMIA Y ADMINISTRACION-COSTO-PROBLEMA RES
Summary
TLDREl guion del video trata sobre el cálculo de la función de costo total y el costo promedio en economía. Se introduce la función de costo marginal como la derivada de una función de producción dada. El costo fijo es de 65, y se resuelve la integral de la función marginal para encontrar la función de costo total. Posteriormente, se calcula el valor de la constante de integración usando el costo fijo. Finalmente, se divide la función de costo total entre la cantidad producida para obtener el costo promedio por unidad, proporcionando una explicación clara y didáctica del proceso.
Takeaways
- 📚 El guion trata sobre el cálculo de la función de costo marginal y total en economía.
- 📉 La función de costo marginal es la derivada de la función de producción dada.
- 🔢 La función de producción mencionada es y = a^2 + 60x - 5x^3.
- 💰 El costo fijo es de 65, lo que significa que es el costo total cuando la producción x es cero.
- 📝 Se realiza la integración de la función de costo marginal para encontrar la función de costo total.
- 🧮 Al integrar, se aplican las reglas de integración de funciones polinómicas.
- 🔍 Se determina el valor de la constante de integración utilizando el costo fijo cuando x = 0.
- 📉 La función de costo total resultante es y = 2x + 30x^2 - (5/3)x^3 + 65.
- 🌀 Para encontrar el costo promedio, se divide la función de costo total por la cantidad producida x.
- ✂️ Al simplificar, se obtiene la función de costo promedio por unidad de producción.
- 📈 El guion ilustra el proceso de resolución paso a paso, enfocándose en la aplicación de conceptos matemáticos a problemas económicos.
Q & A
¿Cuál es la función de costo marginal mencionada en el guion?
-La función de costo marginal es la derivada de y con respecto a x, que es igual a 2 + 60x - 5x^2.
¿Qué significa el costo fijo en el contexto del guion?
-El costo fijo se refiere al costo total cuando la producción (x) es igual a 0, que en este caso es de 65.
¿Cómo se calcula el costo total a partir de la función de costo marginal?
-Para calcular el costo total, se integra la función de costo marginal con respecto a x, sumando el costo fijo al resultado.
¿Cuál es la integral de la función de costo marginal que se utiliza para calcular el costo total?
-La integral es la suma de las integrales de cada término: 2x, 30x^2, y -(5/3)x^3, más el costo fijo de 65.
¿Cómo se determina el valor de la constante de integración en la función de costo total?
-El valor de la constante de integración se determina al reemplazar y con 65 cuando x es igual a 0.
¿Cuál es la función de costo total que se obtiene tras integrar la función de costo marginal?
-La función de costo total es y = 2x + 30x^2 - (5/3)x^3 + 65.
¿Qué es el costo promedio y cómo se calcula?
-El costo promedio es el costo total dividido por la cantidad producida (x). Se calcula dividiendo la función de costo total entre x.
¿Cómo se expresa la función de costo promedio en el guion?
-La función de costo promedio se expresa como (2x + 30x^2 - (5/3)x^3 + 65) / x.
¿Qué pasos se siguen para resolver el problema del guion?
-Primero se identifica la función de costo marginal, luego se integra para obtener el costo total, se determina la constante de integración, y finalmente se calcula el costo promedio dividiendo el costo total entre x.
¿Por qué es importante el costo fijo al calcular el costo total?
-El costo fijo es importante porque representa los costos que no varían con la producción y deben ser incluidos en el cálculo total para obtener una visión completa de los costos.
¿Cómo se relaciona el costo marginal con el costo total?
-El costo marginal es la tasa de cambio del costo total con respecto a la producción adicional, y ayuda a determinar cómo varía el costo total a medida que aumenta la producción.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
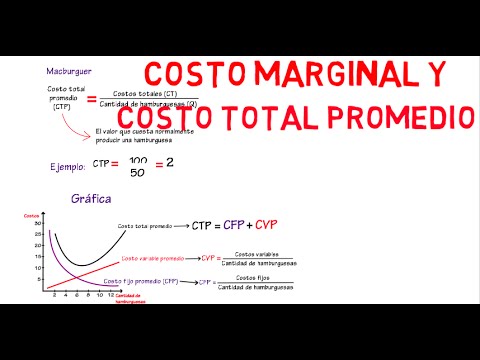
Costo marginal, costo total promedio | Cap. 16 - Microeconomía

MARGINAL COST and AVERAGE TOTAL COST - Explained for beginners!

3 minutos sobre | TEORÍA DE LA UTILIDAD MARGINAL

Método de Aproximación de Vogel

Qué es el WACC (CPPC) y cómo se calcula - Finanzas corporativas - Explicado para principiantes!

Aplicación de funciones matemáticas en la vida cotidiana.
5.0 / 5 (0 votes)
