Active Low Pass Filter - EXPERIMENT

Summary

This video tutorial demonstrates the operation of an active low-pass filter, which allows signals below a certain frequency to pass through. The presenter uses a circuit with an operational amplifier (op-amp) in inverting mode, with R2 and C components to create the filter. The critical frequency formula is provided as 1/(2πR2C). The video includes a practical setup, input signal testing at various frequencies, and a visual comparison of the input and output signals. The presenter also discusses the Butterworth filter characteristics and the expected gain at the cutoff frequency, concluding with a graph plotting the gain versus frequency to verify the filter's performance.

Takeaways

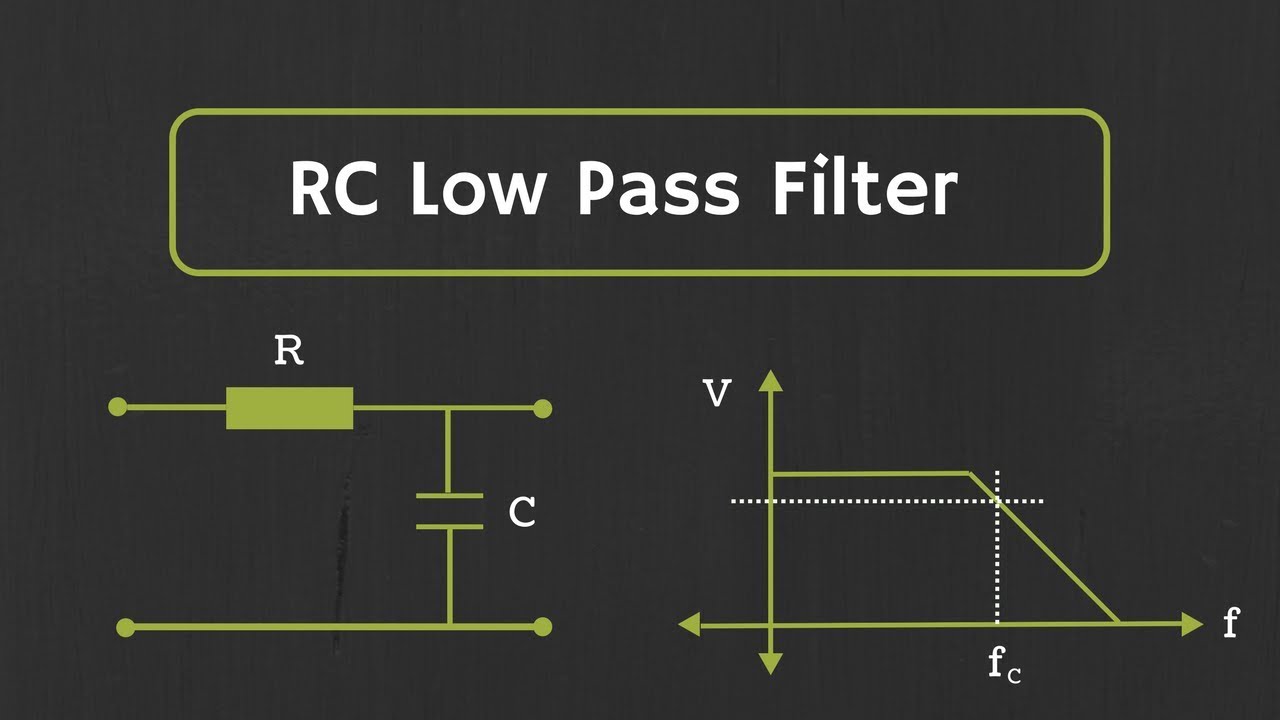
• 🎛️ The video demonstrates the working of an active low-pass filter, which only allows signals with frequencies lower than a certain cutoff frequency to pass through.
• 🔌 The active low-pass filter in the video uses an operational amplifier (op-amp) in an inverting configuration.
• 🛠️ The circuit shown uses a 741 C operational amplifier IC, with the input signal given through the inverting terminal (pin 2).
• 🧮 The formula for the cutoff frequency (critical frequency) of an active low-pass filter is given by 1 / (2πR2C).
• 📊 The video discusses the characteristics of a first-order active low-pass filter, also known as a Butterworth filter.
• 📉 The Butterworth filter has a flat response in the passband and falls off at a rate of 20 dB per decade after the cutoff frequency.
• 🔍 At the cutoff frequency, the gain is approximately -3 dB, which corresponds to about 70.7% of the input voltage.
• 🔄 The video shows a practical demonstration, where the input signal is compared to the output signal using a digital storage oscilloscope (DSO).
• 🔧 The experiment involves varying the input frequency and measuring the corresponding output signal to plot a gain vs. frequency graph.
• 📈 The video emphasizes the importance of taking multiple readings at different frequencies to get a smooth and accurate gain vs. frequency curve.

Q & A

What is the primary function of a low pass filter?

A low pass filter allows signals with frequencies lower than a certain critical frequency to pass through while blocking higher frequencies.

What distinguishes an active low pass filter from a passive one?

An active low pass filter contains active components such as an operational amplifier, which amplifies the input signal, in contrast to a passive filter that does not use active components.

What is the significance of the operational amplifier being used in inverting mode in the given circuit?

The operational amplifier in inverting mode inverts the phase of the input signal, which is a characteristic of the active low pass filter design demonstrated in the script.

What is the formula for calculating the critical or cutoff frequency of an active low pass filter?

The formula for calculating the cutoff frequency is \( \frac{1}{2\pi R_2C} \), where \( R_2 \) is the resistance and \( C \) is the capacitance in the filter circuit.

What type of filter is the demonstrated circuit known as, and what are its characteristics?

The demonstrated circuit is known as a first-order active low pass filter or Butterworth filter, characterized by a flat response region and a roll-off rate of 20 decibels per decade after the cutoff frequency.

At what frequency does the gain of the filter drop to about minus 3 decibels?

The gain of the filter drops to about minus 3 decibels at the cutoff frequency.

What is the practical significance of the cutoff frequency in the context of the experiment?

The cutoff frequency is the point at which the filter's output voltage is approximately 70.7% of the input voltage, marking the transition from the passband to the stopband.

What are the values of R2 and C used in the circuit for the experiment?

The R2 resistance used in the circuit is 1 kilo-ohm, and the capacitance C is 0.01 microfarads.

How does the output voltage of the filter change as the input frequency increases beyond the cutoff frequency?

As the input frequency increases beyond the cutoff frequency, the output voltage decreases, indicating the filter's effectiveness in attenuating higher frequencies.

What is the recommended approach for verifying the performance of the active low pass filter?

The recommended approach is to take multiple readings of the output voltage at various frequencies, both below and above the cutoff frequency, and then plot the gain versus frequency or output voltage versus frequency to verify the filter's performance.

How can viewers with questions or doubts about the experiment get assistance?

Viewers can leave their questions or doubts in the comment section of the video, and the presenter will get back to them.