RAZON DE CAMBIO PROMEDIO DE UNA FUNCION. Explicación Detallada Paso a Paso

Summary

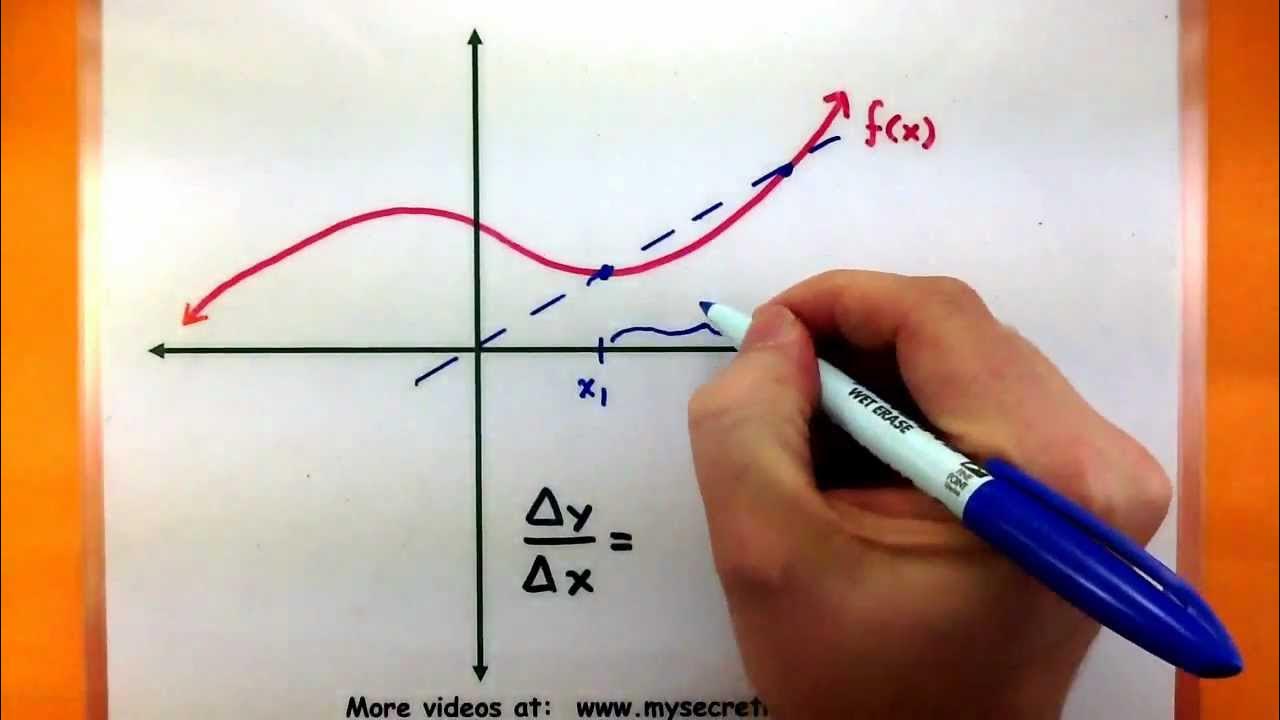
In this video, the concept of the *average rate of change* of a function is introduced. The average rate of change measures how much a function's output changes relative to its input over a given interval. Using a simple formula, the video explains how to calculate this by finding the difference in both the dependent and independent variables. The video concludes by hinting at the connection between the average rate of change and the concept of derivatives, setting the stage for more advanced calculus concepts in future lessons.

The video is abnormal, and we are working hard to fix it.
Please replace the link and try again.

Q & A

What is the main topic of the video?

The main topic of the video is the average rate of change of a function, an important concept before studying derivatives in calculus.

What does the average rate of change of a function represent?

The average rate of change of a function represents how the output (y or f(x)) changes in relation to the input (x) between two specific points on the function.

How is the change in the variable x denoted?

The change in the variable x is denoted by Δx, which represents the difference between two values of x, specifically x2 - x1.

What is the symbol Δ and what does it represent?

The symbol Δ (delta) represents a change or increment in a variable. In this case, Δx represents the change in x, and Δy (or Δf(x)) represents the change in y or the function's output.

How can the average rate of change be expressed mathematically?

The average rate of change can be expressed as the ratio of the change in the function’s output (Δy or Δf(x)) to the change in the input variable (Δx), i.e., (f(x2) - f(x1)) / (x2 - x1).

What is the relationship between the increment of x and the increment of y?

The increment of x (Δx) refers to the change in the independent variable, while the increment of y (Δy or Δf(x)) refers to the change in the dependent variable. Both increments are calculated as the difference between the two corresponding values.

Why is the average rate of change referred to as a ratio?

The average rate of change is referred to as a ratio because it compares the change in the function’s output (Δy or Δf(x)) to the change in the input variable (Δx), much like how velocity compares distance to time.

How can we calculate the increment of x?

The increment of x can be calculated by subtracting x1 from x2, i.e., Δx = x2 - x1.

What happens if you subtract x1 from itself?

If you subtract x1 from itself (x1 - x1), the result is 0, meaning there is no change in x.

What does the formula for the average rate of change represent geometrically?

Geometrically, the formula for the average rate of change represents the slope of the secant line between two points (x1, f(x1)) and (x2, f(x2)) on the graph of the function.