What are Radians? | Radian (Unit of Plane Angle) | Infinity Learn

Summary

This video explains the concept of radians as a logical way to measure angles in relation to the radius of a circle. It starts by contrasting degrees with radians and walks through the process of converting between the two. The video also explores the relationship between radians and the circumference of a circle, showing that one full rotation equals 2π radians, which is equivalent to 360°. Key conversions like π radians = 180° and π/2 radians = 90° are derived, along with the crucial fact that one radian is approximately 57.3°. The video makes radians more accessible and connects them to real-world geometry.

Takeaways

• 😀 Angles are typically measured in degrees, where a full rotation is 360°, a right angle is 90°, and a straight line is 180°.
• 😀 The measurement of angles in degrees is somewhat arbitrary and relates to the base 60 number system.
• 😀 Radians provide a more logical way to measure angles by relating the angle to the radius of a circle.
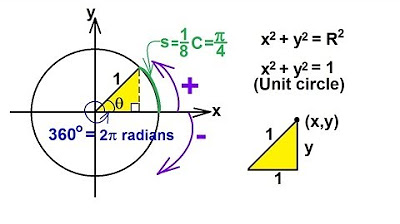
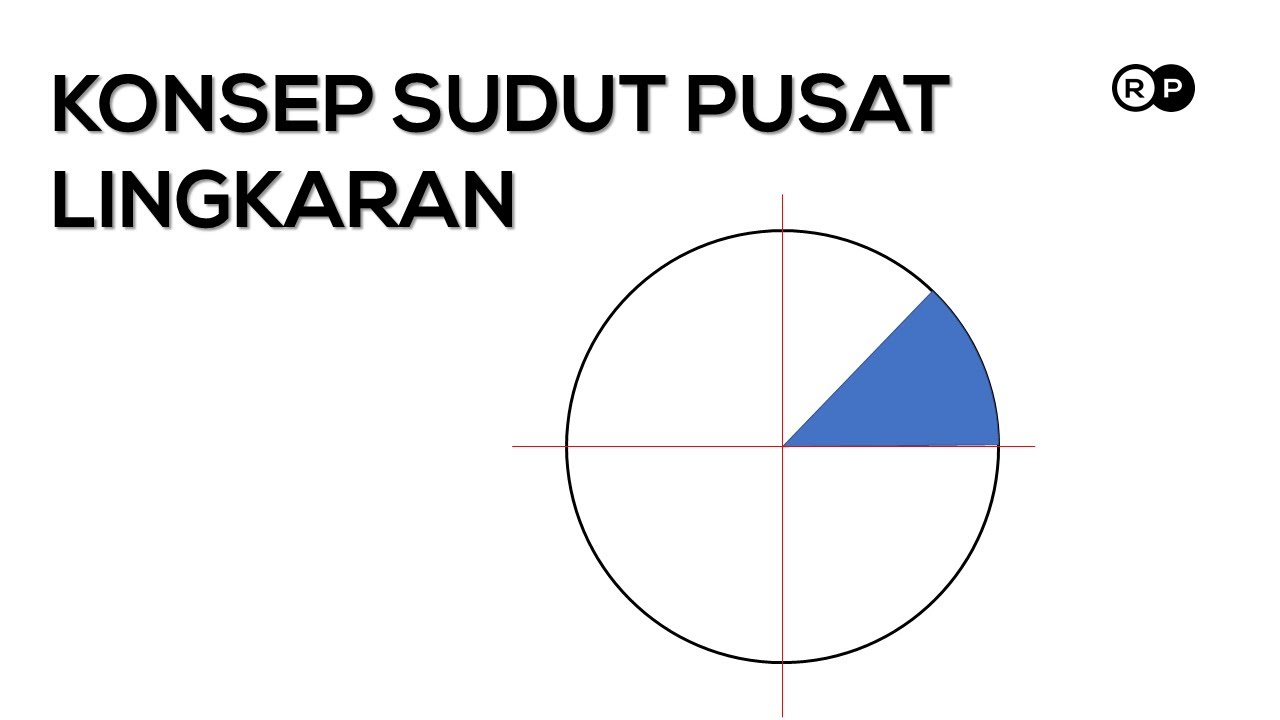
• 😀 One radian is defined as the angle subtended at the center of a circle by an arc whose length is equal to the radius of the circle.
• 😀 The concept of radians revolves around the idea that the angle is directly related to the circle’s radius.
• 😀 Radians are more intuitive in mathematics because they tie directly to the circle's geometry, with the radius appearing in the formula.
• 😀 To convert between degrees and radians, the key relationship is that 360° equals 2π radians.
• 😀 One full rotation (360°) equals 2π radians, and understanding this conversion is crucial for working with both units.
• 😀 Half a rotation (180°) equals π radians, and a right angle (90°) equals π/2 radians.
• 😀 The exact conversion formula for one radian in degrees is approximately 57.3°, derived from the ratio 360°/2π.
• 😀 Knowing one of the conversion relationships (like 360° = 2π radians) allows us to derive the others easily without memorizing them all.

Q & A

What is the main concept of radians?

Radians are a way of measuring angles based on the radius of a circle. When the length of an arc on the circle equals the radius, the angle formed is one radian.

Why is the number 360 used to measure angles in degrees?

The number 360 is somewhat arbitrary, but it is historically linked to the base-60 number system, which was used by ancient civilizations like the Babylonians.

How is a radian defined geometrically?

A radian is defined as the angle subtended at the center of a circle when the length of the arc equals the radius of the circle.

What is the relationship between degrees and radians?

The full rotation of a circle equals 360° or 2π radians. This means 360° equals 2π radians, establishing the conversion factor between the two units.

How many radians are in 180°?

180° is equal to π radians. This can be derived by dividing the 360° = 2π radians equation by 2.

What is the radian equivalent of a right angle?

A right angle, which is 90°, is equivalent to π/2 radians.

What would 2π radians represent in degrees?

2π radians is equal to 360°, representing one complete rotation around the circle.

What is the value of one radian in degrees?

One radian is approximately equal to 57.3° when π is approximated as 3.14.

How do you convert from radians to degrees?

To convert from radians to degrees, multiply the radian value by 180/π.

Why are radians considered a more logical way to measure angles than degrees?

Radians are based on the radius of the circle, making them a more natural measurement since the angle is directly related to the geometry of the circle itself.