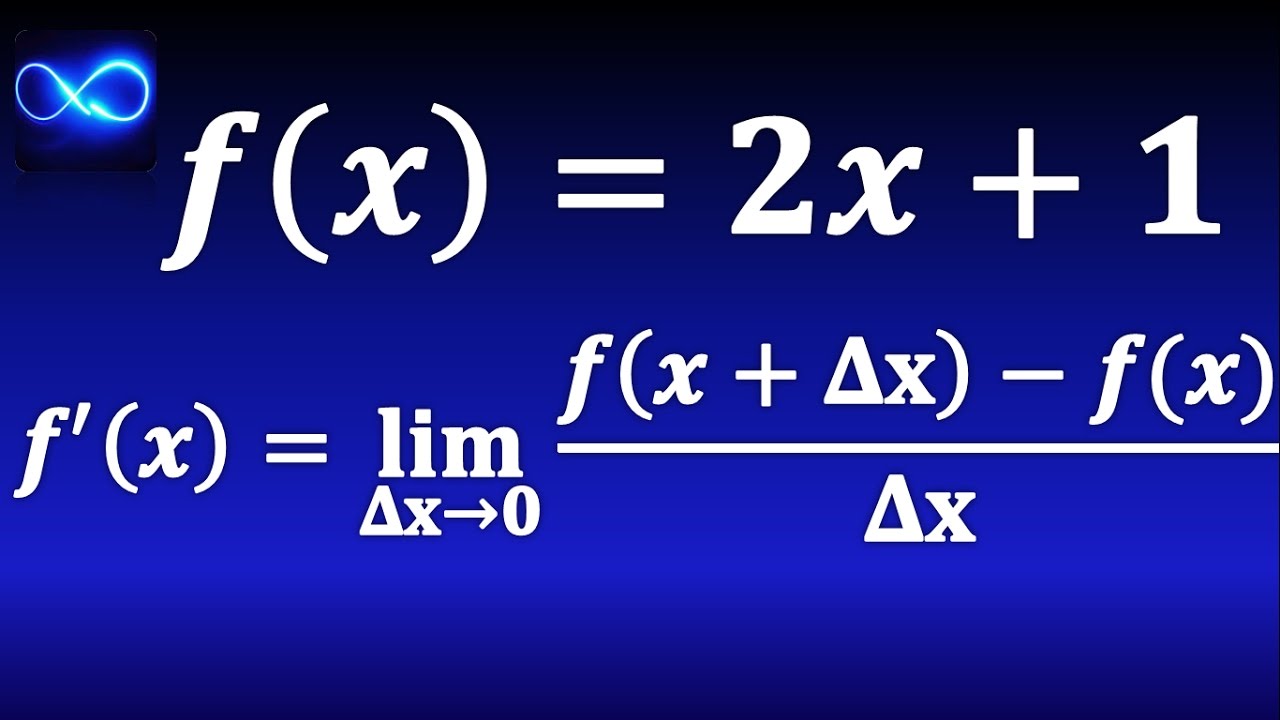Episode 3: Bahas Turunan Lengkap dengan Visualisasi

Summary

This video provides a comprehensive introduction to derivatives, starting with the formal definition as a limit and illustrating it with the function f(x) = x². It traces the historical origin of derivatives from tangent line problems, explains how secant lines approach tangents, and demonstrates calculating slopes and tangent line equations. The video clarifies the meaning of derivatives as the slope of a curve at a point, explores positive, negative, and zero slopes, and highlights practical applications in physics, astronomy, economics, and technology. Finally, it emphasizes understanding the limit-based definition over rote memorization, showing how derivatives unify diverse real-world concepts like instantaneous velocity and growth rates.

Takeaways

• 😀 The derivative of a function f(x), denoted f'(x), is defined as the limit: f'(x) = lim(h→0) [(f(x+h) - f(x))/h].
• 😀 f'(x) represents a new function derived from the original function f(x), indicating the rate of change at any point x.
• 😀 To compute the derivative of f(x) = x², use the limit definition to get f'(x) = 2x.
• 😀 Evaluating the derivative at a specific point, like x = 3, gives f'(3) = 6, representing the slope of the tangent line at that point.
• 😀 The concept of derivatives originated from the ancient tangent line problem, seeking a line that matches the curve's direction at a point.
• 😀 Modern tangent lines are defined using secant lines: the slope approaches that of the tangent line as h → 0.
• 😀 The derivative at a point gives the slope of the tangent line: positive for upward, negative for downward, and zero for horizontal.
• 😀 The power rule provides a shortcut: d/dx (x^n) = n*x^(n-1), though it ultimately stems from the limit definition.
• 😀 Derivatives have broad applications: in physics for instantaneous velocity, in economics for marginal profit, in biology for growth rates, and in technology like GPS and cameras.
• 😀 Regardless of context, the derivative always represents the rate of change, with the specific interpretation depending on the field of application.
• 😀 The limit notation captures the approach toward a value as h → 0; it does not mean h is actually zero.
• 😀 Memorizing derivative formulas is practical, but understanding the underlying limit concept is essential for solving diverse problems.

Q & A

What is the formal definition of a derivative?

The derivative of a function f(x), denoted as f'(x), is defined as the limit of the difference quotient as h approaches 0: f'(x) = lim(h→0) [(f(x+h) - f(x)) / h], provided this limit exists.

How do you calculate the derivative of f(x) = x² using the definition?

Plug f(x) = x² into the limit definition: f'(x) = lim(h→0) [(x+h)² - x²] / h = lim(h→0) [2xh + h²]/h = lim(h→0) (2x + h) = 2x.

How can you find the derivative at a specific point, for example x = 3?

Two methods: 1) Substitute x = 3 into the definition of the derivative and take the limit: f'(3) = lim(h→0) [(3+h)² - 9]/h = 6. 2) Compute the general derivative f'(x) = 2x first, then substitute x = 3: f'(3) = 2*3 = 6.

What historical problem led mathematicians to develop the concept of derivatives?

The initial idea came from the tangent line problem around 200 BC, when mathematicians tried to define a tangent line for curves, starting with Euclid’s definition for circles.

What is a secant line and how does it relate to the tangent line?

A secant line intersects a curve at two or more points. By letting one point approach the other (h → 0), the secant line approaches the tangent line, and the slope of the tangent line is defined by the derivative.

How is the slope of a line calculated from two points?

Slope m = Δy / Δx, where Δy is the change in y-values and Δx is the change in x-values between the two points.

What is the equation of the tangent line to f(x) = x² at point P(3,9)?

First, find the slope: f'(3) = 6. Then use the point-slope form: y - 9 = 6(x - 3), which can also be simplified to y = 6x - 9.

What does the derivative represent in the context of a tangent line?

The derivative at a point represents the slope of the tangent line to the curve at that point. A positive derivative indicates the line rises, a negative derivative indicates it falls, and zero derivative means a horizontal tangent.

How does the concept of derivative apply to real-life contexts?

Derivatives are used to calculate instantaneous speed (velocity), growth rates, marginal profit, and changes in economic indicators, as well as in technology (GPS, speedometers) and astronomy (predicting planetary motion).

Why is memorization of derivative formulas common, and what is the key concept to remember?

Memorization is common because it simplifies calculations, but the key concept is understanding that the derivative is the limit of Δy/Δx as Δx → 0. Formulas like d/dx[x^n] = nx^(n-1) are shortcuts derived from this fundamental limit definition.

What happens if the derivative at a point does not exist?

If the limit does not exist at a point, a tangent line cannot be drawn there, or it may be a vertical tangent where the slope approaches infinity, which is considered undefined in the standard derivative definition.

How does the derivative function f'(x) relate to the original function f(x)?

The derivative function f'(x) gives the slope of the tangent line of f(x) at any point x. For example, if f(x) = x², then f'(x) = 2x gives the slope of the tangent line at each x.