[Aljabar Linier] 3.1 Vektor di R2 & R3 - Definisi dan Aritmatika
Summary
TLDRThe video explores vectors in R2 and R3, starting with definitions and arithmetic operations. It distinguishes between scalar and vector quantities, explaining how vectors have both magnitude and direction, unlike scalars which only have magnitude. The discussion includes vector components, vector addition, subtraction, and scalar multiplication, with examples in two and three-dimensional space. It also touches on right-handed and left-handed coordinate systems, vector norms, and the calculation of distances between points. The video provides mathematical formulas and geometric visualizations to explain vector concepts in detail.
Takeaways
- 📐 The lecture discusses vectors in R2 and R3, starting with basic concepts like scalars and vectors, and their differences.
- 🔢 Scalars are quantities with magnitude only, such as length, mass, and temperature, while vectors are quantities with both magnitude and direction, like velocity, acceleration, and force.
- 📍 Vectors are represented by arrows in geometric terms, with their direction and magnitude represented by coordinates in space relative to the origin.
- ✍️ The components of a vector in R2 are denoted as V1 and V2, and for R3, they are V1, V2, and V3, corresponding to the x, y, and z axes respectively.
- 🤝 The concept of right-handed and left-handed coordinate systems is introduced, explaining how to determine the orientation of the z-axis in 3D space.
- 🔄 Vector addition is explained as the process of adding one vector to another to form a resultant vector from the initial point of the first vector to the terminal point of the second.
- 🔢 The subtraction of vectors, represented as W - V, results in a vector from the terminal point of V to the terminal point of W.
- 📈 Scalar multiplication of vectors is discussed, where multiplying a vector by a scalar can either increase or decrease its magnitude and potentially change its direction.
- 🚀 The lecture touches on the concept of translating vectors so that their initial points are not at the origin, which can simplify complex problems.
- 🔍 The properties of vector arithmetic are outlined, including commutative, associative, and distributive laws, as well as the existence of a zero vector and additive inverses.
- 📏 The norm (or magnitude) of a vector is defined as the length of the vector, calculated using the Pythagorean theorem in the context of its components.
Q & A
What is the difference between a scalar and a vector?
-A scalar is a physical quantity that has only magnitude (e.g., length, mass, temperature), while a vector is a physical quantity that has both magnitude and direction (e.g., velocity, acceleration, force).
How is a vector represented geometrically in R2 and R3?
-A vector in R2 and R3 is geometrically represented as a directed line segment from the origin (0,0 in R2 or 0,0,0 in R3) to a point defined by its coordinates, such as (V1, V2) in R2 or (V1, V2, V3) in R3.
What does the term 'right-handed' coordinate system mean in 3D space?
-A 'right-handed' coordinate system means that when you curl your fingers of the right hand from the x-axis toward the y-axis, your thumb points in the direction of the positive z-axis. It is the convention used in most 3D space applications.
How is vector addition performed geometrically?
-In vector addition, the second vector is positioned such that its starting point coincides with the endpoint of the first vector. The resulting vector is then drawn from the origin to the endpoint of the second vector.
How is vector subtraction performed geometrically?
-In vector subtraction, W - V is represented as the vector from the endpoint of vector V to the endpoint of vector W. This gives a new vector in the direction from the end of V to the end of W.
What happens when a vector is multiplied by a scalar?
-Multiplying a vector by a scalar changes its magnitude. If the scalar is positive, the vector's direction remains the same; if negative, the direction reverses. The magnitude is scaled by the scalar value.
How do you compute the components of a vector that does not start at the origin?
-To compute the components of a vector that starts at a point P1 (X1, Y1, Z1) and ends at point P2 (X2, Y2, Z2), you subtract the coordinates of the starting point from the endpoint: the vector is (X2 - X1, Y2 - Y1, Z2 - Z1).
What is the concept of axis translation in vector geometry?
-Axis translation in vector geometry involves shifting the coordinate system so that the initial point of a vector coincides with the origin. This simplifies the calculations of vectors that do not originate at the origin.
What is the 'norm' of a vector, and how is it calculated?
-The norm of a vector is its length or magnitude. It is calculated as the square root of the sum of the squares of its components: for a vector (V1, V2), the norm is √(V1² + V2²); for (V1, V2, V3), it is √(V1² + V2² + V3²).
How can you calculate the distance between two points in space?
-The distance between two points P1 (X1, Y1, Z1) and P2 (X2, Y2, Z2) is the norm of the vector formed between them. It is calculated as √((X2 - X1)² + (Y2 - Y1)² + (Z2 - Z1)²).
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Konsep Dasar Vektor (Vektor Bagian 1) Matematika Peminatan Kelas 10 - m4thlab

Linear combinations and span | Vectors and spaces | Linear Algebra | Khan Academy

Vektor pada dimensi tiga | Vektor dimensi 3

Espacios de coordenadas reales
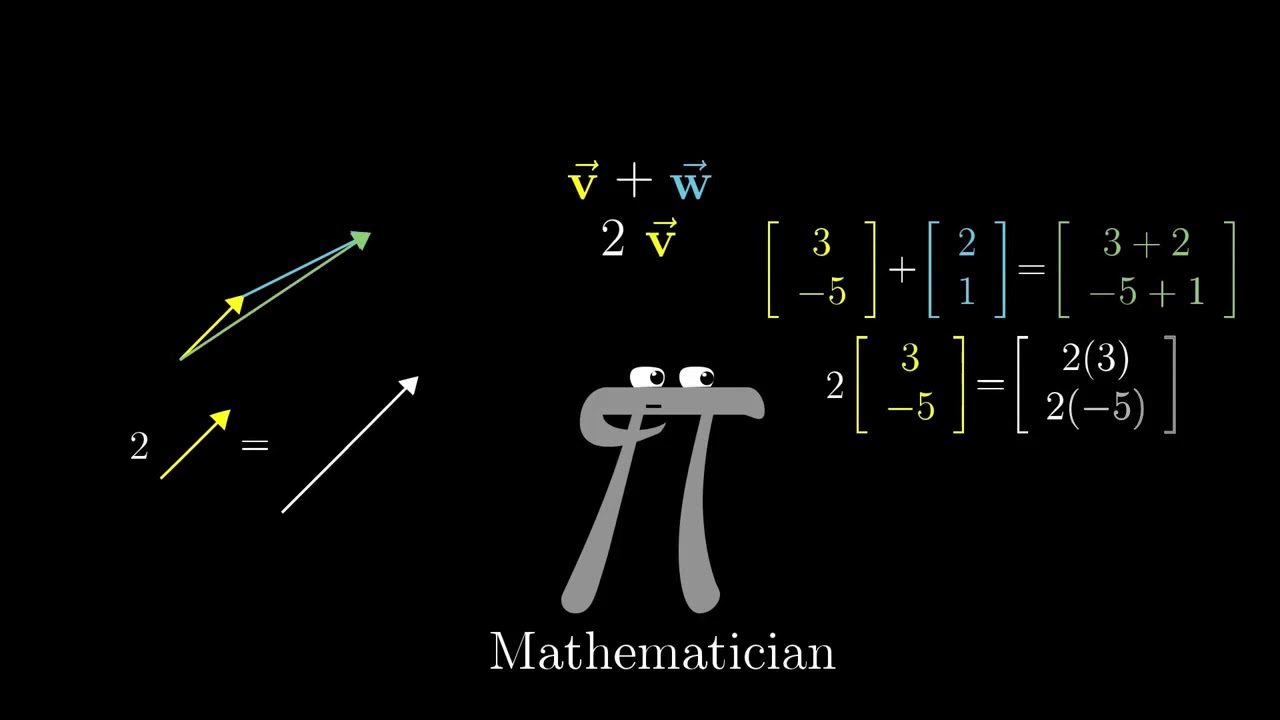
Что такое вектора? | Сущность Линейной Алгебры, глава 1

I Accidentally Bought the New Arduino UNO R4 (And It's INSANE)
5.0 / 5 (0 votes)