Dimensi 3 ( Prasyarat )

Summary

This video explores the concept of three-dimensional geometry, starting with the basics of dimensions and their relationships. It covers the historical contributions of Euclid, who defined points, lines, and flat shapes in geometry. The script explains the importance of diagonal planes and space diagonals, emphasizing their role in cubes and blocks. It introduces key formulas for calculating the length of diagonal planes and space diagonals. Additionally, the Pythagorean theorem is discussed, demonstrating its application in right triangles. The content is aimed at helping viewers understand and apply geometric concepts in three dimensions.

Takeaways

• 😀 Geometry is about shapes that have three dimensions: length, width, and height.
• 😀 Euclid, the father of geometry, identified zero dimensions as points, and one dimension as a line.
• 😀 Two dimensions involve flat shapes like rectangles, trapezoids, and kites.
• 😀 Three-dimensional shapes, like cubes and blocks, have length, width, and height.
• 😀 Diagonal planes connect two opposite corner points on the same plane, such as from point A to point C in a cube.
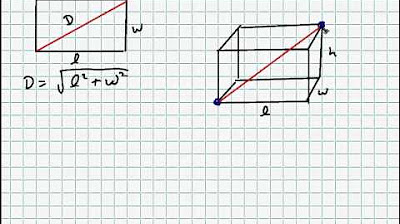
• 😀 Diagonal space refers to the line connecting two opposite corner points that are not on the same plane, like from point A to point G in a cube.
• 😀 A cube has 12 edges, and its diagonals can be calculated using Pythagoras' theorem.
• 😀 The diagonal of a plane in a cube is calculated using the formula: s√2, where 's' is the side length of the cube.
• 😀 For blocks, the diagonal calculations differ based on length, width, and height, using formulas like √(l² + b²).
• 😀 The Pythagorean theorem helps in finding the diagonal lengths in right-angled triangles, with the square of the hypotenuse equal to the sum of the squares of the adjacent sides.

Q & A

What are the three dimensions in geometry?

The three dimensions in geometry are length, width, and height, which define the space occupied by three-dimensional shapes like cubes and blocks.

Who is considered the father of geometry, and what did he contribute?

Euclid, who lived around 310 BC in Alexandria, is considered the father of geometry. He established fundamental concepts such as the definition of points (zero dimensions), lines (one dimension), and flat shapes (two dimensions).

What is the significance of a point in Euclidean geometry?

In Euclidean geometry, a point represents zero dimensions. It has no length, width, or height, and is the fundamental building block of geometric shapes.

What defines a two-dimensional shape?

A two-dimensional shape is a flat geometric figure that has only length and width. Examples include rectangles, trapezoids, and kites.

What is the difference between diagonal planes and diagonal spaces?

A diagonal plane connects two opposite corner points within the same plane, like the diagonal of a cube's side. In contrast, diagonal space connects two opposite corner points that are not in the same plane, such as the space diagonal in a cube.

What formula is used to calculate the diagonal of a plane in a cube?

The formula to calculate the diagonal of a plane in a cube is √2 * s, where s is the length of a side of the cube.

How is the diagonal of a space calculated?

The diagonal of space in a cube is calculated using the formula √(s² + s² + s²), which simplifies to √3 * s, where s is the length of a side of the cube.

How do the diagonal planes differ in a cube and a pyramid?

A cube has six diagonal planes, while an n-sided pyramid does not have any diagonal planes. The cube’s diagonal planes are formed by connecting opposite corner points within the same plane.

What is the Pythagorean theorem, and how is it applied in geometry?

The Pythagorean theorem states that in a right triangle, the square of the longest side (the hypotenuse) is equal to the sum of the squares of the two other sides. This relationship is expressed as c² = a² + b², where c is the hypotenuse and a and b are the legs of the triangle.

Why is it important to understand the difference between diagonal plane and space in geometry?

Understanding the difference between diagonal plane and space is crucial for calculating distances and measurements in three-dimensional shapes. It helps distinguish between measurements within the same plane and those that extend through the shape’s volume.