The Normal Distribution and the 68-95-99.7 Rule (5.2)

Summary

This video script explores the concept of the normal distribution, also known as the bell curve, and its characteristics, including the role of population parameters like mean (μ) and standard deviation (σ). It explains the 68-95-99.7 rule, which approximates the distribution's area within one, two, or three standard deviations from the mean. The script uses practical examples like exam scores and heights to illustrate these principles, offering viewers a clear understanding of how data clusters around the central value and the distribution's spread.

Takeaways

• 📚 A parameter is a number that describes a population, while a statistic describes a sample. For example, the population mean is denoted by the Greek letter mu (μ), and the sample mean by x-bar (𝑥̄).
• 📊 The normal distribution, also known as the bell curve, is a symmetrical density curve that shows data clustering around a central value, the population mean.
• 🌟 The position of the normal distribution on the number line is determined by the population mean (μ), while the spread is determined by the population standard deviation (Σ).
• 📉 The larger the standard deviation (Σ), the more spread out the normal distribution becomes, and the flatter the curve. Conversely, a smaller standard deviation results in a less spread out, taller curve.
• 🔍 The normal distribution is unimodal and symmetric, meaning it has a single peak and can be divided into two equal halves around the mean.
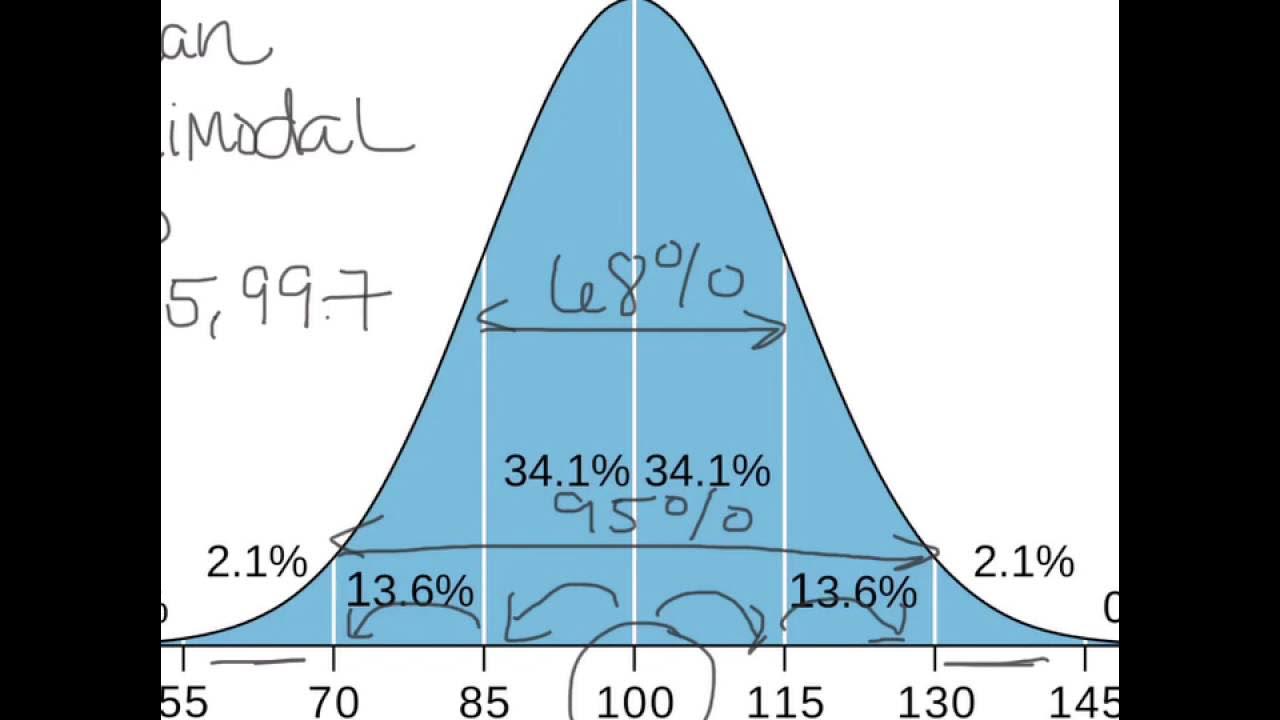
• 📈 The 68-95-99.7 rule states that approximately 68% of data falls within one standard deviation of the mean, 95% within two standard deviations, and 99.7% within three standard deviations.
• 🚫 A normal distribution never touches the x-axis, extending infinitely in both directions, but the area beyond three standard deviations becomes very small.
• 📐 The normal distribution's shape and spread are characterized by two parameters: the mean (μ) and the standard deviation (Σ), and it can be denoted as X ~ N(μ, Σ²).
• 📝 The 68-95-99.7 rule can be applied to any normal distribution to approximate the areas under the curve, regardless of its specific shape or size.
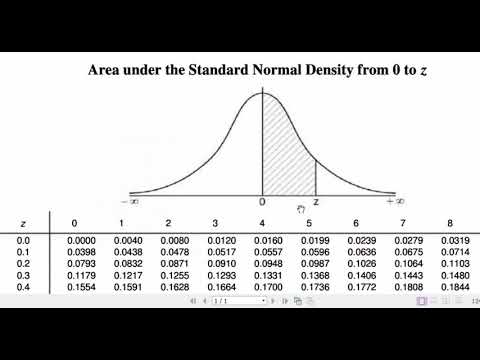
• 📑 The script provides examples and practice questions to illustrate the application of the normal distribution and the 68-95-99.7 rule in calculating areas under the curve.
• 💻 For further learning, the video suggests visiting the website simpleearningpower.com for study guides and practice questions related to the normal distribution.

Q & A

What is the difference between a parameter and a statistic?

A parameter is a number that describes data from a population, while a statistic is a number that describes data from a sample.

What symbols are used to represent the sample mean and sample standard deviation?

The sample mean is represented by x-bar (x̄) and the sample standard deviation is represented by s.

What symbols are used to represent the population mean and population standard deviation?

The population mean is represented by the Greek letter mu (μ) and the population standard deviation is represented by the Greek letter sigma (σ).

What is a normal distribution and why is it sometimes called the bell curve?

A normal distribution is a special type of density curve that is bell-shaped. It is called the bell curve because of its shape.

How does the population mean (mu) affect the position of the normal distribution?

The population mean (mu) determines the position of the normal distribution. If the mean increases, the curve shifts to the right; if the mean decreases, the curve shifts to the left.

How does the population standard deviation (sigma) affect the spread of the normal distribution?

The population standard deviation (sigma) determines the spread of the normal distribution. A larger standard deviation results in a more spread-out distribution, while a smaller standard deviation results in a less spread-out distribution.

What does the notation N(μ, σ) mean in the context of a normal distribution?

The notation N(μ, σ) indicates that the variable X follows a normal distribution with a mean of μ and a standard deviation of σ.

What does the 68-95-99.7 rule state?

The 68-95-99.7 rule states that in a normal distribution, approximately 68% of the data falls within one standard deviation of the mean, 95% falls within two standard deviations, and 99.7% falls within three standard deviations.

If the mean height of students at a university is 5.5 feet with a standard deviation of 0.5 feet, what percentage of students are between 5 and 6 feet tall?

Approximately 68% of students are between 5 and 6 feet tall, according to the 68-95-99.7 rule.

In a normal distribution with a mean of 70 and a standard deviation of 10, what is the approximate area contained between 70 and 90?

The approximate area contained between 70 and 90 is 47.5%, as it represents half of the area within two standard deviations (95%).

For a normal distribution with a mean of 0 and a standard deviation of 1, what is the approximate area contained between -2 and 1?

The approximate area contained between -2 and 1 is 81.5%, calculated by adding 47.5% (area from -2 to 0) and 34% (area from 0 to 1).