¿Cómo identificar a que tipo de fracciones parciales corresponde una integral?

Summary

En este video, el instructor enseña cómo resolver integrales utilizando fracciones parciales, cubriendo tres casos principales. El primer caso se refiere a fracciones con factores lineales no repetidos, el segundo a fracciones con denominadores de grado mayor que el numerador, y el tercero a fracciones donde el numerador es mayor que el denominador, lo que requiere una división algebraica previa. A lo largo del video, se muestran ejemplos prácticos de cómo factorizar y simplificar las expresiones, y cómo aplicar las reglas de integración de manera efectiva para resolver los ejercicios de fracciones parciales.

Takeaways

• 😀 En el video se explica cómo determinar el caso al que corresponde cada ejercicio, con enfoque en la comprensión antes de la resolución paso a paso.
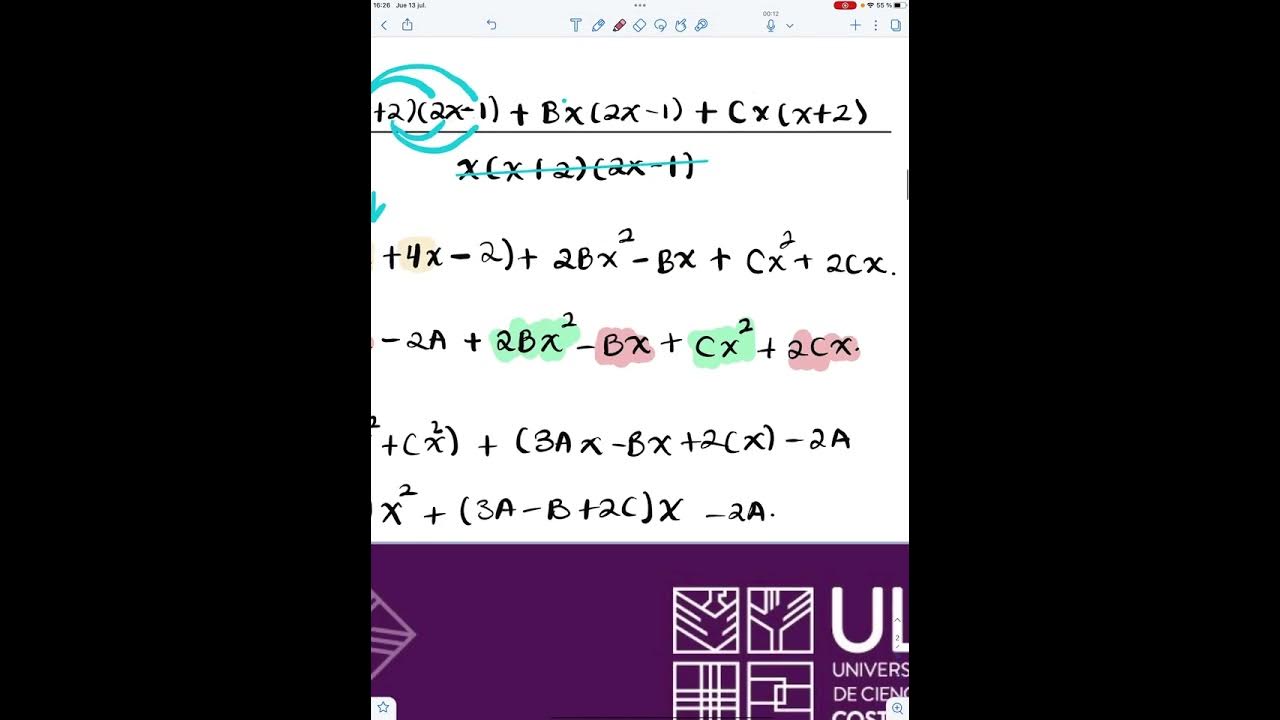
• 😀 En el primer caso, se identifica un ejercicio con factores lineales no repetidos mediante la factorización de un monomio y un trinomio.
• 😀 En el segundo caso, se analiza el grado del numerador y el denominador, donde el numerador tiene un grado menor que el denominador.
• 😀 El segundo ejercicio implica la factorización del denominador para simplificar la integral.
• 😀 El tercer ejercicio presenta una situación donde el grado del numerador es mayor que el del denominador, lo que requiere una división algebraica.
• 😀 En la división algebraica, es importante tener en cuenta los signos negativos, ya que afectan a los términos dentro de la operación.
• 😀 Cuando el numerador tiene un grado mayor, se realiza una división algebraica y se simplifica la expresión para hacerla más manejable.
• 😀 Después de realizar la división algebraica, se aplica fracciones parciales para descomponer la integral en partes más fáciles de resolver.
• 😀 El proceso de factorización es clave para determinar qué tipo de caso tiene cada ejercicio y facilitar la resolución de la integral.
• 😀 El video también resalta cómo manejar términos comunes al factorizar denominadores con factores repetidos, especialmente en el caso 2.
• 😀 Finalmente, se concluye que la integral de cada ejercicio puede resolverse mediante fracciones parciales después de simplificar adecuadamente.

Q & A

¿Qué se busca lograr en este video?

En este video, el objetivo principal es ayudar a los estudiantes a entender cómo identificar a qué caso corresponde cada ejercicio de fracciones parciales, sin resolver los ejercicios paso a paso, sino centrarse en comprender la estructura de cada uno.

¿Cómo se clasifica el primer ejercicio?

El primer ejercicio se clasifica como 'Caso 1', que corresponde a factores lineales no repetidos. Esto se debe a que el numerador y denominador fueron factorizados y el grado del numerador es menor que el del denominador.

¿Qué hace el hablante con respecto al denominador en el segundo ejercicio?

En el segundo ejercicio, el hablante observa que el grado del numerador es menor que el del denominador, por lo que se dedica a buscar los factores del denominador, que se puede factorizar por un término común.

¿Qué sucede cuando el grado del numerador es mayor que el del denominador?

Cuando el grado del numerador es mayor que el del denominador, el procedimiento a seguir es realizar una división algebraica. Esta es una técnica para simplificar la fracción antes de continuar con la descomposición en fracciones parciales.

¿Qué es la 'división algebraica' y por qué es importante?

La división algebraica es un proceso en el que se divide el numerador por el denominador, como en una división de polinomios, para simplificar la fracción antes de trabajar con fracciones parciales. Es importante porque permite reducir la fracción a una forma más manejable para la integración.

¿Cómo afecta el 'menos imaginario' durante la división algebraica?

El 'menos imaginario' en la división algebraica se utiliza para cambiar los signos de los términos, lo que afecta el resultado de la operación, transformando los términos positivos en negativos, lo cual es un paso necesario para el procedimiento correcto.

¿Qué se quiere lograr con la simplificación de los términos durante la división algebraica?

El objetivo de simplificar los términos durante la división algebraica es reducir la fracción a un formato más fácil de manejar, eliminando términos innecesarios y simplificando la expresión para hacer la integración más directa.

¿Qué tipo de casos se presentan en los ejercicios revisados?

Los ejercicios revisados corresponden principalmente al 'Caso 1' (factores lineales no repetidos) y al 'Caso 2' (factores lineales repetidos), dependiendo de la estructura del denominador y si el numerador tiene un grado mayor que el denominador.

¿Qué sucede con la fracción cuando se realiza una división algebraica correctamente?

Cuando se realiza una división algebraica correctamente, el resultado es una fracción simplificada que es más fácil de manejar en el contexto de fracciones parciales, permitiendo una integración más sencilla.

¿Por qué el hablante menciona que algunos términos son eliminados durante la división?

Los términos son eliminados porque, durante la división algebraica, los términos que resultan ser iguales o se cancelan entre sí no afectan el resultado final. Esto simplifica la expresión y facilita la resolución de la integral.