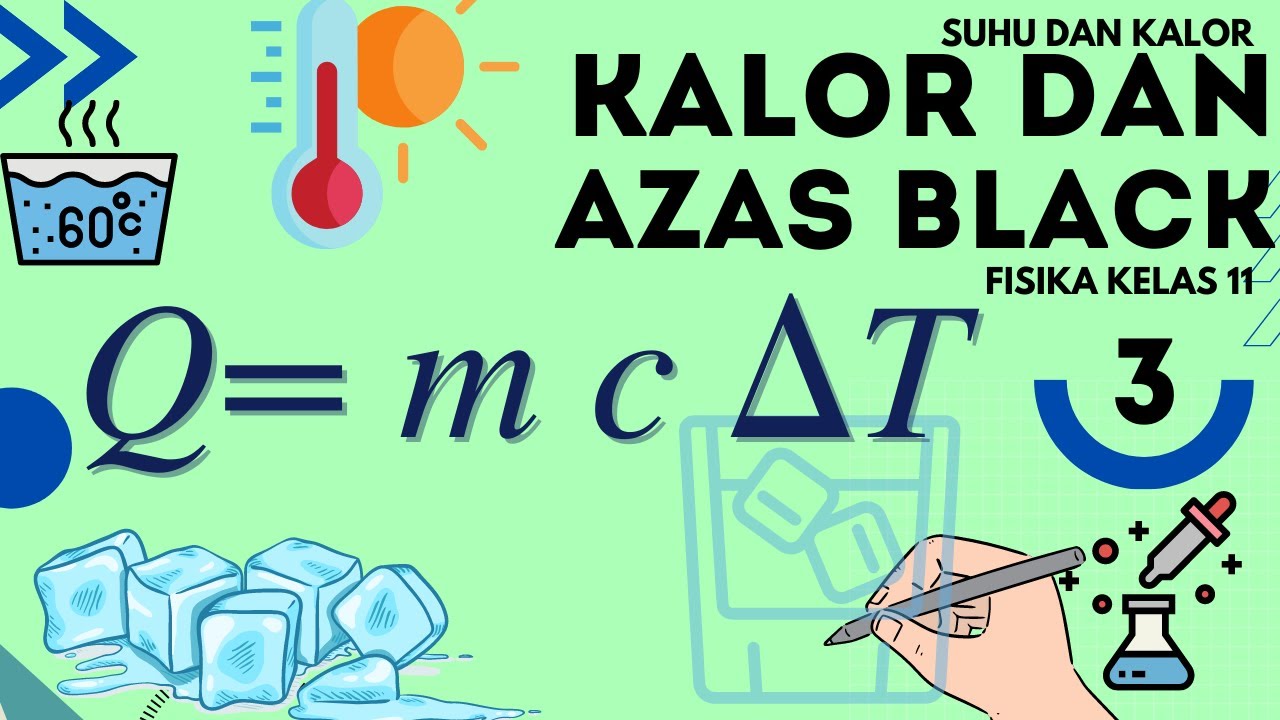Kalor dan Perpindahan Kalor • Part 2: Asas Black - Cara Menghitung Suhu Campuran

Summary

This video explains the concept of heat transfer and the principle of Black's Law, which states that the heat lost by a hotter object equals the heat gained by a cooler one. Through various examples, including the mixing of water at different temperatures and the interaction between ice and water, the video demonstrates how thermal equilibrium is reached. Viewers learn how to calculate heat exchange using formulas, and gain insight into how changes in temperature affect different substances, such as ice and water. The video provides step-by-step problem-solving to help viewers understand key calorimetry concepts.

Takeaways

• 😀 Black's principle states that when two substances of different temperatures are mixed, the amount of heat lost by the hotter substance equals the amount of heat gained by the cooler substance.
• 😀 Heat transfer occurs from the hotter substance to the cooler one until thermal equilibrium is reached, where both substances reach the same temperature.
• 😀 Thermal equilibrium is when two objects reach the same temperature, and no more heat transfer occurs between them.
• 😀 The formula used to calculate heat transfer involves the specific heat capacity, mass, and temperature change: Q = mcΔT.
• 😀 In the case of mixing two substances with the same phase, such as water at different temperatures, the heat lost by the hot water equals the heat gained by the cold water.
• 😀 The final temperature after mixing is determined by balancing the heat exchanged, considering the masses and specific heat capacities of the substances involved.
• 😀 In a scenario where ice and water are mixed, thermal equilibrium could occur at temperatures below or above 0°C, depending on the heat required to melt the ice.
• 😀 When ice is involved, the heat required for the ice to melt (latent heat of fusion) must be considered in the calculations of the final temperature.
• 😀 The specific heat capacity of water and ice, as well as the latent heat of fusion, plays a crucial role in determining the final temperature when mixing ice and water.
• 😀 In cases where not all the ice melts or not all the water evaporates, the equilibrium temperature will reflect the heat distribution between the substances involved, and some ice may remain unmelted or water may remain liquid.

Q & A

What does Black's principle state about heat exchange between two substances?

Black's principle states that the amount of heat released by a hotter substance is equal to the amount of heat absorbed by a cooler substance when they are mixed.

What is the term used to describe the point at which heat transfer stops between two substances?

The term used is 'thermal equilibrium,' which occurs when both substances reach the same temperature, stopping further heat exchange.

How do we calculate the final temperature when two substances with different temperatures are mixed?

We use the formula Q_lepas = Q_terima, where Q_lepas is the heat released by the hotter substance and Q_terima is the heat absorbed by the cooler substance. The formula involves the masses, specific heat capacities, and temperature changes of both substances.

In the first example, how do we calculate the final temperature of the water mixture?

The final temperature is calculated by applying the formula for heat transfer and solving for the temperature. After simplifying the equations, the final temperature is determined to be 42°C.

What happens in the second example, when ice and water are mixed?

In this example, heat transfer occurs between the ice and the water. The heat from the water raises the ice's temperature and melts it. We must consider the specific heat capacities of both ice and water, and the heat required to melt the ice.

How do we calculate the heat required to melt the ice in the second example?

The heat required to melt the ice is calculated by multiplying the mass of the ice by the heat of fusion of ice (80 cal/gram). This gives the total heat required to melt the ice.

What is the significance of thermal equilibrium in the second example with ice and water?

Thermal equilibrium determines whether the ice melts completely or only partially. If the heat released by the water is enough to melt the ice, the ice will fully melt. Otherwise, only a part of the ice will melt.

How do we handle the possibility of the final temperature being below 0°C in such heat transfer problems?

To handle this, we calculate the heat required to raise the ice to 0°C and the heat required to melt the ice. If the total heat provided by the water is greater than the total heat needed to bring the ice to 0°C and melt it, the equilibrium temperature will be above 0°C.

What is the key difference in the third example involving ice at its melting point?

The key difference is that not all of the ice melts. Instead, only a portion of the ice melts, and the temperature reaches 0°C. We calculate the amount of ice that melts by comparing the heat required to melt the ice with the heat released by the water.

How do you determine the mass of ice that melts in the third example?

To determine the mass of the ice that melts, we use the heat equation and solve for the mass of ice that can melt given the heat released by the water. In this case, 2.5 grams of ice melts.