Sistemas de ecuaciones lineales 2x2 | Método de Reducción - Eliminación | Introducción
Summary
TLDREn este video, se explica el método de reducción para resolver sistemas de ecuaciones 2x2. El instructor aborda cómo eliminar una de las variables mediante la igualación de los coeficientes con signos opuestos, utilizando multiplicaciones para modificar las ecuaciones. Se presentan ejemplos prácticos para ilustrar los pasos, desde el proceso básico hasta casos más complejos. El objetivo es que los estudiantes aprendan a manipular los sistemas de ecuaciones, obteniendo un sistema reducido a una sola ecuación. Además, se proporcionan ejercicios para practicar y fortalecer el aprendizaje.
Takeaways
- 😀 El método de reducción se utiliza para resolver sistemas de ecuaciones de 2x2 eliminando una variable mediante la manipulación de los coeficientes.
- 😀 El primer paso importante en este método es lograr que una de las variables tenga coeficientes opuestos en ambas ecuaciones.
- 😀 Al lograr coeficientes opuestos, se pueden sumar o restar las ecuaciones para eliminar una variable y obtener una única ecuación con una sola incógnita.
- 😀 Para eliminar una variable, se puede multiplicar una o ambas ecuaciones por un número que haga que los coeficientes sean opuestos entre sí.
- 😀 Es fundamental organizar las ecuaciones correctamente antes de intentar la eliminación, asegurándose de que los términos con las incógnitas estén a la izquierda y el número constante a la derecha.
- 😀 En algunos casos, cuando los coeficientes no permiten una eliminación directa, se debe multiplicar las ecuaciones por un valor que facilite la eliminación, incluso si esto resulta en fracciones.
- 😀 El uso de signos negativos es crucial para garantizar que las variables se eliminen correctamente durante el proceso de reducción.
- 😀 Para sistemas de ecuaciones complejos, se recomienda buscar el mínimo común múltiplo (MCM) de los coeficientes para facilitar la eliminación de variables.
- 😀 Las opciones de eliminación pueden variar, y es importante elegir la estrategia que mejor se ajuste al problema, ya sea multiplicando por valores positivos o negativos.
- 😀 Se alienta a los estudiantes a practicar con diferentes ejemplos para comprender mejor cómo aplicar el método de reducción y encontrar las soluciones de manera efectiva.
Q & A
¿Cuál es el primer paso en el método de reducción para resolver un sistema de ecuaciones de 2x2?
-El primer paso consiste en hacer que una de las variables (ya sea x o y) tenga el mismo coeficiente en ambas ecuaciones, pero con signos opuestos. Esto permite que la variable se elimine al sumar las ecuaciones.
¿Qué ocurre después de que las variables se eliminan en el segundo paso del método de reducción?
-En el segundo paso, después de que las variables se eliminan, se obtiene una sola ecuación con una sola incógnita, lo que facilita resolver para la variable restante.
¿Por qué es importante organizar las ecuaciones antes de empezar a resolverlas?
-Es crucial organizar las ecuaciones para asegurarse de que las variables (x y y) y los números estén en el orden correcto (x, y, igual a número), lo que facilita el proceso de eliminación y la solución del sistema.
¿Qué se debe hacer cuando los coeficientes de las ecuaciones no son fácilmente multiplicables entre sí para eliminar una variable?
-Cuando los coeficientes no son fácilmente multiplicables entre sí, se debe buscar el mínimo común múltiplo (MCM) de los números involucrados, para poder hacer que los coeficientes coincidan y luego eliminar una de las variables.
¿Cómo se debe proceder cuando los coeficientes de ambas ecuaciones son positivos?
-Cuando ambos coeficientes son positivos, se debe multiplicar una de las ecuaciones por un número negativo para que el signo de uno de los coeficientes cambie y así permitir la eliminación de la variable.
¿Por qué es importante multiplicar toda la ecuación cuando se decide multiplicar una ecuación por un número?
-Es importante multiplicar toda la ecuación porque si solo se multiplican algunos términos, el sistema pierde consistencia y no se podrá resolver correctamente.
¿Qué estrategia se utiliza cuando no se puede multiplicar un coeficiente por otro de forma sencilla?
-Cuando no se puede multiplicar un coeficiente de forma sencilla, se puede recurrir al uso del mínimo común múltiplo (MCM) para hacer coincidir los coeficientes y luego proceder con la eliminación de una variable.
En el caso de las fracciones, ¿cómo se maneja el proceso de eliminación?
-En el caso de las fracciones, se deben convertir en números enteros, si es necesario, multiplicando ambos lados de las ecuaciones por un común denominador para evitar trabajar con fracciones.
¿Qué sucede si se elige mal el número por el cual multiplicar las ecuaciones?
-Si se elige mal el número por el cual multiplicar las ecuaciones, el proceso de eliminación no funcionará correctamente y no se obtendrá el resultado esperado. Es importante hacer las multiplicaciones con cuidado y verificar los resultados.
¿Cómo se puede comprobar que el sistema de ecuaciones se resolvió correctamente?
-Se puede comprobar que el sistema se resolvió correctamente sustituyendo los valores obtenidos para las variables en las ecuaciones originales. Si ambas ecuaciones se cumplen, la solución es correcta.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Sistema de Ecuaciones 2x2 - Método de Eliminación o Reducción

COMO RESOLVER UN SISTEMAS DE ECUACIONES DE 2X3/METODO DE REDUCCION
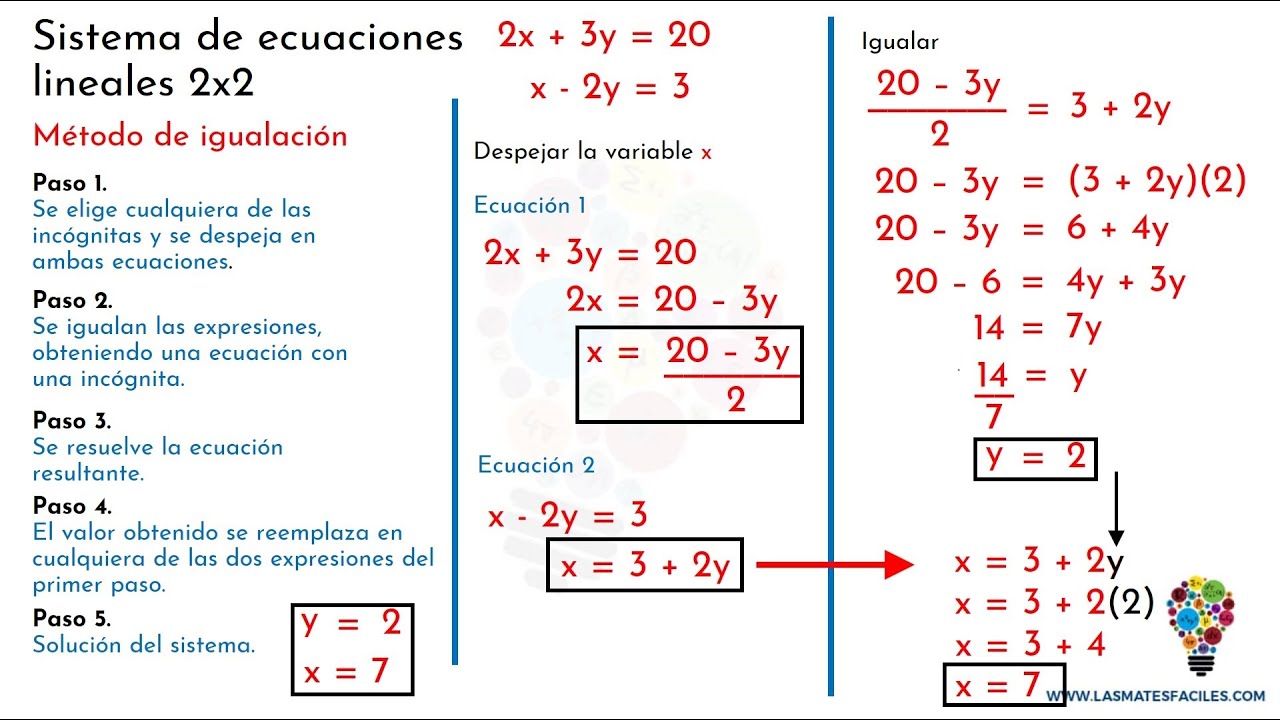
Sistemas de Ecuaciones 2x2 - Método de Igualación

Sistema de ecuaciones 2x2. Método de suma y resta.Álgebra

09. ¿Qué es un sistema de ecuaciones lineales con dos incógnitas?

RESOLVER SISTEMAS DE ECUACIONES MÉTODO DE REDUCCIÓN O SUMA Y RESTA Super fácil - Para principiantes
5.0 / 5 (0 votes)
