FISIKA KELAS XI - DEBIT DAN ASAS KONTINUITAS || FLUIDA DINAMIS

Summary

In this video, Yusuf Armada explains the concepts of dynamic fluids, focusing on fluid flow, flow rate, and the continuity equation. He introduces fluid dynamics with examples like water flowing through pipes and faucets. The flow rate (Q) is defined and calculated using the formula Q = A × v, demonstrating practical applications like filling a bucket. The principle of continuity is also discussed, showing how fluid velocity increases in narrower pipes. The video offers clear, step-by-step explanations, making complex topics accessible for students, while encouraging viewers to engage by liking, sharing, and subscribing.

Takeaways

• 😀 Dynamic fluids are fluids that are in motion, like water in rivers, taps, or pipes.
• 😀 Flow rate (Debit) is the amount of fluid flowing through a cross-sectional area per unit time, calculated by the formula Q = A × V.
• 😀 Flow rate can be used to calculate the time it takes to fill a container given the volume and flow rate of the fluid.
• 😀 The formula for flow rate is Q = A × V, where A is the cross-sectional area and V is the velocity of the fluid.
• 😀 When calculating the time required to fill a container, the volume of the container is divided by the flow rate.
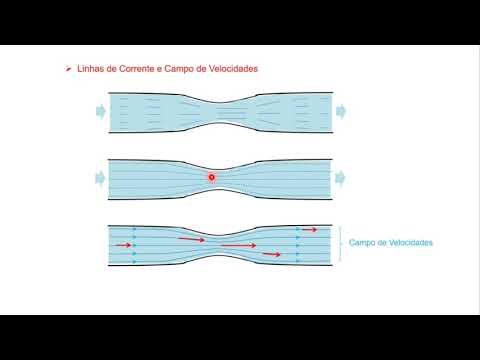
• 😀 The Continuity Principle states that the flow rate (Debit) is conserved along a streamline, meaning fluid entering and leaving a section must have the same flow rate.
• 😀 According to the Continuity Principle, when the cross-sectional area of a pipe decreases, the velocity of the fluid increases.
• 😀 The relationship between flow rate, area, and velocity is represented as A1 × V1 = A2 × V2.
• 😀 Example: In pipes with different diameters, water flows faster through narrower pipes and slower through wider pipes, maintaining the same flow rate.
• 😀 The Continuity Principle explains why squeezing the end of a hose causes the water to spray out faster.
• 😀 The video encourages viewers to engage with the content by liking, sharing, and subscribing, reinforcing the importance of understanding fluid dynamics.

Q & A

What is fluid dynamics?

Fluid dynamics refers to the study of fluids in motion. It specifically deals with the behavior of fluids such as water or air when they are in motion, for example, water flowing in a river or through a pipe.

What does 'debit aliran' (flow rate) mean in fluid dynamics?

'Debit aliran' or flow rate is a quantity that represents the volume of fluid passing through a cross-sectional area per unit of time. Mathematically, it is represented as Q = A * v, where A is the cross-sectional area, and v is the velocity of the fluid.

How is flow rate calculated?

Flow rate can be calculated using the formula Q = A * v, where Q is the flow rate (in cubic meters per second), A is the cross-sectional area through which the fluid flows, and v is the velocity of the fluid.

What is the unit of flow rate?

The unit of flow rate (Q) is cubic meters per second (m³/s), representing the volume of fluid passing through a certain area per second.

How can we calculate the time needed to fill a container with a given flow rate?

To calculate the time required to fill a container, use the formula time = volume / flow rate. In the example given, the volume of the container is 20 liters, and the flow rate was calculated as 2 x 10⁻³ m³/s, resulting in a time of 10 seconds.

What is the principle of continuity in fluid dynamics?

The principle of continuity, also known as the law of conservation of flow, states that the flow rate (debit) must remain constant throughout a pipe or any flow path. This means that if the area of the pipe changes, the velocity of the fluid will adjust to maintain the same flow rate.

What happens when the diameter of a pipe is reduced, according to the continuity principle?

When the diameter of a pipe is reduced, the velocity of the fluid increases to maintain the same flow rate. This is why when you pinch the end of a garden hose, the water comes out faster.

How does the continuity principle apply to the example of water flowing through different sections of a pipe?

In the example, water flows through sections of a pipe with different cross-sectional areas. According to the continuity principle, the flow rate (Q) remains the same at all sections. As the area decreases, the velocity increases, which can be mathematically represented as A1 * v1 = A2 * v2.

How is the speed of water affected by the pipe's cross-sectional area?

In areas of the pipe with smaller cross-sectional areas, the water speed increases. This is due to the continuity equation, which requires the flow rate to stay constant. If the area is smaller, the velocity must increase to keep the flow rate the same.

Why does water flow faster through a narrow pipe or nozzle?

Water flows faster through a narrow pipe or nozzle because the cross-sectional area is smaller. According to the continuity principle, if the area decreases, the velocity must increase to maintain the same flow rate. This is why water speeds up when you squeeze the nozzle of a hose.