Perbandingan Trigonometri Sudut-Sudut Istimewa
Summary
TLDRThis video tutorial introduces the concept of trigonometric ratios and special angles. It explains how certain angles, such as 30°, 45°, 60°, and 90°, have easily recognizable trigonometric values that do not require a calculator. The video walks through several examples, demonstrating how to calculate sine, cosine, and tangent for various angles using right triangles. Practical applications are shown, including finding the height of a tree or a tower using trigonometric ratios. The video aims to make trigonometry accessible and practical for everyday situations, with clear explanations and step-by-step solutions.
Takeaways
- 😀 Special angles in trigonometry are angles where the trigonometric ratios can be directly determined without a calculator.
- 😀 The special angles include 30°, 45°, 60°, and 90° in the first quadrant, and similar angles are present in the second, third, and fourth quadrants.
- 😀 It is essential to remember the values of trigonometric ratios for these special angles as they will be used throughout trigonometry lessons.
- 😀 For example, the value of cos 60° is 1/2, and the value of sin 45° is 1/2√2.
- 😀 Trigonometric ratios can be used to solve right triangle problems. For instance, if sin a = 0.5, the other trigonometric ratios can be derived.
- 😀 In solving for the sides of a right triangle, the Pythagorean theorem can be helpful to find missing side lengths.
- 😀 For a right triangle where sin a = 0.5, you can determine cos a and tan a by understanding their relationships to the sides of the triangle.
- 😀 In practical examples, trigonometric formulas such as sin, cos, and tan can be used to find unknown distances, such as the height of a tree or a tower.
- 😀 When solving for distances, it's crucial to visualize the problem and use the appropriate trigonometric function based on the known values (e.g., sin, cos, or tan).
- 😀 In word problems involving height and distance, angles of elevation or depression are often used with trigonometric functions to determine the unknown distances.
Q & A
What are special angles in trigonometry, and how are they used in real life?
-Special angles in trigonometry are angles for which the values of the trigonometric ratios (sine, cosine, tangent) can be directly determined without a calculator. These angles are often used in practical applications such as measuring heights, distances, or angles in fields like architecture, navigation, and engineering.
Which angles are considered special angles in trigonometry?
-The special angles in trigonometry are 30°, 45°, 60°, and 90°, which are commonly used in trigonometric calculations due to their simple and predictable ratio values.
How can you find the value of cos(60°) without a calculator?
-To find the value of cos(60°), we use the known trigonometric ratio for this special angle, which is 1/2.
What is the method to calculate the trigonometric ratios like sine, cosine, and tangent for any given angle?
-To calculate the trigonometric ratios for a given angle, we use a right triangle where the sine is the ratio of the opposite side to the hypotenuse, cosine is the ratio of the adjacent side to the hypotenuse, and tangent is the ratio of the opposite side to the adjacent side.
How do we solve a problem where sin(a) = 0.5 in a right triangle?
-When sin(a) = 0.5, we first express this as a ratio of the opposite side to the hypotenuse. Then, using the Pythagorean theorem, we can find the other sides of the triangle and calculate the corresponding trigonometric ratios such as cosine and tangent.
What is the process to solve for missing sides in a right triangle when given one trigonometric ratio?
-To solve for missing sides in a right triangle, we use the appropriate trigonometric ratio (sine, cosine, or tangent) based on the known information. Then, apply the Pythagorean theorem if needed to find the other side.
How do you calculate the height of an object, like a tree, when given the distance from the object and the angle of elevation?
-To calculate the height of an object, you use the tangent function, where the tangent of the angle of elevation is the ratio of the height of the object to the distance from the observer. You multiply the distance by the tangent of the angle to find the height.
In the given example, how did we find the height of a tree with a 60° angle of elevation from 60 meters away?
-To find the height of the tree, we used the tangent function. We multiplied the distance (60 meters) by the tangent of 60°, which gave the height as 60√3 meters.
What steps are involved in calculating the height of a tower when the distance and angle of elevation are given?
-To calculate the height of a tower, you use the tangent function. First, find the tangent of the given angle of elevation. Then, multiply this by the distance from the tower to the observer. Add any additional height, such as the observer's eye level, if necessary.
How do we calculate the height of a tower when the angle of elevation is 30° and the distance is 150 meters?
-In this case, we used the tangent function where tan(30°) = height of the tower / 150 meters. After calculating, we added the height of the observer's eyes to get the total height of the tower.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

(TRIK) Perbandingan Trigonometri Sudut Berelasi #fazanugas

Video Pembelajaran Matematika Materi Trigonometri Kelas 10 - Nilai Trigonometri pada Sudut Istimewa

Trigonometric Ratios (Tagalog Math)
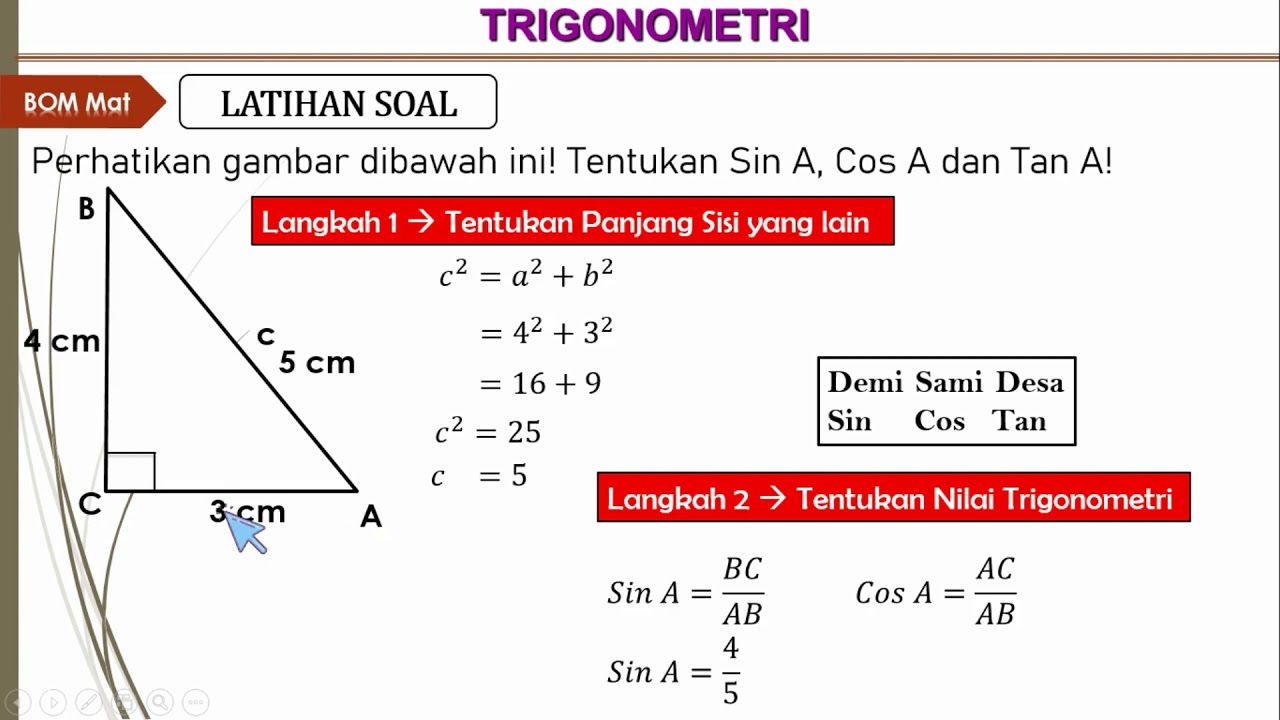
Perbandingan trigonometri pada segitiga siku siku, Menjelaskan rasio trigonometri

TRIGONOMETRI - Ukuran Sudut dan Perbandingan Trigonometri

Matematika SMA - Trigonometri (1) - Pengenalan Trigonometri, Perbandingan Trigonometri (A)
5.0 / 5 (0 votes)