Introducción a la racionalización
Summary
TLDREn este video se explica el proceso de racionalización de radicales, el cual consiste en eliminar las raíces del denominador de una expresión matemática para simplificarla. Se abordan diversos tipos de expresiones con radicales, desde denominadores con un solo término hasta aquellos con dos o tres términos, y se proporcionan ejemplos prácticos para entender cómo proceder en cada caso. Además, se invita a los estudiantes a practicar con ejercicios específicos para identificar la cantidad de términos en el denominador y mejorar su comprensión del tema.
Takeaways
- 😀 La racionalización de radicales consiste en eliminar las raíces del denominador de una fracción para simplificar las operaciones.
- 😀 Para eliminar un radical, el exponente dentro de la raíz debe ser igual al índice de la raíz, como en el caso de raíz cuadrada de 3 al cuadrado.
- 😀 Cuando el exponente y el índice de la raíz coinciden, el radical puede eliminarse fácilmente, como en el ejemplo de raíz quinta de 3 a la 5.
- 😀 Existen diferentes tipos de expresiones que se pueden racionalizar, dependiendo de cuántos términos haya en el denominador.
- 😀 Las expresiones más comunes que se racionalizan son aquellas con un solo término en el denominador, ya sea con raíz cuadrada o de otro tipo (como cúbica, cuarta, etc.).
- 😀 Otra forma común de racionalizar es cuando el denominador tiene dos términos, ya sea con una raíz o ambos con raíces.
- 😀 También es posible encontrar denominadores con tres términos, que pueden contener raíces en algunos o todos sus términos.
- 😀 En la racionalización, la atención principal está en el denominador, aunque a veces también se debe considerar el numerador, especialmente en temas como límites.
- 😀 Es importante diferenciar entre casos con un solo término, dos términos o tres términos en el denominador al racionalizar.
- 😀 El ejercicio propuesto permite practicar identificando cuántos términos tiene el denominador en diversas expresiones con radicales, ayudando a entender mejor el proceso de racionalización.
Q & A
¿Qué significa racionalizar en el contexto de la matemática?
-Racionalizar consiste en eliminar los radicales (raíces) del denominador de una fracción o expresión algebraica para simplificar las operaciones. Esto hace que las operaciones sean más sencillas.
¿Cómo se eliminan los radicales en una expresión matemática?
-Se eliminan los radicales cuando el exponente dentro de la raíz es igual al índice de la raíz. Por ejemplo, si tienes una raíz cuadrada de un número elevado al cuadrado, puedes eliminar la raíz.
¿Qué es lo más sencillo que se puede hacer para eliminar un radical?
-Lo más sencillo es que el exponente de lo que está dentro de la raíz sea igual al índice de la raíz. En ese caso, la raíz se elimina directamente.
¿Qué tipo de expresiones se deben racionalizar?
-Las expresiones más comunes que se racionalizan incluyen aquellas en las que el denominador tiene un solo término con raíz, varios términos con raíces, o incluso términos con raíces de índices distintos como cúbicas, cuarta o quinta.
¿Cuál es la diferencia entre racionalizar una fracción con un denominador de un solo término y uno de dos o tres términos?
-En un denominador de un solo término, se tiene una expresión con raíz. En un denominador de dos o tres términos, los radicales pueden estar presentes en uno o más términos, y se deben aplicar diferentes métodos para racionalizar dependiendo de la cantidad de términos y el tipo de raíces involucradas.
¿Qué sucede cuando hay dos términos en el denominador y uno de ellos tiene una raíz?
-Cuando hay dos términos en el denominador, puede ser que uno tenga raíz y el otro no, o ambos pueden tener raíces. En este caso, la racionalización se realiza mediante una técnica adecuada para tratar con dos términos en el denominador.
¿Cómo se manejan expresiones en las que hay tres términos en el denominador?
-En el caso de tres términos en el denominador, se puede tener una raíz en uno, dos, o los tres términos. La racionalización de estos casos es más compleja y requiere un enfoque específico para cada situación.
¿Por qué es importante diferenciar cuándo hay uno, dos o tres términos en el denominador al racionalizar?
-Es fundamental diferenciar la cantidad de términos en el denominador porque cada caso requiere un enfoque distinto para realizar la racionalización correctamente. Ignorar esta diferencia podría llevar a errores en el proceso.
En el caso de expresiones con radicales en el denominador, ¿qué debemos hacer primero?
-Primero, debemos observar cuántos términos tiene el denominador y si esos términos contienen raíces. Esto nos ayudará a aplicar la técnica adecuada para racionalizar la expresión.
¿Por qué el numerador generalmente no se considera al racionalizar?
-En la mayoría de los casos, se pone el foco en el denominador, ya que es allí donde se encuentran los radicales que deben eliminarse. Aunque a veces se debe racionalizar también el numerador, esto suele ocurrir en casos especiales como en los límites.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Racionalización de Denominadores 1ra Parte

SIMPLIFICAR Y RACIONALIZAR UNA EXPRESIÓN ALGEBRAICA

Racionalización de denominadores (CASO 2)
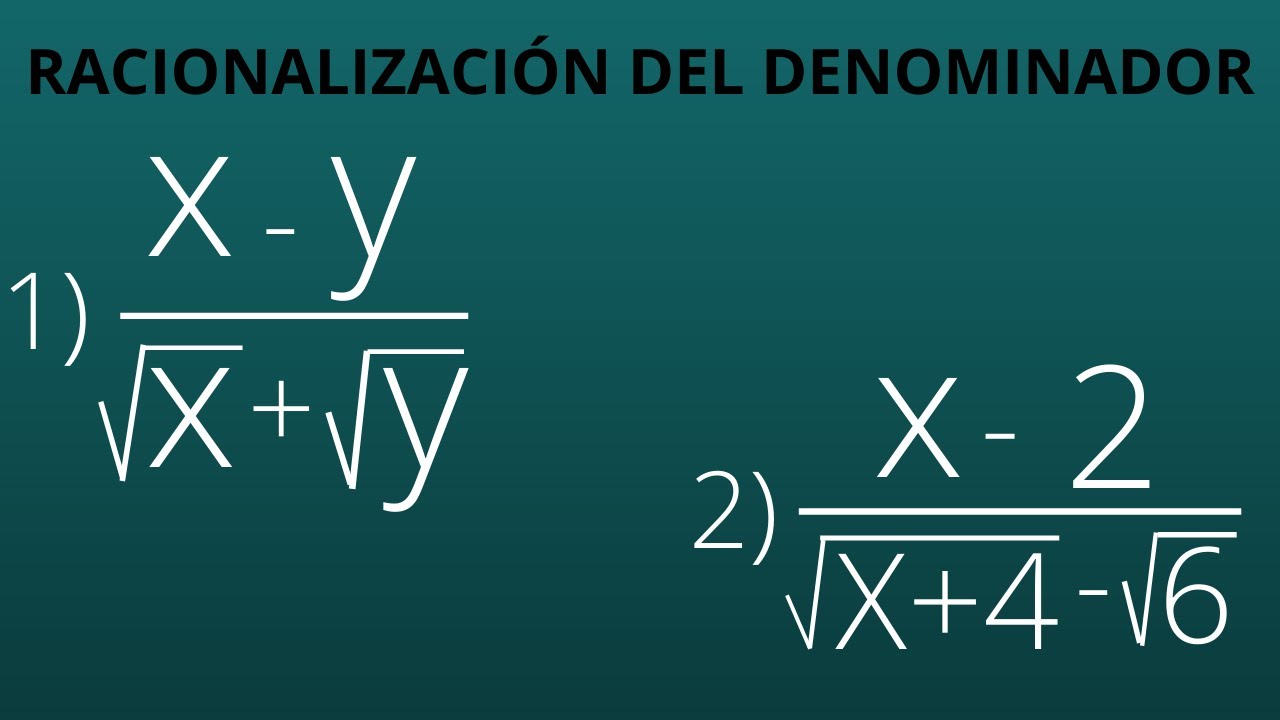
Racionalización del denominador (binomio) con expresiones algebraicas, explicado paso a paso.

Solución de límites por racionalización | Ejemplo 2

SIMPLIFICACIÓN DE EXPRESIONES CON RADICALES EJEMPLO 3 (EJEMPLOS RESUELTOS)
5.0 / 5 (0 votes)
