KESEBANGUNAN (Materi Kelas 9 SMP)

Summary

In this video, the host explains the concept of similarity in geometry, particularly focusing on the properties of similar figures. He begins by discussing the visual analogy of resizing images and how their shapes remain unchanged while their sizes vary. The video then covers the rules for determining if two shapes are similar, such as comparing corresponding angles and sides. The host also goes into specific examples, such as trapezoids and triangles, and guides viewers through problem-solving techniques, highlighting key mathematical principles of similarity in two-dimensional figures.

Takeaways

• 😀 The video explains the concept of similarity in geometry, focusing on how shapes can remain proportionally the same but change in size.
• 😀 Congruence and similarity are foundational topics in mathematics for 9th-grade students, with this video building on a previous discussion about congruence.
• 😀 Similarity is explained through the concept of resizing shapes without altering their internal proportions, such as scaling images or figures in PowerPoint.
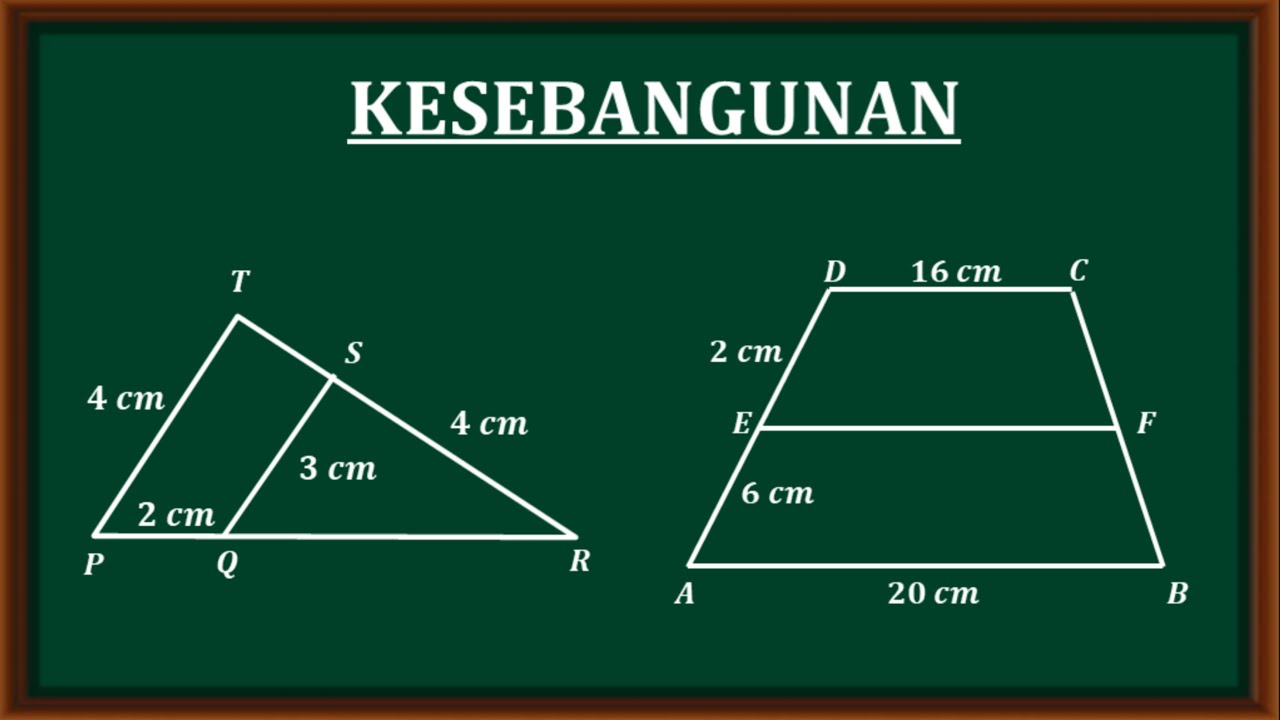
• 😀 The video provides visual examples using trapezoids and rectangles to illustrate when shapes are considered similar based on their corresponding angles and proportional side lengths.
• 😀 For shapes to be considered similar, their corresponding angles must be equal, and their corresponding sides must have the same ratio.
• 😀 The video explains the process of checking similarity in polygons, emphasizing the importance of comparing corresponding sides and angles to determine similarity.
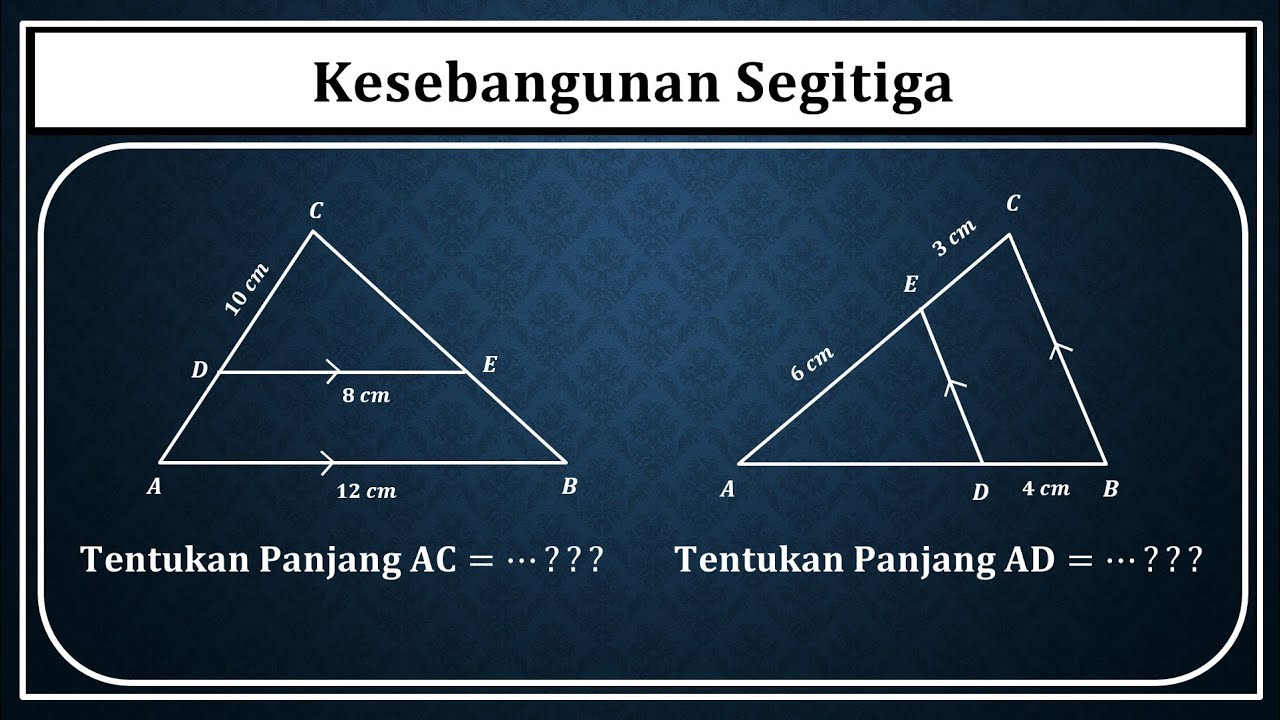
• 😀 Special consideration is given to triangles, where similarity can be established by either equal corresponding angles or proportional corresponding sides.
• 😀 In triangles, it is sufficient for only one condition (either equal angles or proportional sides) to determine similarity, unlike other polygons where both conditions must be satisfied.
• 😀 The video includes a variety of mathematical examples, such as comparing side lengths of similar trapezoids and rectangles to determine their proportionality.
• 😀 It also provides step-by-step problem-solving methods for finding unknown side lengths in similar figures, using cross-multiplication and simplification techniques.

Q & A

What is the main topic of this video?

The main topic of the video is about the concept of similarity in geometry, specifically focusing on similar figures and their properties.

What is the definition of 'similarity' in geometry, as explained in the video?

Similarity in geometry refers to two shapes that have the same shape but different sizes. The figures are proportional, meaning their corresponding angles are equal, and the corresponding sides have equal ratios.

How does the video explain the concept of similarity using an image manipulation example?

The video explains similarity by showing how an image can be resized. When a picture is resized from the corner, the shape remains unchanged, which is an example of similar figures where the size changes but the proportions stay the same.

What are the two conditions for two polygons to be considered similar?

The two conditions for similarity are: (1) the corresponding angles must be equal, and (2) the corresponding sides must be proportional, meaning the ratio of corresponding sides is the same.

Why is the second trapezium example not considered similar to the first?

The second trapezium is not similar because the ratio of the corresponding sides is not equal. For the figures to be similar, the ratio of the corresponding sides must be the same.

What is the difference between similarity in general polygons and triangles?

In general polygons (like quadrilaterals), both conditions (equal angles and proportional sides) must be satisfied for similarity. However, for triangles, only one condition must be satisfied: either the corresponding angles must be equal or the corresponding sides must have the same ratio.

In the case of triangles, what does the video mean by 'OR' for the conditions of similarity?

For triangles, the condition of similarity is considered satisfied if either the corresponding angles are equal or the corresponding sides are proportional. Unlike other polygons, for triangles, it's enough for just one condition to be met.

What method does the video suggest for comparing sides of similar figures?

The video suggests comparing the corresponding sides of the figures by simplifying the ratios. For example, if the sides are not equal, you can simplify them to check if the ratios are the same.

What is the importance of using corresponding sides when comparing similar figures?

Using corresponding sides is essential because only these sides maintain the proportional relationship in similar figures. Comparing sides that do not correspond can lead to incorrect conclusions about the similarity of the figures.

Can two triangles be considered similar if their corresponding angles are not equal?

No, two triangles cannot be considered similar if their corresponding angles are not equal. One of the key conditions for similarity in triangles is that all corresponding angles must be equal.