math animations derivatives
Summary
TLDRThis script explores the concept of slope as a measure of steepness, defined as the ratio of elevation change to horizontal distance. It illustrates how a larger slope indicates a steeper incline and discusses the use of tangent lines to determine the slope at specific points. The script then delves into calculus, explaining derivatives as the mathematical embodiment of slope, with practical applications such as calculating velocity and acceleration in motion. It highlights the sum and product rules for finding derivatives, emphasizing the importance of understanding calculus in various fields.
Takeaways
- 📏 The steepness of an incline is defined as the ratio of the change in elevation to the change in horizontal distance, known as the slope.
- 🌄 A hill with a higher slope value is steeper than one with a lower slope value.
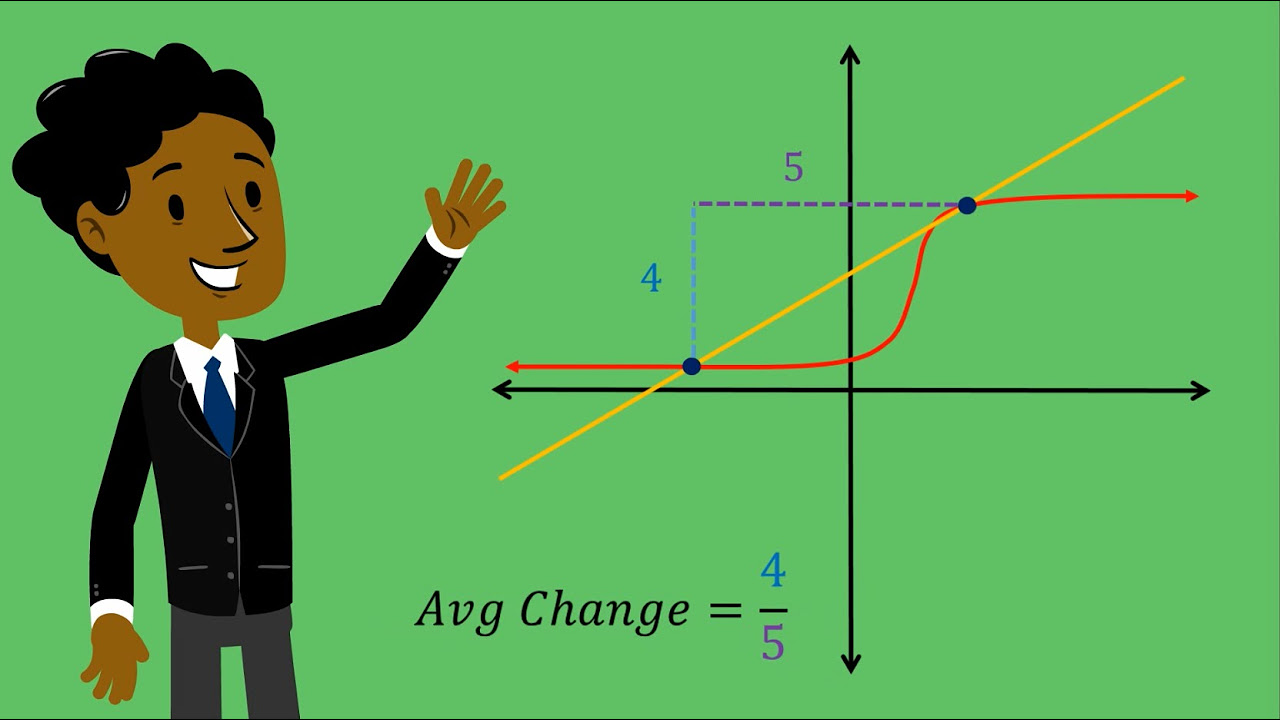
- 📈 The slope of a hill can be determined by connecting two points on the hill with a straight line, called a chord, and calculating its slope.
- 🤔 As the second point on the hill gets closer to the first, the slope of the chord approaches the slope of the hill at that point.
- 🔍 The slope at a specific point on a hill is represented by the slope of the tangent line at that point, which is the limit of the chord's slope as the points converge.
- 📐 The concept of 'delta' (Δ) is introduced to represent small changes in variables, such as Δy for a small change in y and Δx for a small change in x.
- 🧮 The ratio of Δy to Δx is a representation of the slope, and as these small changes approach zero, the ratio becomes the derivative, denoted as dy/dx.
- 🔄 The derivative of a function at any point is the slope of the tangent to the function's graph at that point.
- 📚 The derivative of a linear function is constant, reflecting the constant slope of the line.
- ✅ Derivatives can be calculated for various functions, including trigonometric functions like sine and cosine, using rules such as the sum rule and the product rule.
- 🚀 Derivatives have practical applications in physics, such as calculating velocity and acceleration from displacement in the motion of a rocket.
Q & A
What is the definition of steepness on an incline?
-Steepness is defined as the ratio of the change in elevation to the change in horizontal distance.
What is the term used to describe the steepness ratio?
-The term used to describe the steepness ratio is 'slope'.
How is the slope of an incline calculated?
-The slope is calculated by dividing the elevation increase by the horizontal distance over which it occurs.
What does a slope of 3 indicate about a hill compared to a slope of 0.15?
-A slope of 3 indicates that a hill is twice as steep as one with a slope of 0.15.
How does the slope relate to the steepness of a hill?
-A larger slope indicates a steeper hill, while a slope near zero suggests an easy incline.
What is the term for a straight line connecting two points on a hill?
-A straight line connecting two points on a hill is called a 'chord'.
What is the significance of the tangent line in relation to the slope of a hill?
-The tangent line represents the slope of the hill at a particular point and is the limit of the chord as the second point approaches the first.
What is the mathematical symbol used to denote the derivative of a function?
-The derivative of a function is denoted by the symbol 'dy/dx', which represents the derivative with respect to x of the quantity y.
How does the derivative relate to the slope of a function?
-The derivative of a function at any given point is the slope of the tangent line to the function at that point.
What is the sum rule in the context of derivatives?
-The sum rule states that the derivative of a sum is the sum of the derivatives of the individual functions.
Can you provide an example of using the product rule to find a derivative?
-The product rule is used to find the derivative of a product of two functions, y * z, which is calculated as y * the derivative of z + z * the derivative of y.
What is the application of derivatives in the context of a rocket's motion?
-In the context of a rocket's motion, the derivative of displacement (s) with respect to time (t) gives the velocity, and the second derivative gives the acceleration.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Introduction to Slope

Kemiringan (Gradien) Hal 220-230 Bab 5 Persamaan Garis Lurus Kelas 8 Kurikulum Merdeka Belajar

The paradox of the derivative | Chapter 2, Essence of calculus

What is average rate of change?
Calculus - Average Rate of Change of a Function

Derivative as a concept | Derivatives introduction | AP Calculus AB | Khan Academy
5.0 / 5 (0 votes)