Pengenalan Sistem Kontrol PID Bagian 1

Summary

This video explains the fundamentals of PID (Proportional, Integral, Derivative) control systems, focusing on their application in regulating temperature and other systems. It covers the historical development of PID controllers, their mathematical foundations, and real-world applications. The speaker demonstrates the differences between a system with and without PID control, highlighting the benefits of stability and responsiveness while showing examples of system behaviors. The video also delves into the challenges of balancing speed and accuracy in control systems, offering valuable insights for understanding and applying PID control techniques.

Takeaways

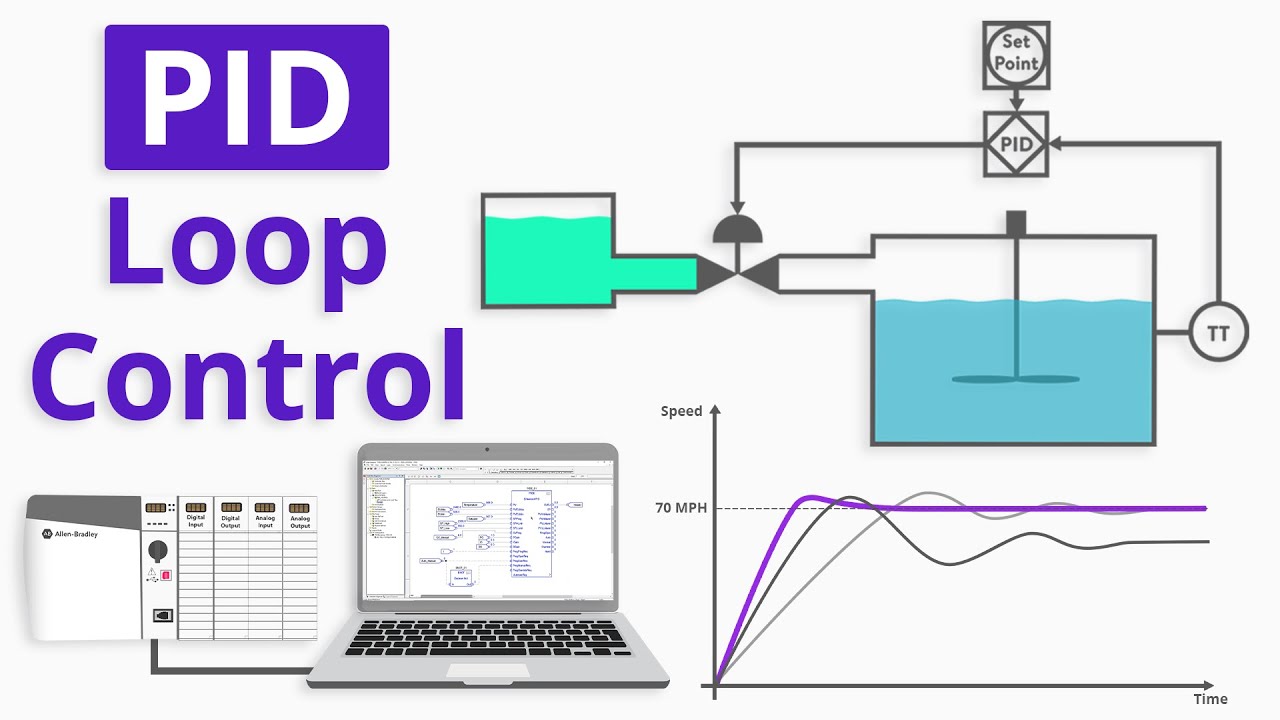
• 😀 The video discusses the Proportional-Integral-Derivative (PID) control system, which is an application of calculus in control systems.
• 😀 PID control was first introduced in the 1700s for ship steering and was further developed in the 1920s, continuing to be used in modern automation and industrial machinery.
• 😀 The primary function of PID is to stabilize a system by minimizing error using feedback from the system’s output.
• 😀 PID not only uses current feedback but also predicts future system states based on past data.
• 😀 A PID control system consists of three parts: Proportional (P), Integral (I), and Derivative (D).
• 😀 The Proportional component is calculated by multiplying the error (the difference between the setpoint and the current output) by a proportional constant.
• 😀 PID systems aim to reduce oscillations and improve stability by adjusting system outputs based on errors.
• 😀 A simple system without PID control may have high oscillations, whereas with PID, the system becomes smoother and more stable in response to disturbances.
• 😀 The video also demonstrates a case study where a heating system's temperature is controlled, showing how PID reduces fluctuations compared to simpler control methods.
• 😀 The Proportional-only method is slower and cannot completely eliminate error, as the system doesn't adjust to exact setpoints, unlike the more advanced PID method which can improve system stability over time.

Q & A

What is the main topic discussed in the video?

The video discusses the Proportional-Integral-Derivative (PID) control system, which is used in automation, particularly in systems like ship steering and industrial machines.

When was the PID control system first introduced?

The PID control system was first introduced in the 1700s, and it was initially applied to ship steering systems. It has since evolved and is widely used in various automation systems today.

What are the main components of the PID control system?

The PID control system consists of three main components: Proportional (P), Integral (I), and Derivative (D), each playing a specific role in managing system errors.

How does the PID control system work?

The PID control system works by constantly comparing the system's output to a desired setpoint, then adjusting the system's input to minimize the error between them.

What is the purpose of the feedback loop in the PID system?

The feedback loop in the PID system helps ensure that the output of the system is continuously monitored and corrected to match the setpoint, maintaining stability and accuracy.

Can you explain how the Proportional component (P) works in the PID system?

The Proportional component calculates the error by comparing the current value to the desired setpoint and adjusts the output in proportion to this error. Larger errors result in larger adjustments.

What happens if only the Proportional component is used in the control system?

If only the Proportional component is used, the system may stabilize, but it will likely experience oscillations and will not fully reach the desired setpoint. It may leave residual errors.

How does the Integral component (I) improve the PID control system?

The Integral component addresses accumulated errors over time, helping to eliminate residual steady-state errors that the Proportional component alone cannot correct.

What role does the Derivative component (D) play in the PID system?

The Derivative component predicts future errors based on the rate of change, allowing the system to react more quickly to disturbances and smooth out sudden changes.

Why is it important to model the system using transfer functions in PID control?

Modeling the system with transfer functions is important because it allows the behavior of the system to be represented mathematically, enabling accurate simulations and tuning of the PID controller using software.