Geometría Analítica: Ecuación de la elipse dados foco y la excentricidad.
Summary
TLDREn este video, se resuelve un problema relacionado con la ecuación de una elipse, utilizando la excentricidad y los focos. El objetivo es determinar la ecuación y los elementos clave de la elipse, como el centro, los vértices y los extremos. A través de la observación de los focos y la excentricidad, se identifican los valores necesarios para la ecuación, que luego se representa gráficamente. Además, se exploran las fórmulas y relaciones matemáticas, proporcionando un enfoque paso a paso para comprender cómo resolver este tipo de problemas de geometría analítica.
Takeaways
- 😀 Se está resolviendo un problema de elipse con excentricidad de dos tercios y un centro en el origen (0, 0).
- 😀 El primer foco de la elipse está ubicado en -20, lo que indica que la elipse es horizontal.
- 😀 Se requiere conocer el valor de 'h' para determinar la ecuación completa de la elipse.
- 😀 La excentricidad y la distancia entre los focos proporcionan información clave para resolver el problema.
- 😀 El valor de la excentricidad está dado por 2, lo que ayuda a identificar la relación entre los ejes de la elipse.
- 😀 Los focos se encuentran sobre el eje X, lo que permite determinar la orientación horizontal de la elipse.
- 😀 La fórmula general para la elipse se puede deducir a partir de los datos conocidos, como los focos y la excentricidad.
- 😀 El centro de la elipse se determina como (0, 0) observando la ubicación de los focos en el eje X.
- 😀 La ecuación de la elipse resultante tiene la forma: x²/55 + y²/25 = 1.
- 😀 Para graficar la elipse, se necesita encontrar los vértices y los extremos de la elipse, que se calculan a partir de los valores 'a' y 'b'.
- 😀 Los vértices de la elipse son los puntos (±3, 0) y los extremos son los puntos (0, ±2.23).
Q & A
¿Cómo podemos determinar si la elipse es horizontal o vertical?
-Podemos determinar la orientación de la elipse observando la ubicación de los focos. Si los focos están a lo largo del eje x, la elipse es horizontal; si están a lo largo del eje y, la elipse es vertical.
¿Qué nos indica la excentricidad de una elipse?
-La excentricidad de una elipse mide cuán 'alargada' es la figura. En este caso, la excentricidad de 2/3 sugiere que la elipse tiene una forma alargada, pero no excesivamente.
¿Cuál es la importancia de conocer el centro de la elipse?
-El centro de la elipse es crucial para escribir su ecuación. En este caso, dado que los focos están ubicados en el eje x, podemos concluir que el centro está en el origen (0, 0).
¿Cómo se determina la ecuación de la elipse?
-La ecuación de la elipse se determina a partir de los valores de los semiejes mayor (a) y menor (b), la excentricidad y la ubicación de los focos. En este caso, la ecuación es de la forma (x^2 / a^2) + (y^2 / b^2) = 1.
¿Qué representa la distancia entre el centro y los focos?
-La distancia entre el centro y los focos se relaciona con la excentricidad y se utiliza para calcular los valores de los semiejes mayor y menor de la elipse.
¿Cómo podemos encontrar los vértices de la elipse?
-Los vértices de la elipse están a una distancia de 'a' unidades del centro a lo largo del eje mayor. En este caso, los vértices son (-3, 0) y (3, 0).
¿Qué son los extremos de la elipse y cómo se calculan?
-Los extremos son puntos en los que la elipse se cruza con el eje menor. Se calculan a partir del valor de 'b', y en este caso, son los puntos (0, -2.3) y (0, 2.3).
¿Por qué es importante calcular la distancia focal?
-La distancia focal es importante para entender la forma y las características de la elipse, como la excentricidad, que afecta cómo se distribuyen los puntos de la elipse con respecto a los focos.
¿Cómo se determina el valor de 'a' y 'b' en la ecuación de la elipse?
-El valor de 'a' se determina a partir de la distancia entre los vértices, mientras que 'b' se calcula a partir de la relación entre la excentricidad y el valor de 'a'.
¿Qué es el directriz y cómo se relaciona con la elipse?
-La directriz es una línea a una distancia 'd' del centro de la elipse, y se utiliza en la definición geométrica de la elipse. La distancia entre cualquier punto de la elipse y un foco es siempre menor que la distancia entre el punto y la directriz.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
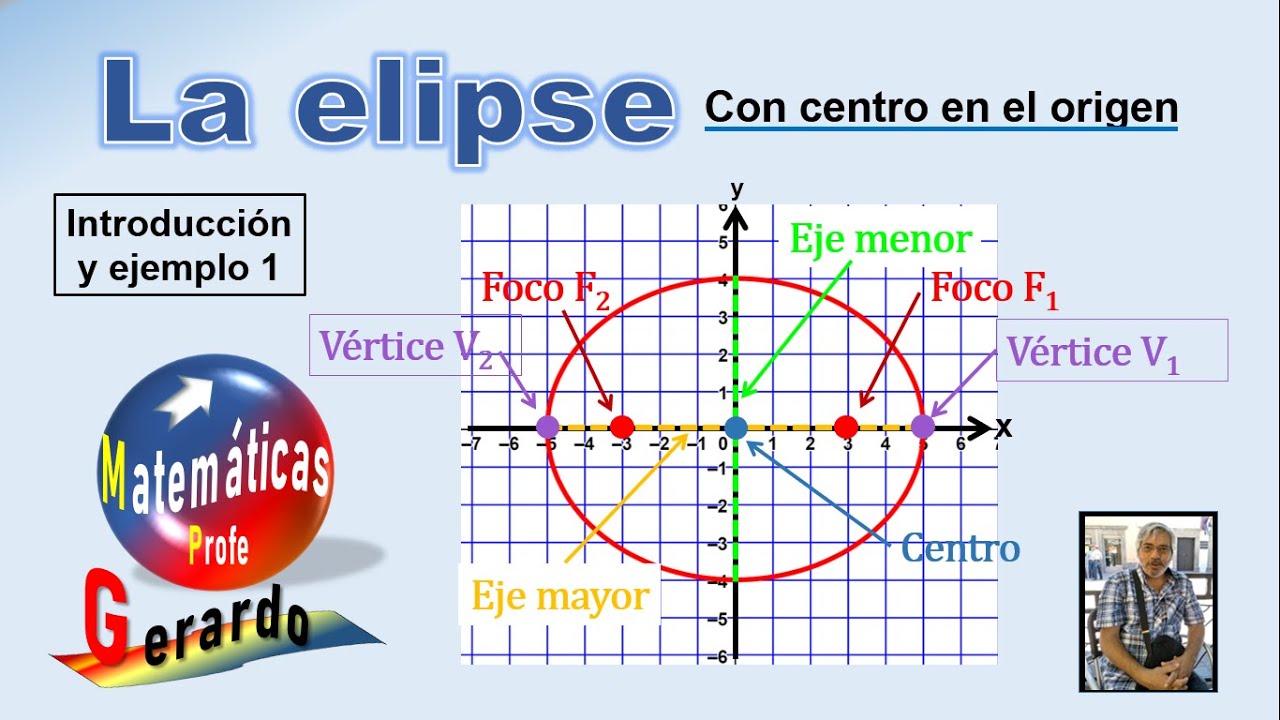
La elipse con centro en el origen. Introducción y ejemplo 1.

HALLAR LA EXCENTRICIDAD Y LA ECUACIÓN DE UNA ELIPSE

63. Encontrar a todos los elementos de una elipse cuando te dan su ecuación general.

Gráfica y elementos de la Elipse conociendo la ecuación canónica | Ejemplo 1

✅ELIPSE con centro FUERA del ORIGEN [100% 𝙀𝙛𝙚𝙘𝙩𝙞𝙫𝙤 😎🫵💯] Geometría Analítica

Geometría Analítica: Circunferencia y dos punto detecta un error de cálculo.
5.0 / 5 (0 votes)
