METODE NUMERIK P6 PART 2/2 | METODE ITERASI TITIK TETAP UNTUK MENYELESAIKAN PERSAMAAN NON LINIER

Summary

In this lecture, Fitri Azzahra Kumala discusses the sixth session of the numerical methods course, focusing on the nonlinear equation solutions using the fixed-point iteration method. She explains how this open method does not require a bracketing interval like closed methods do, and outlines its iterative process. The lecture also demonstrates solving an equation (x^2 - 2x - 3 = 0) using this method in Microsoft Excel, detailing the procedure for each iteration and its convergence. She emphasizes that the method can either converge or diverge, depending on the iteration procedure.

The video is abnormal, and we are working hard to fix it.
Please replace the link and try again.

Q & A

What is the focus of this lecture?

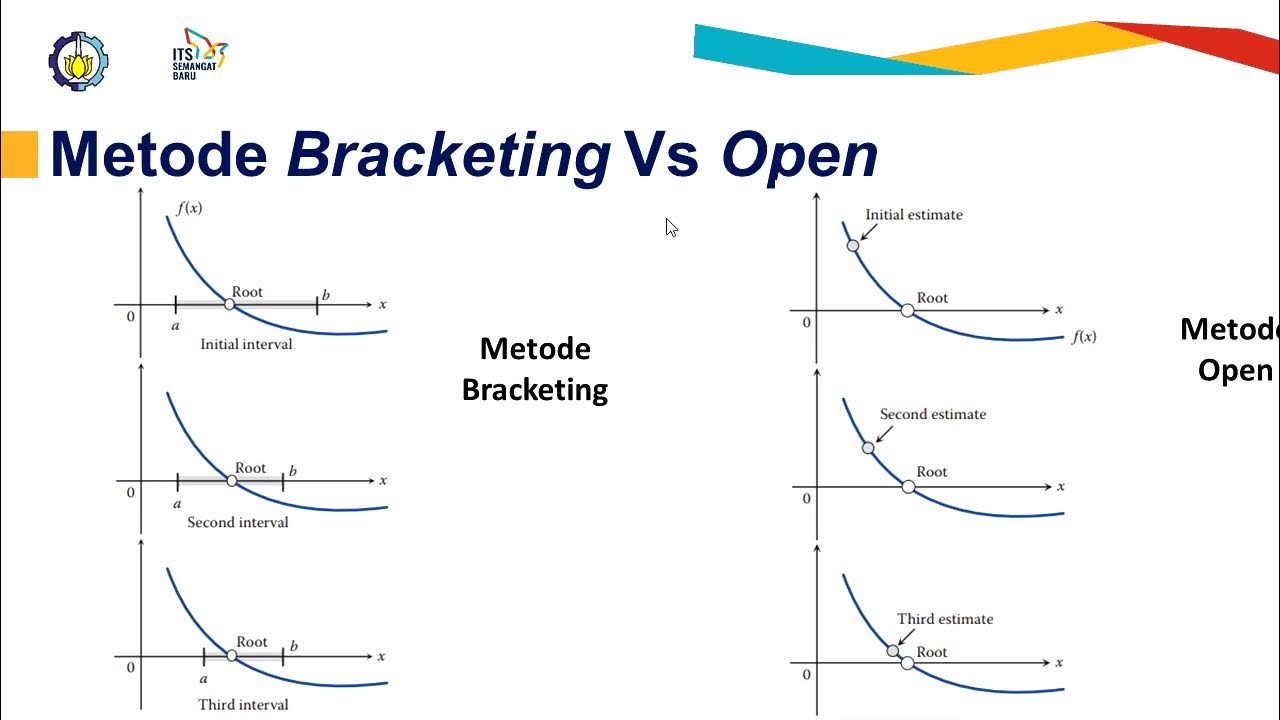
This lecture focuses on solving nonlinear equations using numerical methods, specifically the Fixed Point Iteration method, which is a type of open method that does not require an enclosing interval.

What is the main difference between open and closed methods in numerical solutions?

The main difference is that open methods, like the Fixed Point Iteration, do not require an interval that bounds the root, while closed methods, like the bisection method, require such an interval.

How does the Fixed Point Iteration method work?

In Fixed Point Iteration, an equation of the form F(X) = 0 is rewritten as X = G(X). Starting with an initial guess, the method iteratively updates the guess using the relation X_{r+1} = G(X_r), and the process continues until convergence is achieved.

What does the convergence of the Fixed Point Iteration method depend on?

The convergence depends on the choice of the function G(X) and the initial guess. If the method converges, it will do so rapidly, but it may also diverge if the conditions are not suitable.

What is the stopping criterion for the Fixed Point Iteration method?

The iteration stops when the absolute difference between successive guesses, |X_{r+1} - X_r|, becomes smaller than a predefined tolerance (epsilon) or when the relative change |X_{r+1} - X_r| / |X_{r+1}| becomes smaller than another predefined threshold (delta).

Can you explain the example used to demonstrate the Fixed Point Iteration?

The example used is solving the equation x² - 2x - 3 = 0. The equation is manipulated to create different forms of G(X) for iteration, such as X = sqrt(2X + 3), X = 3/(X - 2), and X = (X² - 3)/2. These forms are used to perform iterations starting with an initial guess of 4.

What happens when the method does not converge monotonically?

If the iteration does not converge monotonically, it may oscillate. In the example, one of the procedures results in oscillation and eventually converges to a root after many iterations, while others may diverge.

What is the significance of the epsilon value in the example?

Epsilon represents the tolerance for the stopping criterion. In the example, epsilon is set to 0.000001, and the iterations continue until the absolute difference between successive guesses is smaller than epsilon.

How can we determine if the method is diverging?

If the values of successive iterations grow larger or do not approach a specific value, the method is diverging. In the example, the third iteration method for solving the equation diverged, which indicated it was not suitable for this particular function.

What are the final results from the iteration procedures in the example?

From the first iteration procedure, the approximation for the root is 3. From the second procedure, the root is approximately -1, and from the third, the method diverged, meaning it didn't converge to a root.