PID Automatic Control - presentation

Summary

This presentation delves into the PID controller, a common feedback mechanism with proportional, integral, and derivative terms. It explains how these terms work together to minimize errors in system outputs, using a self-driving car as an example to illustrate the practical application of PID in correcting deviations, accumulating errors over time, and anticipating future errors. The challenge of determining the optimal coefficients for PID control is also highlighted, emphasizing the need for extensive experimentation and experience.

Takeaways

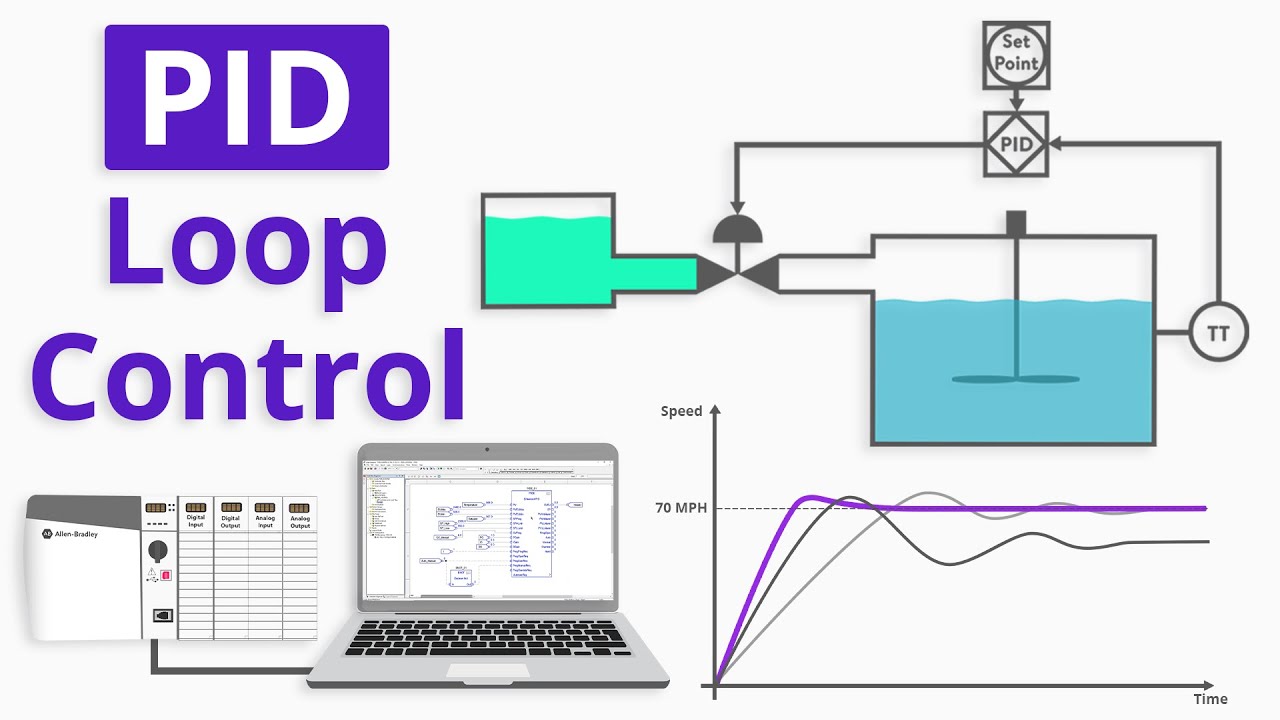
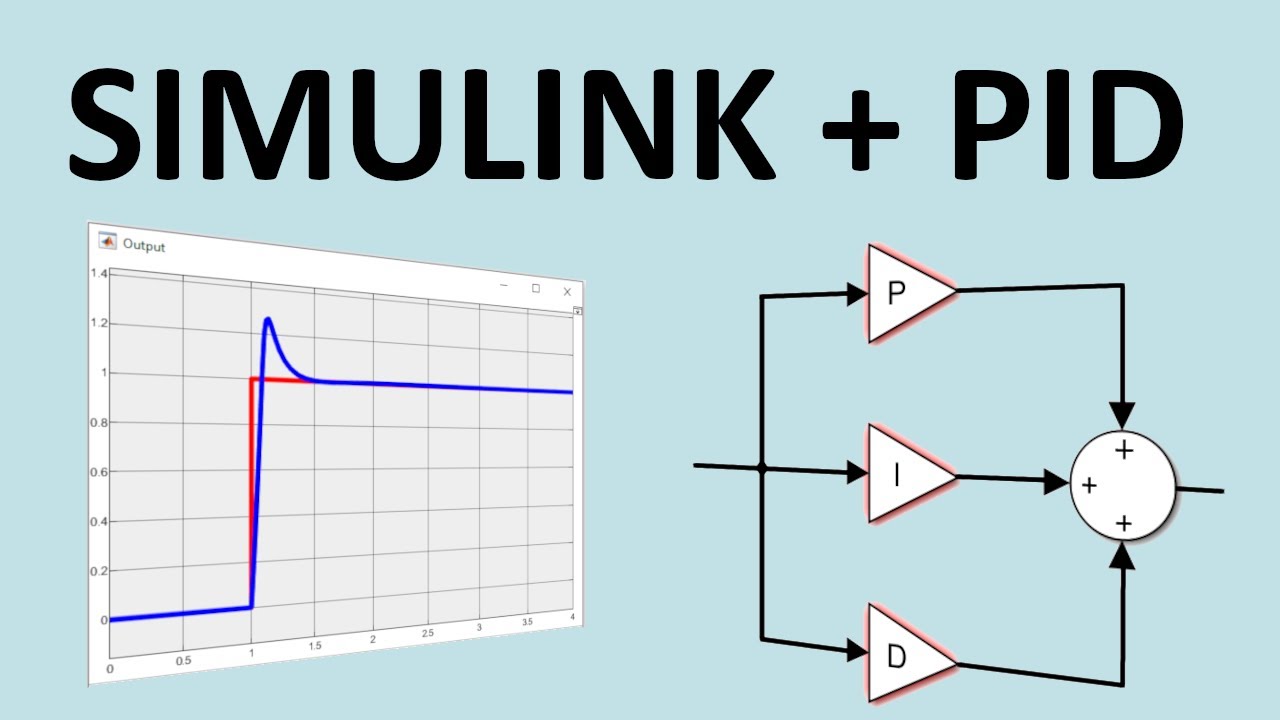
• 🔧 The PID controller is a feedback control system that includes Proportional (P), Integral (I), and Derivative (D) terms to adjust the system's output towards a reference value.
• 📉 The Proportional term in a PID controller responds to the current position error, aiming to drive it to zero by adjusting the control signal proportionally to the error.
• 🔄 The Integral term addresses the accumulated error over time, contributing to the control signal to reduce the average error between past outputs and reference values.
• 🚀 The Derivative term anticipates future errors by responding to the rate of change of the error, which helps in smoothing out rapid changes in the system's response.
• 📈 The formula for a PID controller combines the proportional gain (KP), integral gain (Ki), and derivative gain (KD) to calculate the control effort (UT).
• 📊 The transfer function of a PID controller can be derived using the Laplace transform, resulting in a formula that includes s², s, and 1/s terms, representing the derivative, proportional, and integral effects, respectively.
• 🚗 In self-driving cars, the PID controller uses sensor inputs to generate control signals that adjust the car's steering, throttle, and brakes to maintain the desired state.
• 🛠 The P component of a PID in self-driving cars corrects immediate deviations from the desired path, while the I component eliminates systematic errors over time.
• 🔎 The D component in self-driving cars evaluates the rate of error change to improve response time and smooth out steering or acceleration adjustments.
• 🔬 Determining the optimal coefficients for a PID controller often requires extensive experimentation and experience, ensuring the system performs efficiently and accurately.
• 👋 The presentation concludes by emphasizing the importance of continuous testing and adjustment of PID coefficients for achieving excellent control in various applications.

Q & A

What is a PID controller?

A PID controller is a common feedback controller that consists of proportional, integral, and derivative terms, used to control a process or system by adjusting the control signal based on the error between the desired setpoint and the actual output.

What does the proportional term in a PID controller do?

The proportional term in a PID controller contributes to the control signal proportionally to the current position error, aiming to drive the position error to zero and move the output towards the reference value.

How does the integral term of a PID controller work?

The integral term contributes to the control signal proportionally to the sum of all past errors, attempting to drive the total accumulated error to zero and thus correcting the average of all past output values towards the average of all past reference values.

What is the purpose of the derivative term in a PID controller?

The derivative term contributes to the control signal in proportion to the rate of change of the error, aiming to drive the derivative of the error to zero, which helps to make the output move at the same rate as the reference value, improving the system's response time.

What are the three gains in a PID controller and what do they represent?

The three gains in a PID controller are KP (proportional gain), Ki (integral gain), and KD (derivative gain). They represent the strength of the proportional, integral, and derivative terms respectively and determine the controller's response to the error.

Can you explain the formula for the proportional term in a PID controller?

The formula for the proportional term is UT = KP * e, where UT is the control effort, KP is the proportional gain, and e is the error.

How is the integral term of a PID controller represented mathematically?

The integral term is represented by the formula UT = Ki * ∫(from 0 to T) of e(t) dt, where UT is the control effort, Ki is the integral gain, and e(t) is the error at time t.

What is the mathematical representation of the derivative term in a PID controller?

The derivative term is represented by the formula UT = KD * (de/dt), where UT is the control effort, KD is the derivative gain, and de/dt is the derivative of the error with respect to time.

How does a PID controller adjust the behavior of a self-driving car?

A PID controller in a self-driving car adjusts the car's actuators such as steering, throttle, and brakes based on the error between the desired state (position, velocity) and the actual state obtained from sensors. The P component corrects immediate deviations, the I component eliminates steady-state errors, and the D component smooths out rapid changes in control.

What challenges are faced when determining the coefficients for a PID controller?

Determining the coefficients for a PID controller requires a lot of experimentation and experience. It involves continuous testing to select the appropriate values of KP, Ki, and KD that will achieve optimal control performance.

How can the transfer function of a PID controller be derived using the Laplace transform?

The transfer function of a PID controller can be derived by applying the Laplace transform to the time-domain equation of the controller. The result is a function G(s) = (KD * s² + KP * s + Ki) / (s + a constant), where s is the Laplace operator and the constant arises from the definite integral term.