#MECFLU 20 Equação da Quantidade de Movimento P01 - Mecânica dos Fluidos

Summary

In this lesson on Fluid Mechanics, Michele Camargo explains the development of the momentum equation for a steady-state system. She reviews key principles, such as Newton’s second law and the relationship between mass, acceleration, and force. The lecture covers concepts like velocity variation, momentum, and the forces involved when fluid moves through pipes, especially in changing directions. Additionally, she explores the importance of pipe fittings and fluid forces in real-world applications. The session concludes with suggestions for further reading and invites feedback from the students.

Takeaways

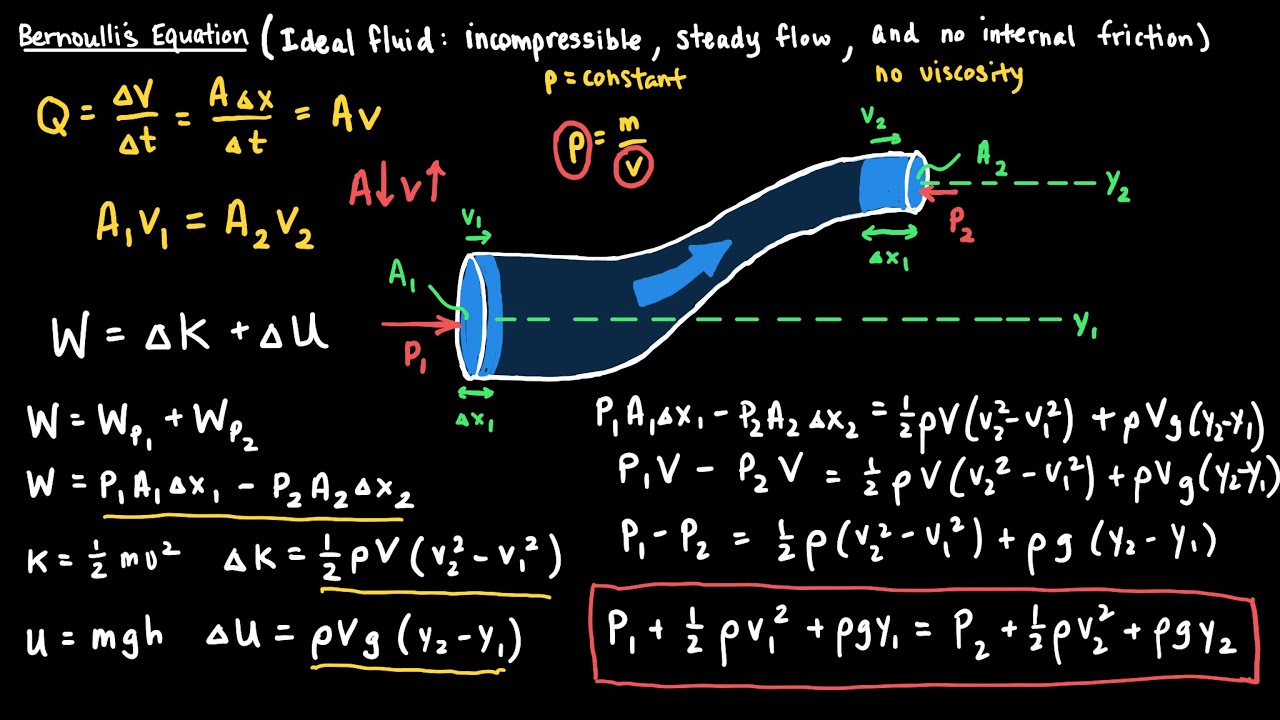
• 😀 The lesson is about the equation of momentum for steady-state flow in fluid mechanics, specifically focusing on the development of the momentum equation for a steady regime.
• 😀 Newton's Second Law, which states that force equals mass times acceleration, is discussed as a fundamental concept for understanding fluid mechanics and momentum in fluids.
• 😀 Acceleration, as the rate of change of velocity in both magnitude and direction, is a key concept. An example of circular motion is used to illustrate how velocity changes direction but not necessarily magnitude.
• 😀 The relationship between force and acceleration is explored, explaining that a force acting on a mass results in acceleration, and thus a change in the object's velocity.
• 😀 The principle of inertia is also introduced, referencing Newton's Third Law, which suggests that an object will remain in uniform motion or at rest unless acted upon by an external force.
• 😀 The force exerted by fluids on surfaces, and vice versa, is important when designing systems like pipe connections. Different types of pipe joints (e.g., PVC, threaded, and flanged) are used depending on the forces involved in the fluid flow.
• 😀 The lesson explains how high pressures and velocities in fluid systems can lead to failure at pipe joints, emphasizing the importance of proper pipe selection and joint design.
• 😀 The force equation for steady-state flow is derived by expressing the relationship between mass flow rates and velocities at different points (inlet and outlet) in a flow system, leading to the equation F = ṁ (V2 - V1).
• 😀 The equation derived expresses the net force exerted by a fluid as the difference in momentum between the inlet and outlet velocities, showing the influence of velocity changes on the forces involved in fluid flow.
• 😀 In practical applications, the force applied by the fluid to the pipe is what is of interest, as it governs the need for robust pipe connections and prevents movement or failure of the piping system under varying fluid conditions.

Q & A

What is the main topic discussed in this lecture?

The main topic of the lecture is the equation for momentum in a steady-state regime (permanent regime) in fluid mechanics.

How does Newton's Second Law relate to fluid mechanics in this context?

Newton's Second Law, which states that force equals mass times acceleration, is used to explain the relationship between force and the change in velocity of the fluid. In fluid mechanics, this concept is applied to determine the force exerted by a fluid on a surface.

What is meant by 'acceleration' in the context of fluid flow?

Acceleration in fluid flow refers to the change in velocity, either in magnitude or direction. For example, in circular motion, the fluid's velocity changes direction, which results in acceleration (centripetal acceleration).

What is the significance of mass flow rate in the momentum equation?

The mass flow rate (qm) is a key component in the momentum equation. It represents the amount of mass passing through a section of the pipe per unit of time and is used to calculate the force exerted by the fluid in the system.

How is momentum defined in fluid mechanics?

In fluid mechanics, momentum is defined as the product of mass and velocity (m × v). This quantity is important because it helps quantify the motion of the fluid and is used to calculate the forces acting on surfaces in contact with the fluid.

What does the equation F = qm × (V2 - V1) represent?

The equation F = qm × (V2 - V1) represents the force exerted by the fluid in a steady-state system, where qm is the mass flow rate, and V2 and V1 are the velocities of the fluid at two different sections of a pipe.

Why is the direction of the force related to the difference in velocities?

The direction of the force is aligned with the difference in velocities because the fluid's momentum changes as it flows through different sections of the pipe. The force acts in the direction of this change in velocity.

What role does the pipe play in the application of force to the fluid?

The pipe acts as the surface that the fluid interacts with. When the fluid changes direction (such as when flowing through a bend or curve), the pipe exerts a force on the fluid, and the fluid exerts an equal and opposite force on the pipe.

What happens if the pipe is not properly secured?

If the pipe is not securely fixed, the force exerted by the fluid can cause the pipe to be displaced or moved, potentially leading to structural damage or failure of the system.

What are the recommended textbooks for further study of fluid mechanics?

The primary textbook recommended for this course is Franco Brunet's 'Mecânica dos Fluidos.' Additional textbooks include 'Introduction to Fluid Mechanics' by Fox and McDonald, which provides more detailed and complex explanations.