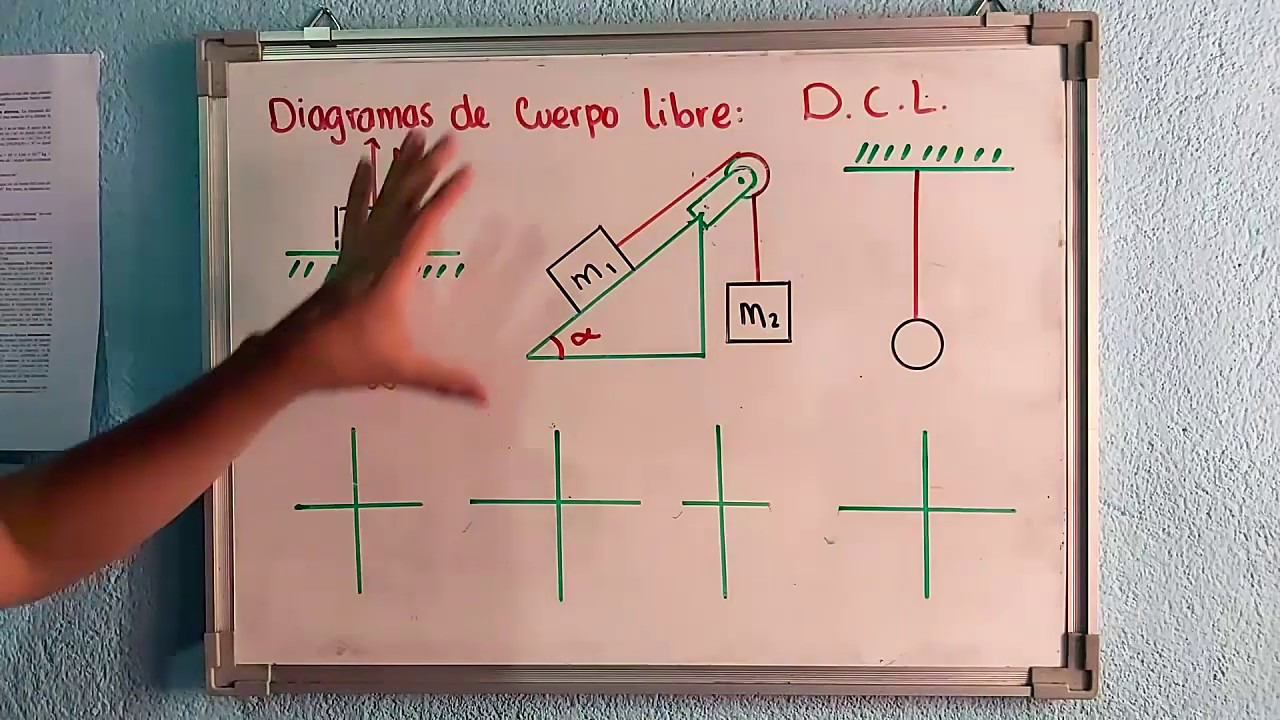
Plano inclinado con rozamiento - 2da ley de Newton

Summary

En este video, se resuelve un ejercicio de física sobre las leyes de Newton aplicado a un plano inclinado con fricción. El problema involucra dos masas conectadas por una cuerda que corre sobre una polea sin fricción. A través de diagramas de cuerpo libre y el uso de las leyes de Newton, se calcula la aceleración de las masas. Se aborda el análisis de fuerzas como la gravedad, la tensión, la fricción y las proyecciones en los ejes. Finalmente, se obtiene una aceleración de 0.60 m/s² para el sistema. El video ofrece una explicación detallada y paso a paso para resolver este tipo de problemas.

Takeaways

• 😀 En este ejercicio se trata de un sistema con dos masas conectadas por una cuerda, donde una de las masas está sobre un plano inclinado con fricción y la otra está suspendida libremente.
• 😀 La masa M1 es de 16 kg, situada sobre un plano inclinado a 30 grados, y la masa M2 es de 4 kg, suspendida verticalmente.
• 😀 El coeficiente de fricción cinético entre el bloque y el plano inclinado es de 0.2.
• 😀 El objetivo del ejercicio es calcular la aceleración de las dos masas en el sistema.
• 😀 Se asume que el sistema está en movimiento, por lo que se define la dirección de movimiento de las masas.
• 😀 Para resolver el problema, se utilizan los diagramas de cuerpo libre de las masas M1 y M2, considerando todas las fuerzas involucradas.
• 😀 En el caso de la masa M2, las fuerzas principales son el peso (hacia abajo) y la tensión en la cuerda (hacia arriba).
• 😀 En el caso de la masa M1, se analizan las fuerzas: la componente del peso en la dirección del plano inclinado, la tensión de la cuerda, y la fuerza de fricción.
• 😀 La fuerza de fricción se calcula usando el coeficiente de fricción y la fuerza normal, que es el componente del peso de M1 en la dirección perpendicular al plano.
• 😀 Finalmente, se igualan las ecuaciones de tensión para ambas masas y se resuelve para la aceleración del sistema, obteniendo un valor de 0.060 m/s².

Q & A

¿Cuál es el objetivo principal del ejercicio descrito en el video?

El objetivo principal es encontrar la aceleración de dos masas conectadas por una cuerda que corre sobre una polea sin fricción, una de las cuales se mueve sobre un plano inclinado con fricción.

¿Qué valores se nos dan para resolver el ejercicio?

Se nos da la masa de M1 (16 kg), la masa de M2 (4 kg), la inclinación del plano (30 grados), el coeficiente de fricción cinético (0.2) y la gravedad (9.8 m/s²).

¿Qué se debe hacer primero para resolver este ejercicio?

El primer paso es hacer los diagramas de cuerpo libre para cada una de las masas, donde se identifican todas las fuerzas que actúan sobre ellas.

¿Por qué se asume que M1 se mueve hacia arriba en el ejercicio?

Se asume que M1 se mueve hacia arriba para definir la dirección de la aceleración, ya que el ejercicio no especifica cuál es la dirección del movimiento.

¿Qué fuerzas actúan sobre la masa M2?

Sobre la masa M2 actúan el peso (hacia abajo), la tensión de la cuerda (hacia arriba), y la aceleración que provoca el movimiento.

¿Qué representa la proyección de los vectores peso sobre los ejes en el diagrama de cuerpo libre de M1?

Las proyecciones del vector peso sobre los ejes X y Y representan las componentes del peso de la masa M1 a lo largo del plano inclinado. Estas componentes se calculan usando el seno y coseno del ángulo de inclinación.

¿Cómo se calcula la fuerza de fricción que actúa sobre M1?

La fuerza de fricción se calcula como el producto del coeficiente de fricción (μ) y la fuerza normal, que es igual a la masa de M1 multiplicada por la gravedad y el coseno del ángulo de inclinación.

¿Por qué se utiliza la segunda ley de Newton en este ejercicio?

Se utiliza la segunda ley de Newton para establecer las ecuaciones de movimiento de las masas, donde la suma de las fuerzas en una dirección es igual a la masa de un objeto multiplicada por su aceleración.

¿Qué sucede con la tensión en la cuerda de acuerdo a las leyes de Newton?

La tensión en la cuerda es la misma en ambos lados, ya que la cuerda es ideal y no tiene fricción. Por lo tanto, la tensión en la masa M1 es igual a la tensión en M2.

¿Cuál es la ecuación final que se obtiene para calcular la aceleración?

La ecuación final para calcular la aceleración es: a = (m1 * g * sin(θ) - m2 * g - μ * m1 * g * cos(θ)) / (m1 + m2)