Physics 20: 2.3 2D Vectors

Summary

This educational video script explains the process of solving vector addition in two dimensions with vectors at angles. The presenter guides viewers through the steps of determining vector components, combining them, and calculating the resultant vector. Using an example of a person walking 15 meters at 30° north of east and then 10 meters at 20° west of north, the script demonstrates how to find the horizontal and vertical components using trigonometry, add them to find the resultant displacement, and then use the Pythagorean theorem to determine the magnitude and direction of the final vector. The method is illustrated with clear examples, making it accessible for learners to understand and apply.

Takeaways

• 📐 Today, we are solving vector problems involving two vectors in two dimensions.
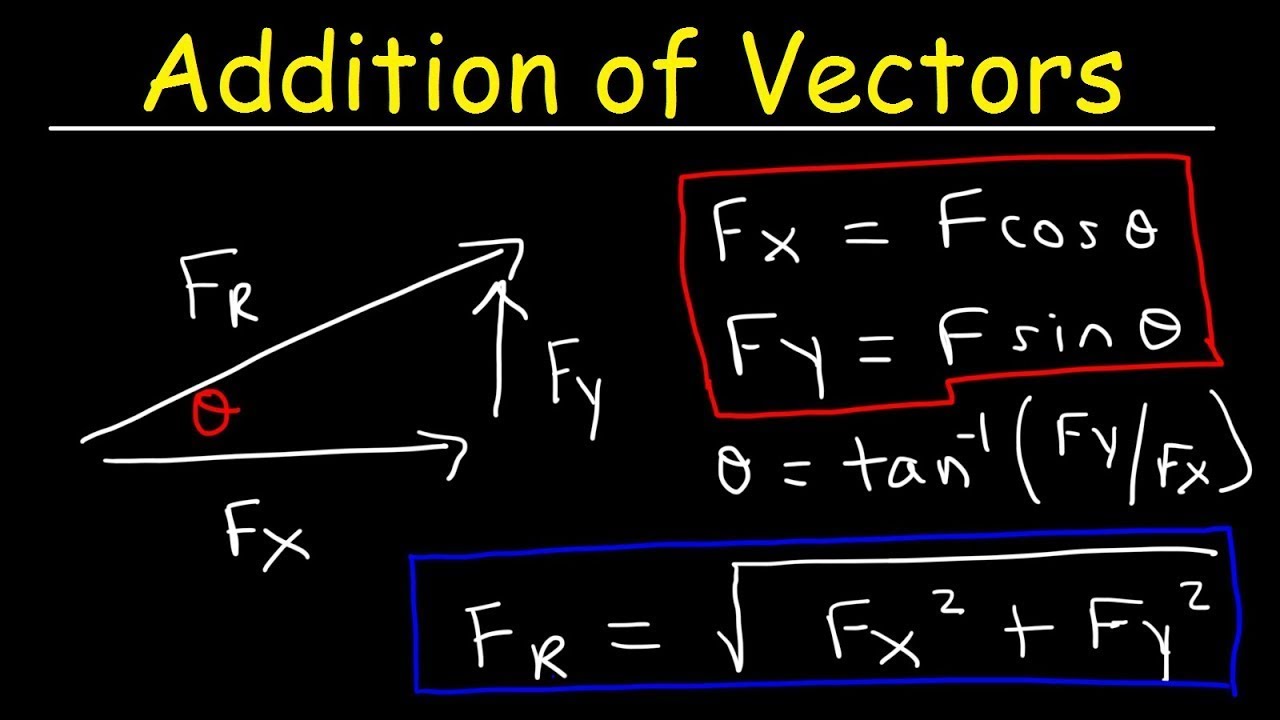
• 📊 First, break down the vectors into components to simplify the problem.
• 📝 Example problem: A person walks 15m at East 30° North and then 10m at North 20° West.
• 📏 Calculate the vertical and horizontal components of the first vector (15m at 30°).
• 📐 The vertical component is 7.5m and the horizontal component is 12.99m.
• 📏 Next, calculate the components of the second vector (10m at 20°).
• 📐 The vertical component is 9.4m and the horizontal component is 3.42m.
• 🔄 Combine the vertical components (7.5m + 9.4m = 16.9m) and the horizontal components (12.99m - 3.42m = 9.57m).
• 📐 Use the Pythagorean theorem to find the resultant vector length (19m) and angle (60°).
• ✅ Final displacement is 19m at East 60° North.

Q & A

What is the process for solving vector addition problems with two vectors in two dimensions?

The process involves breaking down the problem into steps: first, determine the vector components for each vector, then combine these components, and finally calculate the resultant vector which includes its magnitude and direction.

How does the example in the script illustrate the vector addition process?

The example demonstrates the process by showing a person walking 15 meters at 30° North of East, followed by 10 meters at 20° West of North. The script then guides through finding the horizontal and vertical components of each vector, combining them, and finally calculating the resultant vector's magnitude and direction.

What is the first step in solving for the vector components of a given vector?

The first step is to sketch the situation and determine the horizontal (x) and vertical (y) components of the vector by using trigonometric functions such as sine for the vertical component and cosine for the horizontal component.

How are the horizontal and vertical components of the first vector in the example calculated?

For the first vector, the vertical component is calculated using sin(30°) * 15 m, which equals 7.5 m. The horizontal component is calculated using cos(30°) * 15 m, which equals approximately 12.99 m.

What trigonometric functions are used to find the components of the second vector in the example?

For the second vector, sine is used to find the horizontal component (sin(20°) * 10 m), and cosine is used to find the vertical component (cos(20°) * 10 m).

How are the components of the second vector combined with the first to find the resultant vector?

The vertical components (9.4 m and 7.5 m) are added together, and the horizontal components (12.99 m to the right and 3.42 m to the left) are combined by subtracting the leftward component from the rightward component, resulting in a net horizontal component of 9.57 m to the right.

What mathematical theorem is used to find the magnitude of the resultant vector?

The Pythagorean theorem is used to find the magnitude of the resultant vector by adding the squares of the combined vertical and horizontal components and then taking the square root of the sum.

How is the direction of the resultant vector determined?

The direction of the resultant vector is determined by calculating the angle it makes with the horizontal axis, which can be found using trigonometric functions and the components of the resultant vector.

What is the final answer for the magnitude and direction of the resultant vector in the example?

The final answer for the magnitude is approximately 19.4 meters, and the direction is East 60° North.

Why is it important to break down the original vectors into their components before combining them?

Breaking down the original vectors into their components simplifies the process of vector addition, especially when the vectors are not aligned with the coordinate axes. It allows for easier calculation of the resultant vector's magnitude and direction.

Can the process demonstrated in the script be applied to vectors with different magnitudes or angles?

Yes, the process can be applied to vectors with different magnitudes or angles. The key is to calculate the horizontal and vertical components for each vector and then combine and recalculate the resultant vector accordingly.

Outlines

00:00

📚 Introduction to Solving Vector Addition in Two Dimensions

This paragraph introduces the concept of solving vector addition problems in two dimensions where vectors are at specific angles, making the calculations more complex. The speaker outlines the process of breaking down the problem into manageable steps: identifying vector components, combining them, and determining the resultant vector. An example is presented where a person walks 15 meters east at 30° north and then 10 meters at 20° west of north. The goal is to find the final displacement and direction. The speaker emphasizes the importance of sketching the situation and calculating the vertical and horizontal components of each vector using trigonometric functions like sine and cosine. The first vector's components are calculated as 12.99 meters east and 7.5 meters north.

05:00

🔍 Calculating Components and Resultant Vector for Two Vectors

In this paragraph, the process continues with the calculation of the second vector's components. The horizontal component is found using the sine of the angle (20°), resulting in 3.42 meters to the west, and the vertical component using the cosine of the angle (20°), resulting in 9.4 meters upward. The speaker then combines the vertical components of both vectors, summing 9.4 meters and 7.5 meters to get a total upward displacement of 16.9 meters. For the horizontal components, the eastward displacement (12.99 meters) is adjusted by subtracting the westward displacement (3.42 meters), yielding a net eastward displacement of 9.57 meters. The final step involves using the Pythagorean theorem to find the magnitude of the resultant vector, which is approximately 19.43 meters, and calculating the direction, which is found to be 60° north of east. The paragraph concludes with the final answer presented in vector notation, rounded to two decimal places.

Keywords

💡Vector Components

Vector components refer to the individual horizontal and vertical parts of a vector when it is decomposed in a two-dimensional space. In the video, the concept is used to break down the complex motion of a person walking at specific angles into simpler, easier-to-manage parts. For example, the person walks 15 meters at 30° North of East, which is then decomposed into a vertical component (7.5 meters North) and a horizontal component (12.99 meters East).

💡Resultant Vector

The resultant vector is the single vector that represents the combined effect of two or more vectors acting together. In the context of the video, after determining the individual components of the vectors representing the person's walk, the resultant vector is calculated by adding the vertical components and subtracting the horizontal components due to their opposite directions. This gives the final displacement and direction of the person's walk.

💡Trigonometry

Trigonometry is a branch of mathematics that deals with the relationships between the sides and angles of triangles. The video uses trigonometric functions, such as sine and cosine, to calculate the vertical and horizontal components of the vectors. For instance, the vertical component is found using sin(30°) * 15 meters, and the horizontal component is found using cos(30°) * 15 meters.

💡Pythagorean Theorem

The Pythagorean theorem is a fundamental principle in geometry that states the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. In the video, the theorem is applied to find the magnitude of the resultant vector by adding the squares of the vertical and horizontal components and then taking the square root of the sum.

💡Displacement

Displacement in physics refers to the change in position of an object. It is a vector quantity that has both magnitude and direction. In the video, the person's final displacement is calculated by determining the resultant vector after the person has walked in two different directions with specific angles and magnitudes.

💡Direction

Direction in this context refers to the orientation of the resultant vector, which indicates the angle at which the object has moved from its starting point. The video explains how to find the direction of the resultant vector by using the calculated components and applying trigonometric relationships.

💡Angles

Angles are a measure of rotation and are crucial in determining the direction of vectors. In the script, angles such as 30° North of East and 20° West of North are given to specify the direction of the person's walk. These angles are used to decompose the vectors into their components and later to find the resultant vector's direction.

💡Horizontal Component

The horizontal component of a vector is the part of the vector that acts parallel to the ground or along the x-axis in a two-dimensional coordinate system. In the video, the horizontal component is calculated for each vector to find how far the person moves east or west.

💡Vertical Component

The vertical component of a vector is the part of the vector that acts perpendicular to the ground or along the y-axis in a two-dimensional coordinate system. In the video, the vertical component is calculated to determine how far the person moves north or south.

💡Sine and Cosine Functions

Sine and cosine are trigonometric functions used to relate the angles of a right triangle to the lengths of its sides. In the video, sine is used to find the vertical component (opposite side), and cosine is used to find the horizontal component (adjacent side) of the vectors.

Highlights

Introduction to solving vector component questions with two vectors in two dimensions.

First step: figure out the vector components and then combine them.

Example problem: adding vectors 15 meters at East 30° North and 10 meters at North 20° West.

Sketching the situation to visualize the problem.

Finding the resultant displacement and direction.

Breaking down the vectors into vertical and horizontal components.

Calculating the components using trigonometric functions: sine and cosine.

Summing up vertical components: 7.5 (first vector) + 9.4 (second vector) = 16.9.

Calculating the horizontal components: 12.99 (first vector) - 3.42 (second vector) = 9.57.

Using Pythagorean theorem to find the resultant vector's magnitude: 19.43.

Finding the angle of the resultant vector: 60°.

Stating the final vector in terms of magnitude and direction: 19 meters at East 60° North.

Second example problem: 25 meters/second at an angle of 40° from Northwest.

Second vector: 30 meters/second straight South.

Repeating the process of breaking into components and solving.

Transcripts

okay today we're going to look at

solving Vector com questions that have

uh two vectors in two Dimensions so both

of them are going at Angles so that

makes things a little more complicated

but what we have to do is we just have

to break it down into a couple of steps

where we do exactly what we did before

so we're going to first of all figure

out what the vector components are and

then we're going to combine those and

then figure out what the resultant would

be so the best way to show this is just

to start with an example so let's do

that so let's our question is so a

person walks 15

M

at so let's suppose we want to add 15

M at uh

East 30°

north and then let's say they're going

to go 10 m after

that

at

North

20° West okay so the question is what is

the resultant what is our final

displacement and Direction so for all

these questions you want to find the

length of the vector plus the

direction okay so our first the first

thing is let's sketch out this this

situation so let's suppose we started at

the bottom here so we're going to go at

30

Dees okay so we know it's going to be

30° from east to North nor and this was

15 and then afterwards the second Vector

we're going to go from head to tail so

we're going to start the second one and

it's going to go something like

that right where this is

20° and that one's going to go 10 so the

question then is what is the resultant

so our resultant would be from

start to finish okay so for us to try to

do this with trigonometry it's a little

bit difficult because we don't know all

the angles we don't know whether it's a

right angle triangle or not so the best

bet is to first step is to figure out

the components so if we look at just

that first Vector the

15 the first thing you want to do is

figure out the vertical and horizontal

components of of that vector by itself

okay so we know it's 30° we know it's 15

so we can easily solve for each of those

so our vertical side because the Y is

the opposite so you'd have S of 30

equals opposite over

15 and we can do that on our calculator

so just go sin

30 time 15 so that'll give us

7.5 okay so we know that that side is

7.5 and then we want to do the same

thing for the bottom but the bottom this

time is adjacent so we'd have cosine of

30 = x over

15 so do that one on your calculator

go cos 30 *

15 and that gives us

12.99 we'll leave the decimals intact

for now we'll round off at the end okay

so 12.99 so we've got our two sides of

that initial triangle let me write those

in there so we have 12.99 to the East

and then our vertical component was 7.5

to the

north okay so now what we want to do is

basically repeat the exact same thing

using the second triangle so our second

triangle we're going to have a vertical

component that goes up first and then

our horizontal goes to the left okay so

we want to basically do the exact same

thing okay so we want to find the

horizontal and vertical components in

this case the horizontal is our opposite

side

so we'd

have sin

20 okay so we got the opposite side so

sin 20 would equal x over 10 and then

the same thing for the vertical

component but it'll be cosine because

it's our adjacent so cos 20 = y/ 10 so

that's our calculations we need for the

second triangle so let's solve for each

of those So Co or that's to the S 21st

so s 20 *

10 gives us

3.42 and then do cos 20 *

10 gives us

9.4 if we round it

off okay so let's write those on our

original triangle again so we have 3

42 on the

top and 9.4 on the

side and that's it so we've got our

triangles calculated so we figured out

all the components for the two vectors

so now when you look at it you can see

basically what we do have is we have two

vectors that go up right we have our two

vertical vectors so if we can combine

those two into one so let's just make

one tall Vector that goes up and it'll

be

9.40 plus 7.5 cuz they're both going

upward so we can add them together so

that would be the same thing as

[Music]

16.9 and then if you look at the

horizontal vectors we got 12.99 to the

right but then we have

3.42 going to the left so because those

are in opposite directions we need to

subtract them so

12.99 - 3.42 2 gives us an answer of

9.57 to the right that's the bigger

Direction okay so what we want to do

then let's just put the two vectors head

to tail it doesn't matter whether I drew

it like this or I could draw the 9.57

starting up here and go this way it

really doesn't make any difference I

just picked the bottom because that's

going to look similar to our original

right so now the question is what is the

resultant so we want to find out what

that side and angle is okay so when you

look at these two triangles you can see

that our original resultant right there

should be the exact same as the green

resultant that we're going to solve for

now okay so all we have to do for the

green one is just like we did with the

other questions find that length and

that angle and we're done so the length

is pretty easy we just use Pythagorean

theorem so 16.9 SAR + 9.57

squar and square root that answer

that gives us

[Music]

19.429661

[Music]

that and we get an angle of

60° so that's it we've done the question

so the final step then would be just to

State your answer so we'll just State

our answer in final Vector notation and

let's round it off to two digits

everything should be in two digits so

our final answer was 19 M right the 19.4

we'll round it to two and our Direction

was 60° so we went East

60°

North and that's it okay so you can see

with this question we sort of did two

steps First Step was break the original

vectors into its two components then

combine those into one new triangle and

then solve that new triangle for the

hypotenuse and the

angle let's try one more and that'll be

it for today so let's suppose in this

case I've got a vector that

goes 25 m/ second at an angle

[Music]

of let's suppose that angle is 40° from

Northeast or north west and then let's

suppose our second Vector then

goes

down

at um let's say it's 30

m/s and that one is straight South okay

so this one is perfectly so the other

one was at an angle of

40° so we want to do the exact same

thing again so let's break it into our

horizontal and vertical

components so that first first Vector

we'll just do those two