How many ways are there to prove the Pythagorean theorem? - Betty Fei
Summary
TLDRThis video explores the Pythagorean theorem, its historical significance, and various proofs. The theorem, attributed to Pythagoras, states that in a right triangle, the square of the two shorter sides equals the square of the hypotenuse. The script traces its origins from Babylonian and Egyptian mathematicians, through ancient Indian texts, and highlights different ways to prove the theorem. It presents several proofs, including those by Pythagoras, Euclid, and even a twelve-year-old Einstein. With over 350 known proofs, the video encourages viewers to discover their own contribution to this timeless mathematical truth.
Takeaways
- 😀 The Pythagorean theorem states that for a right triangle, the square of one side plus the square of the other side equals the square of the hypotenuse (a² + b² = c²).
- 😀 The Pythagorean theorem is fundamental in geometry and has practical applications like constructing stable buildings and triangulating GPS coordinates.
- 😀 The theorem is named after Pythagoras, a Greek mathematician, but was known more than a thousand years earlier by the Babylonians and Egyptians.
- 😀 A Babylonian tablet from 1800 B.C. lists 15 sets of numbers that satisfy the Pythagorean theorem, showing its ancient roots.
- 😀 Ancient Egyptian surveyors possibly used the 3-4-5 triangle to create square corners for surveying, utilizing the Pythagorean theorem.
- 😀 The earliest Indian mathematical texts (800-600 B.C.) describe the relationship between the sides of a square and its diagonal, based on the Pythagorean theorem.
- 😀 Proofs are essential in mathematics, using existing rules and logic to demonstrate a theorem's validity for all cases.
- 😀 One classic proof of the Pythagorean theorem involves rearranging identical right triangles to show that a² + b² = c².
- 😀 Euclid and a twelve-year-old Einstein independently arrived at another proof, dividing a right triangle and using similar triangles to derive the theorem.
- 😀 Tessellation, or repeating geometric patterns, can be used to visually prove the Pythagorean theorem by showing how areas correspond.
- 😀 The Pythagorean theorem has over 350 proofs, ranging from well-known to obscure, demonstrating its mathematical significance and versatility.
Q & A
What is the Pythagorean theorem?
-The Pythagorean theorem states that for a right triangle, the square of one side plus the square of the other side is equal to the square of the hypotenuse. In mathematical terms, a² + b² = c².
Who are some of the figures associated with proving the Pythagorean theorem?
-Euclid, twelve-year-old Einstein, and American President James Garfield are among those who came up with elegant proofs for the Pythagorean theorem.
What are some real-life applications of the Pythagorean theorem?
-The Pythagorean theorem is fundamental for constructing stable buildings and triangulating GPS coordinates.
How was the Pythagorean theorem known before Pythagoras?
-The Pythagorean theorem was known over a thousand years before Pythagoras, as evidenced by a Babylonian tablet from around 1800 B.C. listing 15 sets of numbers that satisfy the theorem.
How did ancient Egyptians possibly use the Pythagorean theorem?
-Ancient Egyptian surveyors may have used a set of numbers, 3, 4, and 5, to make square corners by stretching a knotted rope with twelve equal segments to form a right triangle.
What is the converse of the Pythagorean theorem?
-The converse of the Pythagorean theorem states that if a triangle’s sides satisfy the equation a² + b² = c², then it must be a right triangle.
What was the key mathematical insight from Indian mathematical texts about the Pythagorean theorem?
-Indian mathematical texts written between 800 and 600 B.C. described how stretching a rope across the diagonal of a square results in a square twice the size of the original one, a relationship that can be derived from the Pythagorean theorem.
What is proof by rearrangement in relation to the Pythagorean theorem?
-Proof by rearrangement is a strategy where four identical right triangles are arranged into a square and then rearranged into rectangles. The total area remains the same, showing that c² = a² + b².
How does Euclid’s proof of the Pythagorean theorem work?
-Euclid’s proof involves dividing a right triangle into two smaller triangles and using the principle that corresponding angles of similar triangles result in proportional sides, ultimately proving the Pythagorean theorem.
What is a tessellation-based proof of the Pythagorean theorem?
-A tessellation-based proof visually demonstrates the Pythagorean theorem by using repeating geometric patterns, where the area of one square (a²) plus another (b²) equals the area of the largest square (c²).
How can a physical model demonstrate the Pythagorean theorem?
-A turntable with three square boxes of equal depth can demonstrate the theorem. By filling the largest square with water and spinning the turntable, the water will perfectly fill the two smaller squares, showing that the areas are equivalent.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Pythagoras (1) - Pengenalan Teorema Pythagoras, Pythagoras Theorem - Matematika SMP

TRIPEL PYTHAGORAS - TEOREMA PYTHAGORAS (3) - MATEMATIKA SMP KELAS 8
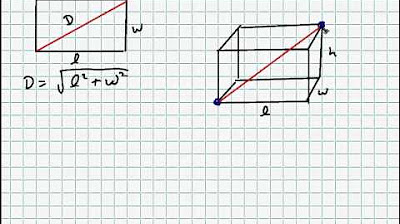
The Pythagorean Theorem: Extensions and Applications

LSU Number Theory Lecture 04 sumprod
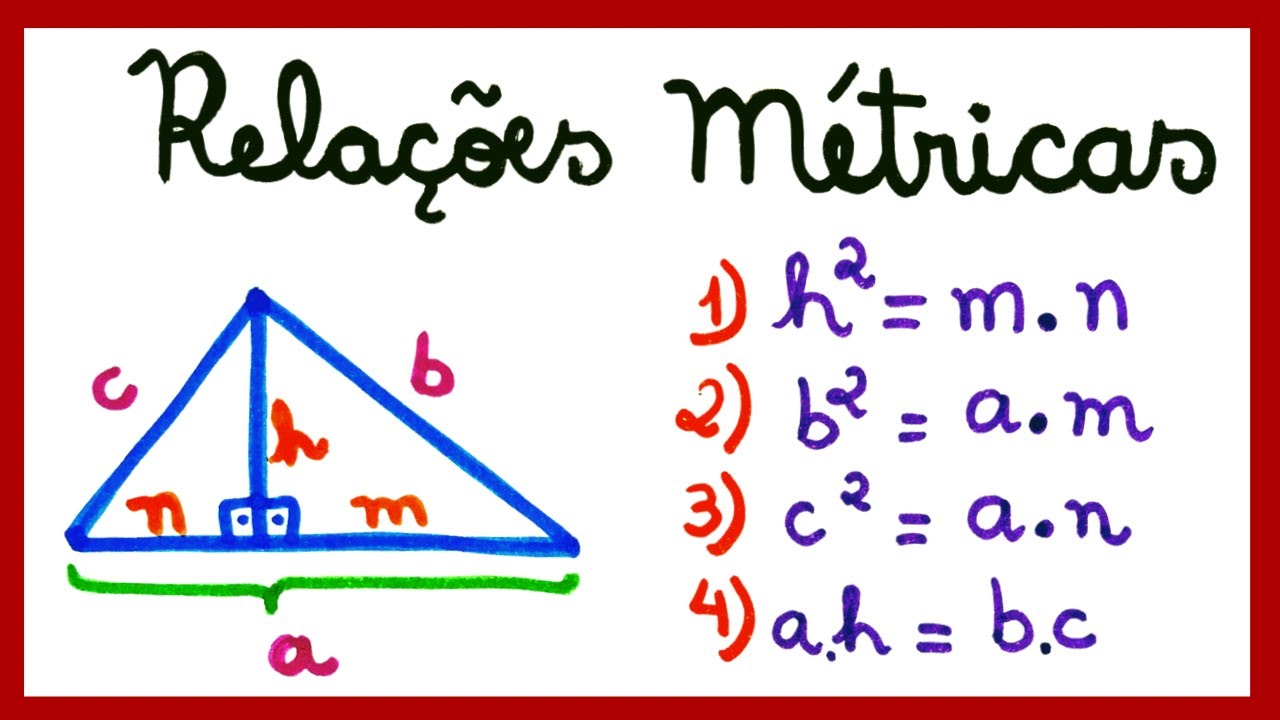
RELAÇÕES MÉTRICAS NO TRIÂNGULO RETÂNGULO!!

Geometry – 7.1 Pythagorean Theorem and Its Converse
5.0 / 5 (0 votes)