Graus e radianos

Summary

This educational script introduces the concepts of degrees and radians, explaining their roles as units of angular measurement. The speaker demonstrates how to convert between degrees and radians, using examples and emphasizing the proportional relationship between an angle and the arc length it subtends. The video also covers how to calculate the length of an arc based on the central angle and provides intuitive methods to understand these formulas. Lastly, common conversions between degrees and radians are outlined to help students grasp these essential trigonometric concepts easily.

Takeaways

• 😀 A degree is a unit of angular measurement, where 360° represents a full circle, and each degree is 1/360th of the circle.
• 😀 A radian is defined as the angle subtended by an arc whose length is equal to the radius of the circle.
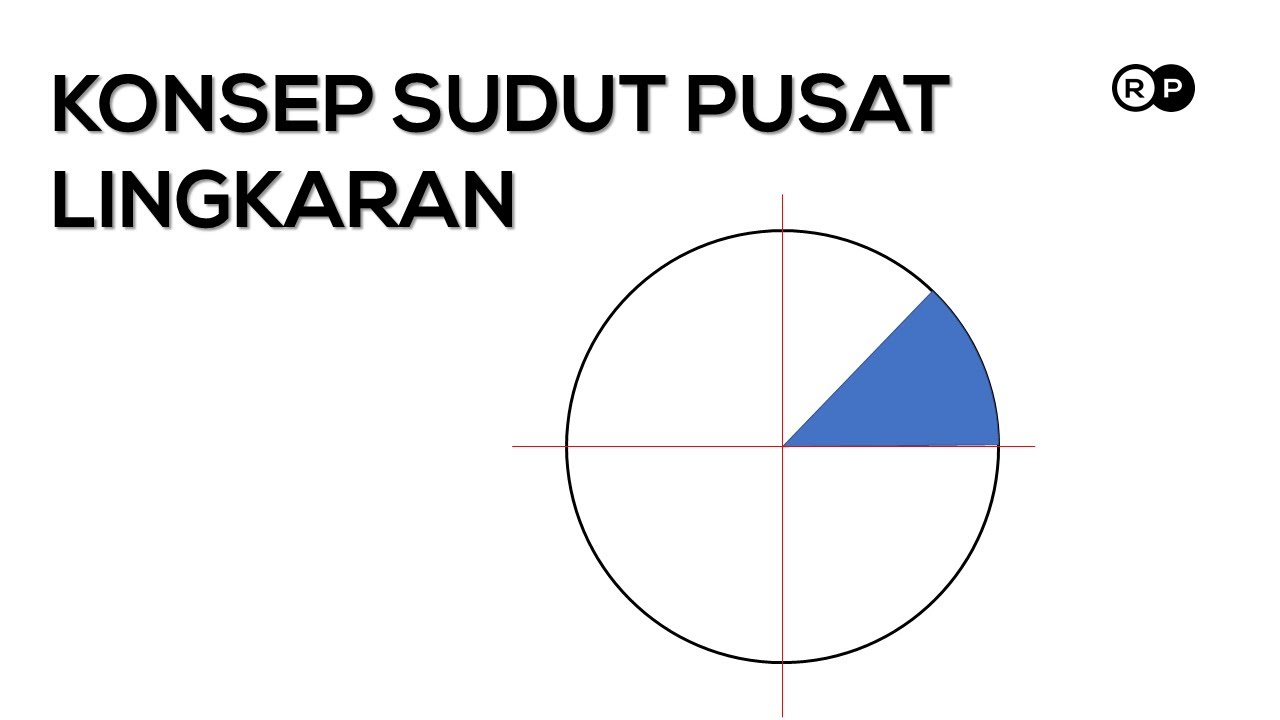
• 😀 The central angle of a circle is an angle whose vertex is at the center, and it subtends an arc. The degree measure of the central angle is equal to the degree measure of the arc.
• 😀 To find the length of an arc, the formula is: Length of arc = (Alpha / 360°) * 2πr, where Alpha is the central angle in degrees and r is the radius of the circle.
• 😀 A radian is related to the radius of the circle. If the length of an arc equals the radius, the central angle is one radian.
• 😀 The circumference of a circle is 2πr, and it is equivalent to 360° or 2π radians.
• 😀 The conversion between degrees and radians is: To convert degrees to radians, multiply by π/180°, and to convert radians to degrees, multiply by 180°/π.
• 😀 Key angle conversions: 180° = π radians, 90° = π/2 radians, 60° = π/3 radians, 45° = π/4 radians, and 30° = π/6 radians.
• 😀 One radian is the angle subtended by an arc whose length equals the radius of the circle, and 360° corresponds to 2π radians.
• 😀 Memorizing key angle conversions can help simplify trigonometric calculations, as certain angles appear frequently in problems.

Q & A

What are degrees and radians, and how are they related to the circumference?

Degrees and radians are units of angular measurement. Degrees are commonly known, with a full circle divided into 360 degrees. A radian, on the other hand, is defined as the angle subtended by an arc whose length is equal to the radius of the circle. The full circumference of a circle equals 360 degrees or 2π radians.

What is a central angle, and how does it relate to an arc on the circle?

A central angle is an angle whose vertex is at the center of the circle. The angle corresponds to an arc on the circle, and the degree measure of that angle is equal to the degree measure of the arc it subtends.

How can we calculate the length of an arc on a circle?

The length of an arc can be found by multiplying the total circumference (2πr) by the fraction of the circle represented by the angle. Specifically, the length of the arc (L) is given by L = (α/360) × 2πr, where α is the central angle in degrees.

What is the relationship between the central angle and the arc length?

The central angle and the arc length are directly proportional. The length of an arc is proportional to the angle subtended by that arc, with the circumference representing a full circle.

How is the length of an arc calculated using the central angle and radius?

To calculate the length of an arc, use the formula L = (α/360) × 2πr, where α is the central angle in degrees and r is the radius of the circle. This formula assumes the angle is measured in degrees.

What is a radian, and how is it defined?

A radian is a unit of angular measurement where the central angle subtended by an arc whose length is equal to the radius of the circle is defined as 1 radian. It connects angular measurement directly to the radius of the circle.

What is the conversion between radians and degrees?

The conversion between radians and degrees is based on the equivalence that 2π radians is equal to 360 degrees. Therefore, to convert from radians to degrees, multiply by (360/2π), and to convert from degrees to radians, multiply by (π/180).

How many radians are in a full circle?

A full circle contains 2π radians, which is approximately 6.28 radians. This corresponds to the 360 degrees of a full circle.

What is the value of one radian in degrees?

One radian is approximately equal to 57.3 degrees. This is derived from the ratio between the total number of degrees in a circle (360°) and the number of radians in a circle (2π).

Why is it important to understand both degrees and radians in trigonometry?

Understanding both degrees and radians is important because they are used interchangeably in various areas of trigonometry. Radians are especially useful in calculus and other advanced mathematical fields, while degrees are more commonly used in everyday applications and initial geometry problems.