Konversi Sudut - Ukuran Derajat - Konversi Radian ke Derajat dan Sebaliknya - Trigonometri Part 3
Summary
TLDRThis educational video explains the conversion of angles in trigonometry, focusing on converting between degrees, minutes, seconds, and radians. The instructor demonstrates the relationship between these units using practical examples, such as converting 12.7 degrees into degrees, minutes, and seconds, as well as converting between radians and degrees. The video also covers key formulas, such as converting degrees to radians and vice versa. With clear visuals and step-by-step explanations, the content makes these mathematical concepts easy to understand for viewers interested in trigonometric angle conversions.
Takeaways
- 😀 Degrees and radians are two units used to measure angles, and conversion between them is a fundamental concept in trigonometry.
- 😀 One full rotation (360°) is equivalent to 2π radians, and each degree is 1/360th of a full rotation.
- 😀 1 degree equals 60 minutes, and 1 minute equals 60 seconds, creating the system of degrees, minutes, and seconds.
- 😀 Example: To convert 12.7 degrees into degrees, minutes, and seconds, the calculation results in 12° 42' 0".
- 😀 To convert from minutes to seconds, multiply the number of minutes by 60 (e.g., 0.8 minutes equals 48 seconds).
- 😀 To convert 36.403 degrees into degrees, minutes, and seconds, the result is 36° 25' 48".
- 😀 The relationship between degrees and radians is crucial: 180° equals π radians, meaning degrees can be converted to radians by multiplying by π/180.
- 😀 To convert radians to degrees, multiply the radians by 180/π. For example, 3/5 π radians equals 108°.
- 😀 Converting 135° to radians involves dividing the degree value by 180 and then multiplying by π, yielding 3/4 π radians.
- 😀 When converting radians to degrees, using fractions of π simplifies the process (e.g., 1/3 π radians equals 60°).
Q & A
What is the relationship between degrees and a full circle?
-One full circle is equivalent to 360 degrees. This means that 1 degree is 1/360 of a complete rotation.
How are minutes and seconds used in angular measurement?
-In angular measurement, 1 degree is equal to 60 minutes, and 1 minute is equal to 60 seconds. So, 1 degree is equivalent to 3600 seconds.
How do you convert a decimal degree to degrees, minutes, and seconds?
-To convert a decimal degree to degrees, minutes, and seconds, first separate the degree part. Then, multiply the decimal part by 60 to find the minutes. If there is still a decimal, multiply that by 60 again to get the seconds.
How do you convert minutes and seconds back into decimal degrees?
-To convert minutes and seconds into decimal degrees, divide the minutes by 60 and the seconds by 3600, then add all the values together with the degrees.
What is a radian, and how is it related to a degree?
-A radian is the angle subtended by an arc whose length is equal to the radius of the circle. The relationship between degrees and radians is that 180 degrees equals π radians.
How do you convert radians to degrees?
-To convert radians to degrees, multiply the radian value by 180 and divide by π.
How do you convert degrees to radians?
-To convert degrees to radians, multiply the degree value by π and divide by 180.
What is the formula to convert an angle from degrees to radians?
-The formula to convert an angle from degrees to radians is: Radians = Degrees × (π / 180).
What is the formula to convert an angle from radians to degrees?
-The formula to convert an angle from radians to degrees is: Degrees = Radians × (180 / π).
How do you calculate the value of radians for a given angle in degrees?
-To calculate the radians for a given angle, multiply the angle in degrees by π and divide by 180. For example, 60° = 60 × π / 180 = π/3 radians.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Trigonometri Matematika Kelas 10 • Part 1: Ukuran Sudut Derajat dan Radian
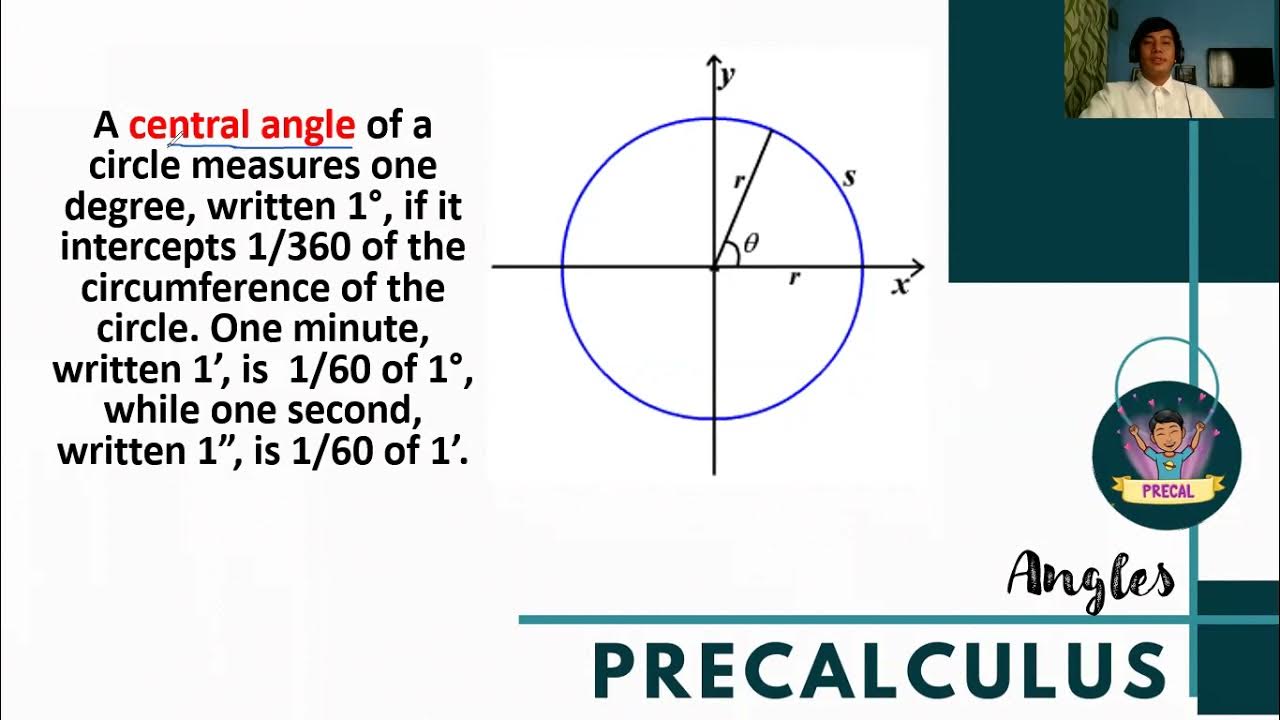
Angle Measure (Precalculus)
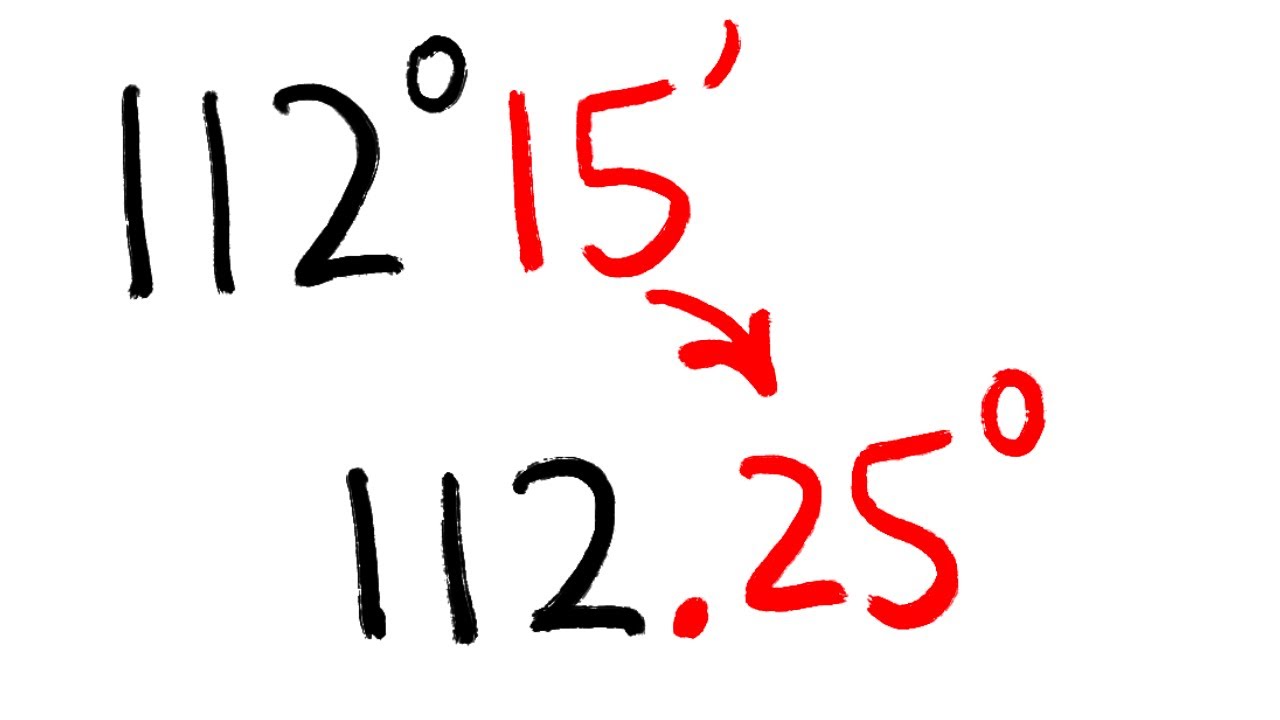
Convert degrees, minutes, and seconds (dms) into decimal degrees

Penjumlahan dan Pengurangan Sudut

Garis dan Sudut (2) | Satuan Sudut | Matematika Kelas 7

Belajar Matematika Dengan Mudah - Perbandingan Trigonometri Dalam Segitiga Siku-siku.
5.0 / 5 (0 votes)