Memahami Perbedaan Uji Multikolinieritas, Heteroskedastisitas, Autokorelasi, dan Normalitas
Summary
TLDRThis video tutorial explains the key assumptions in linear regression analysis using Ordinary Least Squares (OLS) and how to test them. It covers the detection of multicollinearity, heteroskedasticity, autocorrelation, and normality in regression models. Multicollinearity is tested through correlation and variance inflation factor (VIF). Heteroskedasticity is examined using graphical methods and various tests like Goldfeld-Quandt and Glejser. Autocorrelation is relevant for time-series data, and the Durbin-Watson test is often used. Finally, normality of residuals is checked using methods like the Kolmogorov-Smirnov test. The tutorial provides useful insights into how to ensure the validity of regression results.
Takeaways
- 😀 The video introduces various tests used in linear regression analysis, such as multicollinearity, heteroskedasticity, autocorrelation, and normality tests.
- 😀 Multicollinearity occurs when there is a strong correlation between independent variables. Examples include land size and fertilizer requirements.
- 😀 To check for multicollinearity, you can use correlation between independent variables or calculate the Variance Inflation Factor (VIF). A VIF less than 10 indicates no multicollinearity.
- 😀 Heteroskedasticity refers to non-constant variance in the error terms of the regression model, and it violates assumptions if present.
- 😀 Tests for heteroskedasticity include graphical methods, the Goldfeld-Quandt test, and the Glejser test.
- 😀 Autocorrelation occurs in time-series data when residuals from one period correlate with residuals from the previous period.
- 😀 Autocorrelation can be tested using the Durbin-Watson test, and the ideal scenario is to have no autocorrelation.
- 😀 The assumption for linear regression using OLS is that residuals follow a normal distribution.
- 😀 The normality of residuals can be tested using the Kolmogorov-Smirnov test or by visually inspecting a normality curve.
- 😀 The video encourages viewers to subscribe and like the content for more tutorials on regression analysis and related tests.
Q & A
What is the assumption of multicollinearity in OLS regression?
-The assumption of multicollinearity in Ordinary Least Squares (OLS) regression is that there should be no strong correlations between the independent variables used in the regression equation. Strong correlations can distort the regression results.
How can multicollinearity be detected in a regression analysis?
-Multicollinearity can be detected by checking the correlation between independent variables or using the Variance Inflation Factor (VIF). A VIF value greater than 10 suggests a high correlation, indicating potential multicollinearity.
What are some examples of variables that might cause multicollinearity?
-Examples include variables like land area and fertilizer use in agricultural production. These variables are often correlated because as land area increases, the need for fertilizer also rises.
What is heteroskedasticity and how does it affect regression analysis?
-Heteroskedasticity occurs when the variance of the residuals (errors) is not constant across observations. It violates the assumption of constant variance in OLS regression, potentially leading to inefficient estimates and biased inference.
How can heteroskedasticity be detected in regression analysis?
-Heteroskedasticity can be detected through graphical methods, such as plotting residuals against predicted values, or through formal tests like the Goldfeld-Quandt test or the Glejser test.
What is the purpose of testing for autocorrelation in time-series data?
-Autocorrelation tests are used to check if the residuals from one time period are correlated with residuals from previous periods. In OLS regression, the assumption is that there should be no autocorrelation among residuals.
Which test is commonly used to detect autocorrelation?
-The Durbin-Watson test is commonly used to detect autocorrelation in time-series data. It helps determine whether residuals are correlated across different time periods.
What is the assumption of normality in OLS regression, and why is it important?
-The normality assumption in OLS regression states that the residuals of the model should be normally distributed. This assumption is crucial for valid hypothesis testing and confidence interval estimation.
How can normality of residuals be tested in OLS regression?
-Normality can be tested using graphical methods, such as a Q-Q plot, or statistical tests like the Kolmogorov-Smirnov test, which compares the distribution of residuals to a normal distribution.
Why is it important to check for these classical assumption tests (multicollinearity, heteroskedasticity, autocorrelation, normality) in regression analysis?
-Checking these assumptions is important because violations can lead to biased, inconsistent, or inefficient estimates. By ensuring that the assumptions are met, the regression results become more reliable and valid for inference.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Regresi Linear Sederhana dengan Ordinary Least Square
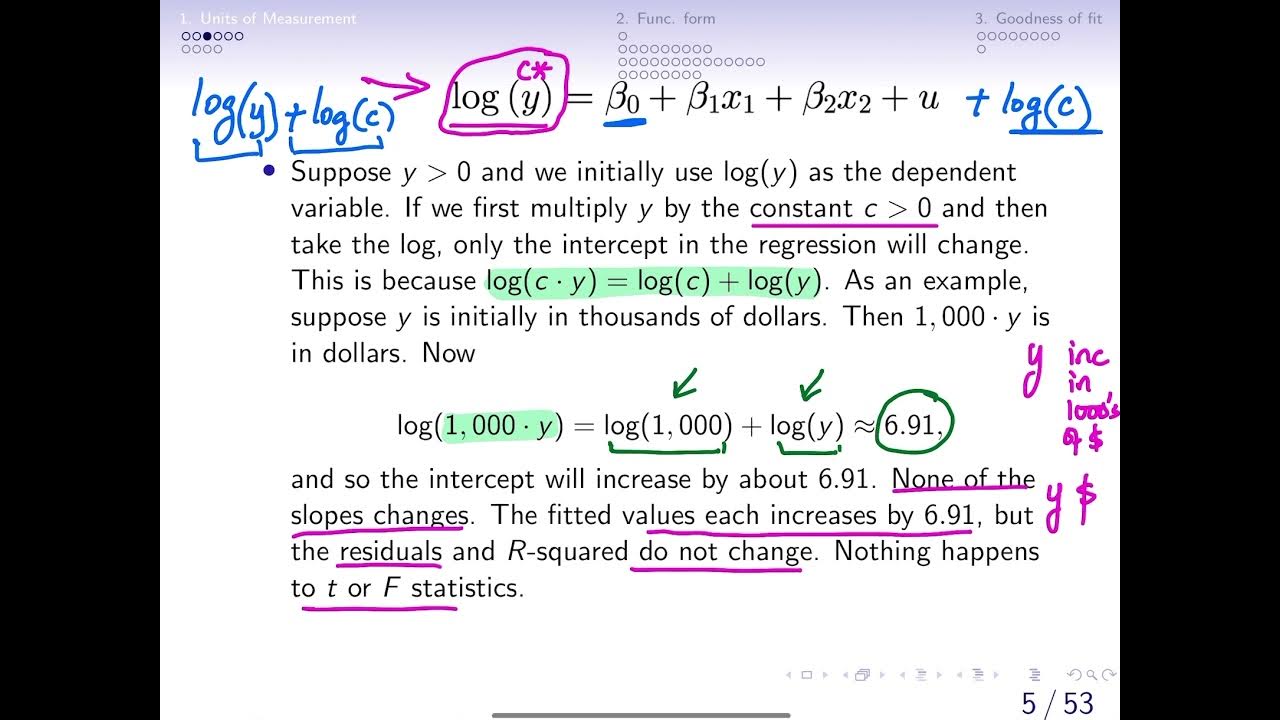
6.1 Effects of Data Scaling on OLS statistics (changing units of measurement)
Week 6 Statistika Industri II - Analisis Regresi (part 1)

Metode Statistika | Analisis Regresi Linier | Part 1 Menentukan Persamaan Regresi

Cara Menghitung Analisis Regresi Sederhana secara Manual

Metode Kuadrat Terkecil Hal 97-101 Bab 3 STATISTIK Kelas 11 SMA Kurikulum Merdeka
5.0 / 5 (0 votes)