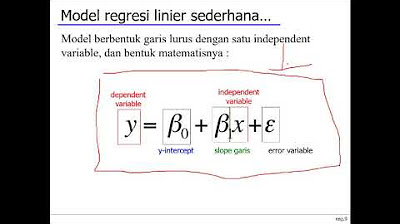
6.1 Effects of Data Scaling on OLS statistics (changing units of measurement)
Summary
TLDRThis chapter delves into multiple linear regression analysis, focusing on the effects of scaling data on Ordinary Least Squares (OLS) statistics. It explains how changing the measurement units for dependent and independent variables influences coefficients while maintaining interpretation. Key topics include the implications of logarithmic transformations, the constancy of R-squared values, and the robustness of statistical inference. Practical applications are illustrated using a dataset on birth weight, highlighting the effects of maternal smoking and family income. Overall, the content emphasizes the importance of understanding variable scaling in regression analysis.
Takeaways
- 📊 Scaling data affects OLS statistics, including coefficients and intercepts, but does not change the interpretation of the regression line.
- 🔍 Multiplying the dependent variable by a constant results in all coefficients being multiplied by that constant.
- 📈 When the dependent variable is scaled, fitted values and residuals are also multiplied by the same constant.
- ⚖️ The R-squared value remains unchanged regardless of scaling operations on the dependent variable.
- 🔄 Changing the independent variable affects the coefficients differently; they are divided by the scaling constant, maintaining interpretation.
- 📉 Fitted values and residuals remain unchanged when independent variables are scaled, and R-squared is not affected.
- 🔍 Scaling the dependent variable logarithmically alters the intercept but not the slope coefficients.
- 💡 When using logarithmic transformations, changes to the dependent variable add a constant to the intercept, impacting its value.
- 🧮 In log-linear models, changing independent variables affects the intercept but not the coefficients, preserving relationships.
- 📚 The chapter will demonstrate these principles with empirical data, focusing on birth weight as influenced by maternal smoking and family income.
Q & A
What are the main topics covered in the chapter on multiple linear regression analysis?
-The chapter discusses the effects of scaling data on OLS statistics, functional forms, and goodness of fit measures, as well as how to select regressors.
How does scaling the dependent variable affect the coefficients in a regression model?
-Scaling the dependent variable by a non-zero constant multiplies all coefficients, including the intercept and slope coefficients, by that constant.
What remains unchanged when the dependent variable is scaled?
-The R-squared value, fitted values, residuals, and t-statistics remain unchanged when scaling the dependent variable, unless the scaling factor is negative.
What happens when an independent variable is scaled?
-When an independent variable is multiplied by a constant, the corresponding coefficient is divided by that constant, but fitted values, residuals, and R-squared remain unchanged.
How do logarithmic transformations affect regression models?
-When scaling a variable in a log-linear model, the intercept is adjusted by adding the logarithm of the scaling factor, while the slope coefficients remain the same.
What is the significance of using log transformations in regression analysis?
-Log transformations help in measuring elasticities that are free of units of measurement and can approximate proportional or percentage changes.
Can changing measurement units affect the importance of an effect in regression analysis?
-No, changing measurement units does not alter the underlying importance or effect of a variable in regression analysis.
What is meant by goodness of fit in the context of regression analysis?
-Goodness of fit refers to how well the regression model explains the variability of the dependent variable, which remains unaffected by changes in measurement units.
In the upcoming lab, what practical applications will be explored?
-The lab will involve analyzing a dataset related to birth weight and smoking behavior, illustrating how to apply scaling changes to various variables.
Why is it important to understand the implications of scaling and transforming variables?
-Understanding these implications is crucial for correctly interpreting regression results and ensuring accurate statistical inference.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
5.0 / 5 (0 votes)