Intro to wave superposition

Summary

This video explores wave superposition, also known as interference, where overlapping waves create combined effects. It explains how waves add algebraically when they meet, resulting in constructive or destructive interference based on their phase relationship. The video uses interactive simulations to demonstrate these concepts, showing how different waves interact and the mathematical relationships governing their interference patterns.

Takeaways

• 🌊 The concept of wave superposition refers to the overlapping of two waves, which can also be called interference.
• 📐 When two waves meet, their effects add up algebraically, resulting in the combined height of the waves.
• 🔄 If two pulses are identical, their heights add up when they meet; if they differ, their combined height is the sum of their individual heights.
• 🔄 Negative pulses can result in a net effect of zero when they align perfectly, demonstrating destructive interference.
• ⏱ The timing of the wave's movement is crucial as it determines when interference occurs.
• 🌐 Different shaped pulses can interfere, resulting in a pattern that is the sum of the overlapping patterns at any given moment.
• 🌉 Standing waves are a special case of interference where waves travel in opposite directions and create a stationary pattern.
• 🔗 The resultant wave from two interfering waves is the algebraic sum of the two individual waves.
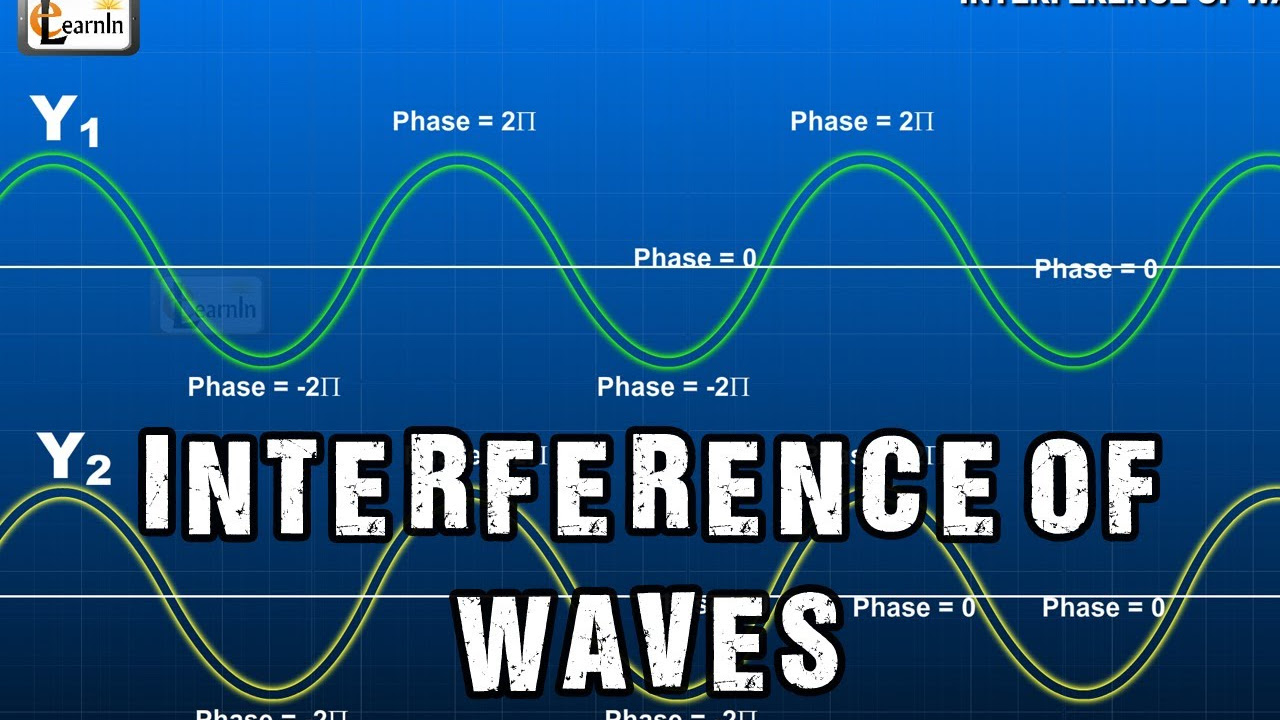
• 📉 The phase difference between two waves is critical in determining whether the interference is constructive or destructive.
• 🔄 Constructive interference occurs when the phase difference is a multiple of 2π, while destructive interference happens when the phase difference is an odd multiple of π.
• 📚 The relationship between phase difference and path difference is given by the equation Δφ = 2π/λ * Δr, where Δφ is the phase difference, Δr is the path difference, and λ is the wavelength.

Q & A

What is meant by 'superposition' in the context of waves?

Superposition refers to the overlapping of two or more waves in position and time. When this happens, the resulting wave is the algebraic addition of the individual effects of the waves.

What are the two types of interference that occur during superposition?

The two types of interference are constructive interference, where the waves combine to create a larger amplitude, and destructive interference, where the waves cancel each other out.

What happens when two identical waves meet during constructive interference?

When two identical waves meet during constructive interference, their amplitudes add together, resulting in a wave with a combined height equal to the sum of their individual heights.

How does destructive interference occur between two waves?

Destructive interference occurs when two waves meet, and one wave has a positive amplitude while the other has an equal negative amplitude. This causes their effects to cancel each other out, resulting in a net amplitude of zero at that instant.

What is a standing wave, and how is it formed?

A standing wave is a type of wave that appears to be stationary, formed by the interference of two waves traveling in opposite directions. In a standing wave, certain points (nodes) remain still while others (antinodes) oscillate with maximum amplitude.

What is the significance of phase difference in wave superposition?

Phase difference refers to the offset between the phases of two waves. It plays a crucial role in determining the type of interference. A phase difference of zero results in constructive interference, while a phase difference of 180° (or π radians) results in destructive interference.

What is the general expression for the superposition of two waves with a phase difference?

The general expression for the superposition of two waves with a phase difference is given by the equation: 2A * cos(ϕ/2) * sin(Kx - ωt + ϕ/2), where ϕ is the phase difference, K is the wave number, and ω is the angular frequency.

How does the phase difference affect the resultant wave in a simulation of superposition?

In the simulation, when two waves have a phase difference of zero, they interfere constructively, doubling the amplitude. When they have a phase difference of 180°, they interfere destructively, canceling each other out.

What are the conditions for constructive interference in terms of phase and path difference?

Constructive interference occurs when the phase difference between two waves is zero or when the path difference is an integer multiple of the wavelength (mλ, where m is an integer).

What are the conditions for destructive interference in terms of phase and path difference?

Destructive interference occurs when the phase difference is 180° (or π radians) or when the path difference is an odd multiple of half the wavelength ((m + 1/2)λ).

Outlines

00:00

🌊 Wave Superposition and Interference Basics

This paragraph introduces the concept of wave superposition, which is the overlapping of two or more waves resulting in a new wave pattern. The term 'superposition' is used when waves overlap in position and time, and this phenomenon is also known as interference. The video demonstrates what happens when two pulses meet and overlap, resulting in the algebraic addition of their individual heights. The concept of constructive and destructive interference is introduced, where constructive interference occurs when the combined height of overlapping waves is the sum of their individual heights, and destructive interference occurs when the waves cancel each other out, resulting in a net effect of zero. The video also touches on the idea that energy is not destroyed in destructive interference, but rather the effects cancel out. The simulation of wave interference is suggested as a way to explore these concepts further.

05:00

🌊 Exploring Wave Superposition with Phase Differences

The second paragraph delves deeper into wave superposition, focusing on the role of phase differences between waves. It explains that when two waves with the same amplitude and wavelength have a phase difference, their superposition results in a new wave pattern that is the algebraic sum of the two original waves. The video uses a mathematical identity to simplify the expression for the resulting wave when there is a phase difference. The identity used is 2 * cos((a - b)/2) * sin((a + b)/2), where 'a' and 'b' represent the phase angles of the two waves. The video also discusses how to use an interactive physics simulation to explore wave interference and how changing the phase difference affects the resulting wave pattern. The concept of standing waves is briefly mentioned as a special case of wave interference.

10:01

🌊 Constructive and Destructive Interference Explained

In this paragraph, the video script explains the conditions for constructive and destructive interference in more detail. Constructive interference occurs when the phase difference between two waves is an integer multiple of 2π (or 360 degrees), resulting in the peaks and valleys of the waves aligning perfectly, thus doubling the amplitude. Conversely, destructive interference happens when the phase difference is an odd multiple of π (or 180 degrees), leading to the peaks of one wave aligning with the valleys of the other, effectively canceling each other out. The video uses a simulation to visually demonstrate these concepts, showing how changing the initial conditions of the waves can result in either constructive or destructive interference. The relationship between phase difference and path difference is also discussed, highlighting the importance of understanding these concepts for studying wave behavior.

15:05

🌊 General Conditions for Constructive and Destructive Interference

The final paragraph summarizes the general conditions for constructive and destructive interference. It reiterates that constructive interference occurs when the path difference between two waves is an integer multiple of the wavelength (Mλ, where M is an integer), and destructive interference occurs when the path difference is an odd multiple of half a wavelength ((m + 1/2)λ). The video script emphasizes the importance of these equations for understanding wave interference and suggests that they will be practiced in class. The paragraph concludes by reinforcing the significance of these concepts and their application in solving wave-related problems.

Keywords

💡Superposition

Superposition is a fundamental concept in wave physics referring to the phenomenon where two or more waves overlap in space and time. In the video, it is explained that when waves superpose, their effects are combined through algebraic addition. This concept is crucial for understanding wave interference, as it shows how waves can either constructively or destructively interfere depending on their phase relationship. For instance, when two identical pulses meet, they add up to create a pulse with double the amplitude, illustrating constructive superposition.

💡Interference

Interference is the process that occurs when two waves superpose, resulting in a new wave pattern. The video explains that interference can be constructive, where waves add up to create a wave with greater amplitude, or destructive, where they cancel each other out. This concept is central to the video's theme, as it demonstrates how the interaction of waves can lead to various outcomes, such as the formation of standing waves.

💡Destructive Interference

Destructive interference happens when two waves with equal amplitudes meet out of phase, causing their amplitudes to cancel each other out. The video uses the example of a wave with a positive amplitude and another with a negative amplitude (3 and -3) to illustrate how their superposition results in a net effect of zero, which is a clear case of destructive interference.

💡Constructive Interference

Constructive interference is the opposite of destructive interference, where two waves with the same phase add up to form a wave with a larger amplitude. The video mentions that when two pulses of the same height meet, their heights combine to form a pulse with a height that is the sum of the individual heights, demonstrating constructive interference.

💡Phase Difference

Phase difference refers to the difference in phase between two waves. In the video, it is used to explain how the relative timing of wave cycles affects the interference pattern. A phase difference of zero degrees (or zero radians) results in constructive interference, while a phase difference of 180 degrees (or pi radians) results in destructive interference. The video uses this concept to discuss how changing the phase of one wave relative to another can shift the interference from constructive to destructive.

💡Wavelength

Wavelength is the physical length of one wave cycle and is used in the video to discuss the conditions for constructive and destructive interference. The video explains that if the path difference between two waves is an integer multiple of the wavelength, constructive interference occurs. This is a key concept in understanding how waves can synchronize and create standing waves.

💡Standing Wave

A standing wave is a wave pattern that appears to remain in a constant position, formed by the interference of two waves traveling in opposite directions. The video introduces this concept by showing a simulation where two waves, one traveling to the right and the other to the left, create a standing wave pattern. This is an important concept as it illustrates a special case of wave interference.

💡Path Difference

Path difference is the physical distance by which the phase of one wave leads or lags behind another. The video explains that the path difference is directly related to the phase difference and can be used to predict whether waves will interfere constructively or destructively. It is mentioned that if the path difference corresponds to an integer multiple of the wavelength, constructive interference occurs.

💡Wave Speed

Wave speed is the rate at which a wave propagates through a medium. Although not explicitly mentioned as 'wave speed' in the video, it is implied in the discussion of how waves travel and interfere over time. The video script mentions that waves have a speed of travel, which is essential for understanding how they can meet and interfere at certain points.

💡Trigonometric Identity

The video uses a trigonometric identity to simplify the mathematical expression for the superposition of two waves with a phase difference. Specifically, the identity sin(A) + sin(B) = 2cos((A-B)/2)sin((A+B)/2) is applied to show how two waves can combine to form a new wave pattern. This identity is crucial for understanding the algebraic addition of wave effects.

Highlights

Introduction to wave superposition and interference.

Definition of superposition as overlapping waves.

Explanation of constructive and destructive interference.

Demonstration of wave interaction through a simulation.

How waves of different heights combine during superposition.

Impact of negative waves on superposition and interference.

Importance of time in wave motion and interference.

Different shapes of waves and their interference patterns.

Interactive physics simulations for wave interference.

Standing wave formation and its characteristics.

General formula for wave superposition involving phase differences.

Use of trigonometric identity in wave superposition calculations.

Derivation of the resultant wave equation from phase differences.

Visual representation of constructive interference in simulations.

Visual representation of destructive interference in simulations.

Explanation of phase difference and its impact on wave interference.

Conversion between phase difference and path difference using wave number.

Conditions for constructive interference in terms of phase and path differences.

Conditions for destructive interference and their mathematical representation.

Transcripts

today in this video we're going to start

chapter 17 oops chapter

17 that talks about

superposition of

waves now the word superposition is just

fancy

for for uh in our case for

overlapping what if we overlap two waves

let me see is it this one no

there you go super position it's also

called interference when two waves or

two pulses overlap in position and time

we call it we call that superp position

or interference and let's run this thing

you see we have one pulse traveling to

the right one pulse traveling to the

left and we'll see what happens when

they meet when they meet well they

overlap and the effect is well just the

algebraic addition of their individual

effects right that's all that's superp

position if I let them run we'll see

them

interfere I can we don't we don't need

to show the individual this is just the

the Rope the string what it feels what

it does is well the it follows the

addition of the individual contributions

now

now in this case two pulses were

different let's if we make the two

pulses the same like three and

three in height look when they

meet their height combined height is six

right if one of them is one and the

other one is three then the combined

height is four that's all now what if

one of the pulses is

negative well let's in this case three

and minus three well 3 + -3 is zero and

sure enough for an instant when the two

pulses align perfectly the net effect is

zero now the energy is still there we

you didn't destroy the energy this is

still there all the work

right so remember this has to do with

time as well the wave moves has a speed

travel so at one point they will they

will interfere and nothing nothing will

happen nothing will appear to to be

shown right this this type of

interference when everything cancels we

call it destructive interference in the

other in the other section in the other

hand this is constructive

interference of course the interference

can happen uh between pulses of any shap

shape like this one for instance this is

like an M the other one is like a ramp

and when they

meet you always get the

resultant

of the patterns that are that are

overlapping at that instant of time yeah

this is this is um this is a nice

simulation you can play with this with

this

um with this

patterns if you want let me see if I can

move this yeah here it's called o

physics interactive physics simulations

go to waves go to wave pulse

interference super position number two

and then you can have some fun with

this you can also make not only pulses

but waves interfere and if and if we do

this let's play this you see well in

this case we have one wave traveling to

the right one wave traveling to the left

this is a peculiar um type of wave that

we will study in this chapter it's

called a standing wave but is not the

only possibility let's let's go in

opposite directions no they're in the

same direction but there's the same

wave where is the other

one

yeah let me see one is like

this um show red

I don't know where the red one is oh

there you go same direction so I'm

sending the red one and the blue one and

I get the purple one so you play with

different wavelengths and then you get

different results of

course

um you

see what you get is the net effect of

adding the two

waves right like this purple is the red

and the blue that's all in this case

they're traveling in the same direction

if I make them travel in opposite

directions well this is what you're

going to get at at all times what you

get it's at this point is is the red

plus the blue the red plus the blue the

red plus the blue is algebraic so it

could be positive or could be

negative all

right now I'm I'm interested in this

type of interference this is the first

special case of interference that we

will um we will um study okay in general

interference you have the red function f

of XT and then you have the green

function G of XT so the blue function is

just the red plus the green that's it

you add one wave plus the other one you

get the blue wave that that simple let's

do

it so

let's say we have function

one which is one wave just a normal

traveling

wave okay and then we have the other one

which is that is going to be the same

wave meaning same amplitude same

wavelength same X same frequency same

Omega but to this one I'm going to add a

different face so the only difference

between these two is that the face is

not this same okay this is the first

scenario of superposition right if the

face are not the same so the total wave

is just going to be one wave plus the

other so a

sin KX - Omega t + a sin KX - Omega t +

5 and that's it that's a superimposed

wave now I'm going to use a little

identity

s of a + S of B is 2 cosine of a minus B

/

2 s of a + b / 2 okay I'm going to use

that identity in which this is a and

this is

B and that's going to give

us so I'm going to I'm going to factor

the a of course then is going to be sign

so this all this is a so oh

actually actually so s of a plus s of b

i factored the a so we're going to have

2 cosine a minus B so

KX - Omega t - KX - - plus Omega t - 5

and all this over two and then

s of a + b KX - Omega t+ KX - Omega t +

5 and all that's over two and then what

happens here is the KX cancel the KX

Omega T cancels Omega T and then what we

get is a 2 cosine of - 5 / 2 and on the

other side we get S of KX KX that's

2K 2 KX - Omega t - Omega t - 2 Omega t

+ 5 and all of this over

two right that's so what we get is 2 a I

want to put the two outside

cosine - 5/ two and then

sign the two the two cancel this two and

this two cancel and this becomes so KX -

Omega t + 5 / 2 okay and this is the

expression we were looking

for oops that's the total that's the

wave right that's the wave you get when

the only difference is the phase

difference meaning phase difference in

this case we call it five and that's

what the book calls it I will call it

Delta

F but if you read the book it's going to

say just fine and that's the reason is

because they are assuming that the phase

initially is zero okay but and it's true

one of the fa here the phase of this one

was zero so phase or Delta phase means

phase

difference all

right and uh it's just it just I will I

will explain this more in class what the

phase difference means in terms of let's

say how two waves are generated but when

you have this is a very general

expression and and um the way it looks

like is in the simulation here if I play

it look I'm sending the red the Red Wave

and I'm sending the Green Wave at this

point they are in face you see Peak with

Peak valid with valid Peak with Peak

valid with valid so when they add at all

times they are in constructive

interference because what the peak Peak

with Peak get you get twice the peak

valy with Valley you get twice the

valley

right that the equation tells us that

here when the face difference is zero

cosine of 0 is 1 and you get twice the

original wave you see how this is the

original wave the phase difference is

zero you get just twice the original

wave here you see it's the same thing

and that's what we are seeing when the

when the when the face is is zero you

get twice the wave twice as loud or

twice as intense but if you have a

difference and I'm going to put Express

the difference with

this okay yeah you see how um look at

the r red and green what I'm saying is

at the

beginning the the red and the green let

me let me do this let me do this better

okay there you go here look where the

green where is the initial conditions of

the green

and the initial conditions of the red

here they're the same so the face of the

red at the beginning which is Rel it's

expressed by this gray block the face of

the Red Wave and the face of the Green

Wave are exactly the same so you have a

pH of zero if I change the

face you see now the faces are different

this red red one is here the green one

is somewhere

there so the the total wave at all times

is almost non-existent because you are

almost always in a in a position of

destructive interference look Peak with

Valley Valley with Peak Peak with Valley

so they destroy each other and at this

point you are completely out of phase

the phase difference here is 180° or

actually pi and if we look at the

equation what would happen if you put 5

equal to to 180 well 180 over 2 is 90

cosine of 90 is zero you don't get a

wave right you get destructive

interference now let's take a look when

you have a

wave that's ugly let's do it again when

you have a

wave right um

here with

this I'll grabe this one when they are

in Phase well they look like this they

have zero degrees or zero radians in

facee difference so they are in

constructive interference when you're

completely out of phase then you have

Peak with Valley so the the phase

difference Delta fi when the Delta when

the Delta F when the phase difference is

equal to 2 pi 360 de face

difference well the the the distance or

the the the difference in

path between this point and this point

which is called Delta R it's equal to

Lambda that's the path difference that

means one wavelength is ahead of the

other one by one wavelength or the one

wavelength is behind the other one by

one wavelength and you can divide these

two equations and what you get is that

the path difference the phase difference

over the path difference is 2 pi/ Lambda

and if you remember that's the wave

number so this is a nice equation to

have in your equation sheet because

allows you to convert from phase

difference to path difference and we're

going to practice this also in class

lastly let's consider these two waves

here we know they are completely in

Phase so constructive interference here

destructive interference let's consider

when they are in constructive

interference when they are in

constructive interference what we can

say

is conditions for

constructive well what about we need the

phase difference to be zero right or the

path difference to be zero MERS when

there is no path difference or not or no

phase difference we know we have

constructive interference Peak with Peak

value with value but what happens if one

wave is ahead head of the other one by a

full wavelength like this one you see

now what you get is you get this peak

interfering with this peak and this peak

interfering with with the with the next

one so in this case the path difference

the phas difference

is my God the phas difference is 2

pi and the path difference is one

wavelength and you still get

constructive interference

what if you are two wavelengths

ahead I want to put them down here what

if you are two wavelengths

ahead right this peak instead of

interfering with this peak is

interfering with that one so you're two

wavelengths ahead so now you're two

wavelengths ahead whatever 4 PI right

and then if you were three lambdas 6 Pi

or four lambdas you will always get

constructive interference in actually

the main the in general if the path

difference is M Lambda where M can be

any integer 0 1 2 Etc you get

constructive

interference for destructive

interference let's take a look here is

constructive but here is the structive

you see Peak with Valley valy with Peak

so the conditions for the structive

interference is

R you get

destructive if the

phas or the

path well when the phase is

pi right or the path is Lambda over 2

you get destructive interference but the

same will happen with three Lambda over

2 right there will be one wavelength and

a half ahead like this and you will get

the structure interference the same will

happen with 5 Lambda / 2 7 Lambda / 2 so

in general you get destructive

interference when the path difference is

m + 12 of Lambda again m is 0 1 2 3 Etc

so these two equations are very

important

um they are General General scenarios of

the equation we first derived with the

cosine 5 / 2 and these two equations are

important we're going to do problems

involving these two in class