Peluang ( probabilitas ) - peluang statistika materi dan contoh soal
Summary
TLDRThis video tutorial provides a comprehensive introduction to the concept of probability, explaining essential terms like sample space, events, and complementary events. The presenter covers various probability calculations with clear examples, such as the probability of drawing even-numbered cards from a deck and the chances of rolling a specific number on a die. Topics such as independent, dependent, and mutually exclusive events are explored, along with conditional probability. The tutorial is aimed at helping viewers understand and apply probability theory through engaging examples and easy-to-follow steps.
Takeaways
- 😀 Probability is a mathematical concept used to measure the likelihood of an event occurring, and is also known as 'peluang' or 'probabilitas' in Indonesian.
- 😀 The sample space (*ruang sampel*) represents all possible outcomes of an experiment, and sample points (*titik sampel*) are the individual outcomes within that space.
- 😀 The formula for calculating the probability of an event A is: P(A) = n(A) / n(S), where n(A) is the number of favorable outcomes and n(S) is the total number of outcomes.
- 😀 Complementary events are events that cannot occur simultaneously, and their probability is calculated as P(A') = 1 - P(A), where P(A') is the complement of event A.
- 😀 Expected frequency is the predicted number of times an event will occur in repeated trials, calculated as E(A) = P(A) × n, where n is the number of trials.
- 😀 Two events are independent if the occurrence of one does not affect the other. The probability of both events A and B occurring is P(A ∩ B) = P(A) × P(B).
- 😀 Dependent events occur when the outcome of one event affects the outcome of another, and the conditional probability is calculated as P(B|A) = P(A ∩ B) / P(A).
- 😀 Mutually exclusive events are events that cannot occur at the same time. The probability of either event A or B occurring is P(A ∪ B) = P(A) + P(B).
- 😀 Real-life examples of probability calculations include drawing cards from a deck or rolling dice, where you calculate the likelihood of specific outcomes (e.g., even or prime numbers).
- 😀 Probability can be used in real-world applications, such as determining the likelihood of an employee being chosen based on conditions like gender or employment status.
Q & A
What is the definition of probability as explained in the video?
-Probability, also known as chance or likelihood, is a mathematical concept used to determine the possibility of an event occurring. It is calculated as the ratio of favorable outcomes to total possible outcomes in a given experiment.
What are the key terms used in probability theory as discussed in the video?
-The key terms include 'ruang sampel' (sample space), which refers to all possible outcomes, 'titik sampel' (sample point), which is an individual outcome within the sample space, and 'kejadian A' (event A), which is a subset of the sample space.
What is the formula for calculating the probability of an event?
-The probability of an event A is calculated using the formula: P(A) = n(A) / n(S), where n(A) is the number of favorable outcomes for event A, and n(S) is the total number of possible outcomes (the size of the sample space).
How did the example of drawing an even-numbered card from a deck illustrate probability?
-In the example, a card is drawn from a deck of 52 cards. The probability of drawing an even-numbered card was calculated by identifying that there are 20 even-numbered cards (2, 4, 6, 8, 10, each in four suits). The probability is therefore 20/52, which simplifies to 5/13.
What is the concept of expected frequency, and how is it calculated?
-Expected frequency (frekuensi harapan) refers to the anticipated number of times an event occurs in a given number of trials. It is calculated by multiplying the probability of the event by the number of trials, i.e., E(A) = P(A) × F.
Can you explain complementary probability as discussed in the video?
-Complementary probability refers to the likelihood of the opposite event occurring. If P(A) is the probability of event A, then the probability of event A not occurring is given by P(A') = 1 - P(A). An example in the video shows how to calculate the probability of not rolling a prime number on a die.
What are mutually exclusive events, and how are they calculated?
-Mutually exclusive events are events that cannot happen at the same time. The probability of either event A or event B occurring is calculated using the formula: P(A ∪ B) = P(A) + P(B) - P(A ∩ B), where P(A ∩ B) is the probability of both events occurring simultaneously.
What does it mean for two events to be independent, and how is their probability calculated?
-Two events are independent if the occurrence of one does not affect the occurrence of the other. The probability of both independent events A and B happening is calculated by multiplying their individual probabilities: P(A ∩ B) = P(A) × P(B).
How is conditional probability different from other types of probability?
-Conditional probability refers to the probability of event A occurring given that event B has already occurred. It is calculated using the formula: P(A | B) = P(A ∩ B) / P(B), which takes into account the relationship between the two events.
How does the example with dice help explain the concept of conditional probability?
-In the dice example, the conditional probability of rolling an odd number, given that the number is divisible by 3, is calculated by first determining the outcomes that satisfy the condition (3 and 6), then finding the overlap (the number 3), and applying the conditional probability formula to get the result.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Peluang, Peluang kejadian, frekuensi harapan, peluang komplemen

STATISTIKA | KONSEP DASAR PROBABILITAS

Probabilitas 01 Pengenalan Probabilitas Dasar | Belajar Probabilitas

PROBABILIDADE | MATEMÁTICA | QUER QUE DESENHE
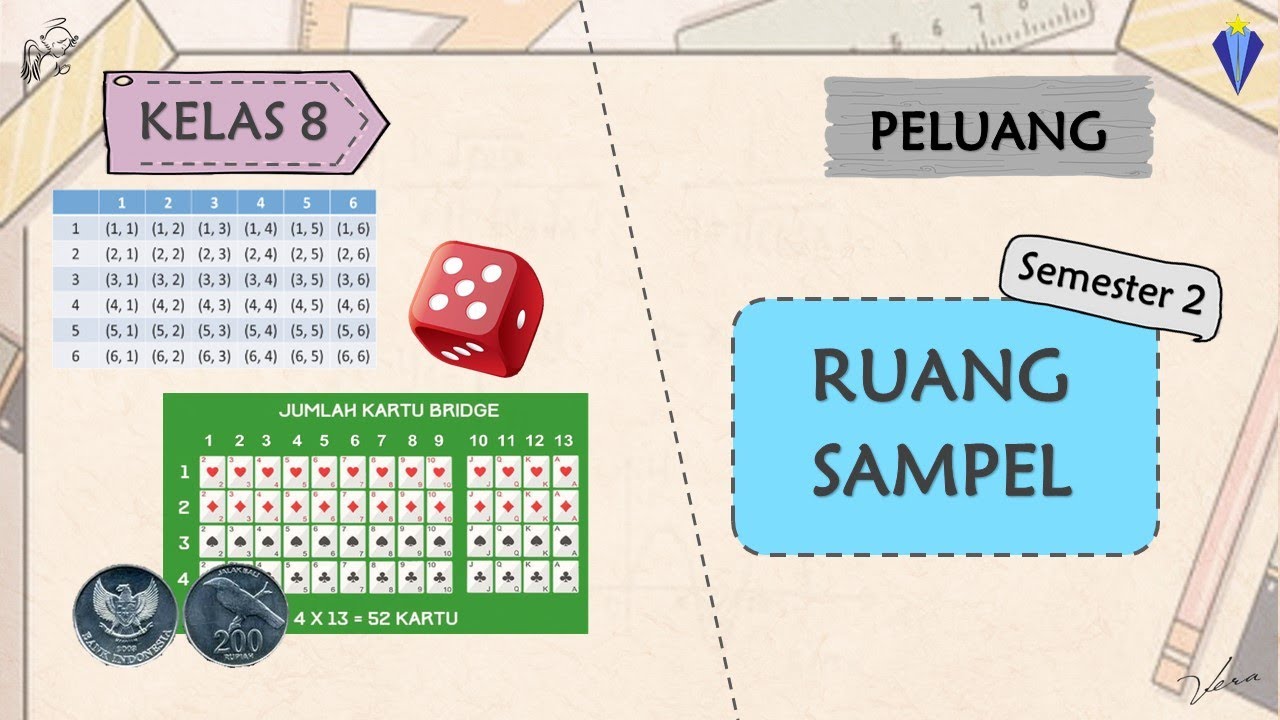
1. RUANG SAMPEL - PELUANG - KELAS 8 SMP

Peluang [Part 1] - Ruang Sampel dan Titik Sampel
5.0 / 5 (0 votes)