Nodal Analysis
Summary
TLDRThis video tutorial provides a comprehensive introduction to nodal analysis in electrical circuits, contrasting it with mesh analysis. It covers the key steps in performing nodal analysis, such as identifying nodes, assigning voltages, developing KCL equations, and solving for node voltages. The tutorial also includes an example problem to demonstrate the process, highlighting the use of Kirchhoff's Current Law (KCL) to balance currents at non-reference nodes. The session emphasizes the applicability of nodal analysis to both planar and non-planar networks and provides a clear method for solving for voltages and currents efficiently.
Takeaways
- 😀 Nodal analysis is based on Kirchhoff's Current Law (KCL), while mesh analysis is based on Kirchhoff's Voltage Law (KVL).
- 😀 A node is defined as the common point where two or more elements are connected, with a simple node having two connections and a principal node having more than two.
- 😀 Current division occurs at principal nodes in nodal analysis, and KCL equations are developed for non-reference nodes.
- 😀 The steps to perform nodal analysis include identifying the number of nodes, assigning node voltages, developing KCL equations for non-reference nodes, and solving the equations to find the node voltages.
- 😀 In nodal analysis, one node is chosen as the reference node, and its voltage is set to zero. The other nodes are treated as non-reference nodes.
- 😀 Nodal analysis is applicable for both planar and non-planar networks, unlike mesh analysis which is only applicable for planar networks.
- 😀 The number of KCL equations required in nodal analysis is equal to the number of nodes (n) minus 1 (i.e., n-1).
- 😀 When assigning voltages, the reference node is typically chosen as the node where most branches are connected or the bottom node in the diagram.
- 😀 In the example, current sources are accounted for directly by using their given values, while resistive branches require applying Ohm's Law in the KCL equations.
- 😀 KCL equations are formulated by summing the currents leaving a node and setting the sum equal to zero, following the sign conventions of current direction.
- 😀 In the example problem, the node voltage VX is determined by solving the KCL equation, leading to the calculation of the current (I) as 2 amperes.
Q & A
What is the difference between mesh analysis and nodal analysis?
-Mesh analysis is based on Kirchhoff's Voltage Law (KVL), where we develop equations based on the voltages around loops or meshes in a circuit. Nodal analysis, on the other hand, is based on Kirchhoff's Current Law (KCL), where we develop equations for the currents at the nodes or junctions where multiple elements are connected.
What is a node in electrical circuits, and what is the difference between a simple node and a principal node?
-A node is a common point where two or more elements are connected in a circuit. A simple node is where only two elements are connected, while a principal node is where more than two elements are connected. Current division occurs at a principal node, while it does not occur at a simple node.
What is the first step in performing nodal analysis?
-The first step in nodal analysis is to identify the total number of nodes in the circuit. These nodes are the points where multiple elements are connected, and they can be either simple or principal nodes.
How is the reference node chosen in nodal analysis?
-The reference node is chosen as the node where the potential is defined as zero volts. It is typically the node where the most branches are connected, but it is commonly taken as the bottom node for simplicity.
What is the significance of the reference node in nodal analysis?
-The reference node is crucial because it sets the potential at zero volts, providing a common ground for all other node voltages in the circuit. All other nodes are referenced relative to this node.
What does the KCL equation represent in nodal analysis?
-The KCL equation represents the sum of currents at a node. According to Kirchhoff's Current Law, the sum of currents entering a node is equal to the sum of currents leaving the node. In nodal analysis, the equation is developed for each non-reference node.
What is the formula for determining the number of equations needed in nodal analysis?
-The formula for determining the number of equations required is E = N - 1, where E is the number of equations and N is the total number of nodes. The reference node is not included in the equation count.
How is the current for each branch defined when writing the KCL equation?
-When writing the KCL equation, the current for each branch is defined based on the potential difference between the node voltage and the voltage at the other end of the branch. The direction of the current is assigned based on the assumed polarity of the voltages, and currents leaving the node are considered positive.
Why is the current direction important when writing the KCL equation?
-The direction of the current is important because it determines whether the current contributes positively or negatively to the KCL equation. In general, currents leaving the node are considered positive, while currents entering the node are considered negative.
How can the value of a node voltage be calculated in nodal analysis?
-The value of a node voltage can be calculated by solving the KCL equations for the non-reference nodes. Once the KCL equations are set up, the node voltages can be determined by solving the system of equations using methods like substitution, matrix techniques, or numerical solvers.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Kirchhoff's Voltage Law (KVL) - How to Solve Complicated Circuits | Basic Circuits | Electronics

Video Pembelajaran Modul 2 & 3 Praktikum Rangkaian Listrik 2024/2025 (DK)

Rangkaian Listrik - Analisis Mesh (Genap 2019/2020)
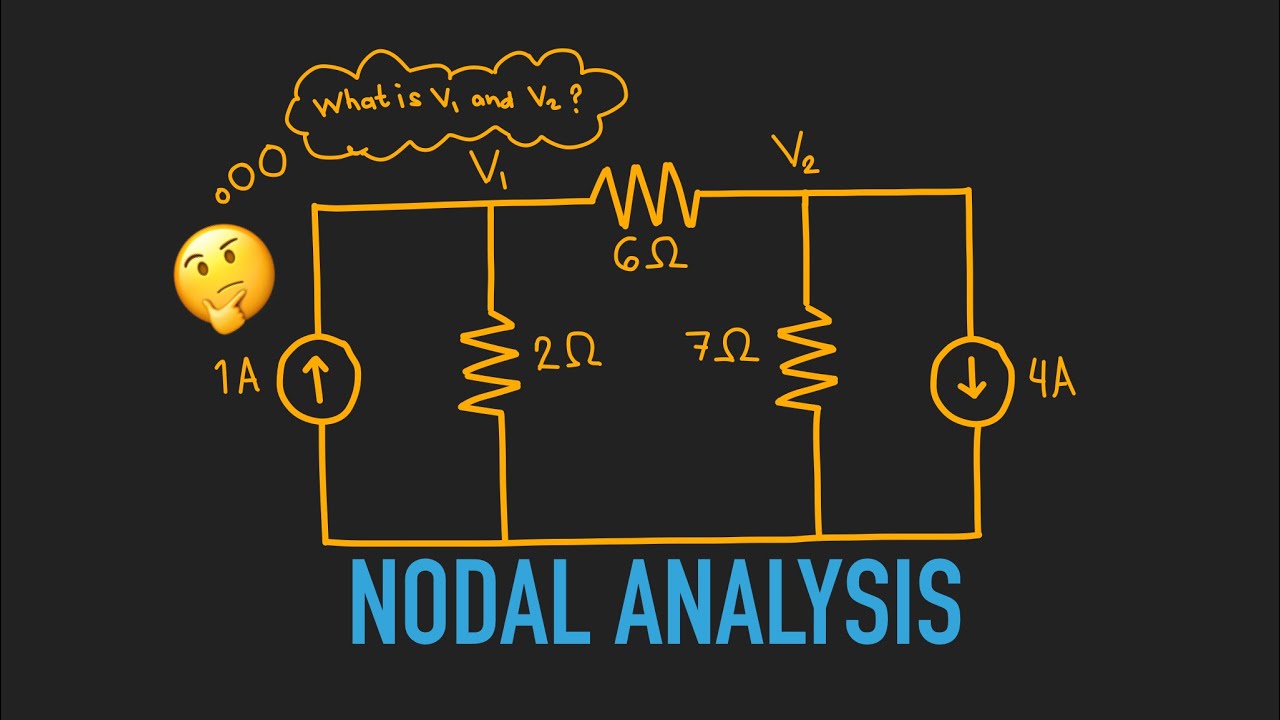
Nodal Analysis EP.16 (Tagalog/English Electronics)

Thevenin Theorem problems in Hindi [ Problem 1 ]

Series & Parallel Circuits EXPLAINED with Kirchhoff's Circuit Laws // HSC Physics
5.0 / 5 (0 votes)