TANGENTS AND SECANTS OF A CIRCLE || GRADE 10 MATHEMATICS Q2
Summary
TLDRThis video lesson covers the concepts of tangents and secants of a circle, explaining their properties, key theorems, and the angles formed by their intersections. It outlines how tangents touch a circle at one point, how they are perpendicular to the radius, and provides theorems for various geometric relationships involving tangents and secants. The video also explores common tangents, secants, and the different angle measurements formed by these lines. Through practical examples and visual illustrations, the video clarifies these important geometric principles for learners studying circle geometry.
Takeaways
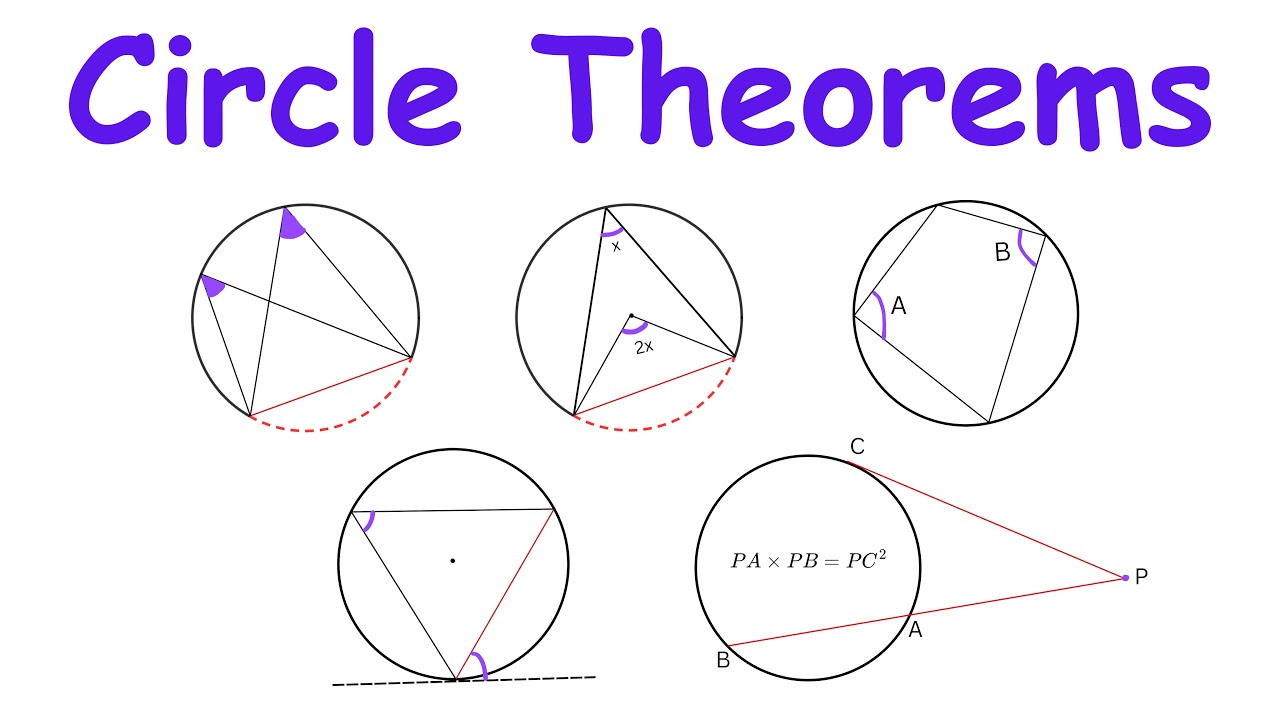
- 😀 A tangent line to a circle touches the circle at exactly one point, known as the point of tangency.
- 😀 There is only one tangent line that can be drawn at a given point on a circle.
- 😀 The first theorem states that if a line is tangent to a circle, it is perpendicular to the radius drawn to the point of tangency.
- 😀 The second theorem says that if a line is perpendicular to the radius at a point on the circle, then it is tangent to the circle.
- 😀 The third theorem states that two segments from the same exterior point that are tangent to a circle are congruent.
- 😀 A common tangent is a line tangent to two circles in the same plane, which can either be internal or external.
- 😀 Internal tangents intersect the segment joining the centers of two circles, while external tangents do not.
- 😀 A secant is a line that intersects a circle at exactly two points, whereas a tangent intersects a circle at exactly one point.
- 😀 When two secants intersect outside a circle, the angle formed is half the positive difference between the measures of the intercepted arcs.
- 😀 If a secant and a tangent intersect outside the circle, the angle formed is half the positive difference of the intercepted arcs.
- 😀 When two secants intersect inside a circle, the angle formed is half the sum of the intercepted arcs and their vertical angle.
Q & A
What is a tangent line to a circle?
-A tangent line to a circle is a line that is coplanar with the circle and intersects it at exactly one point. This point of intersection is called the point of tangency.
What is the postulate regarding tangent lines to a circle?
-The postulate states that for any given point on a circle, exactly one line can be drawn that is tangent to the circle at that point.
What does the first theorem about tangents state?
-The first theorem states that if a line is tangent to a circle, it is perpendicular to the radius drawn to the point of tangency.
Explain the second theorem regarding perpendicular lines to a radius.
-The second theorem states that if a line is perpendicular to a radius of a circle at its endpoint on the circle, then the line is tangent to the circle.
What is the third theorem about tangent segments from the same exterior point?
-The third theorem states that if two segments from the same exterior point are tangent to a circle, then these two segments are congruent.
What is a common tangent?
-A common tangent is a line that is tangent to two circles in the same plane. There are common internal tangents (which intersect the segment joining the centers of the two circles) and common external tangents (which do not intersect the segment joining the centers).
What is a secant line?
-A secant line is a line that intersects a circle at exactly two points.
What is the angle formed by two secants intersecting outside the circle?
-If two secants intersect outside the circle, the angle formed is half the positive difference of the measures of the intercepted arcs.
What happens when a secant and a tangent intersect in the exterior of a circle?
-When a secant and a tangent intersect in the exterior of a circle, the angle formed is half the positive difference of the measures of the intercepted arcs.
What is the formula for calculating angles formed by secants intersecting in the interior of a circle?
-If two secants intersect in the interior of a circle, the angle formed is half the sum of the measures of the intercepted arcs and their vertical angles.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade Now5.0 / 5 (0 votes)