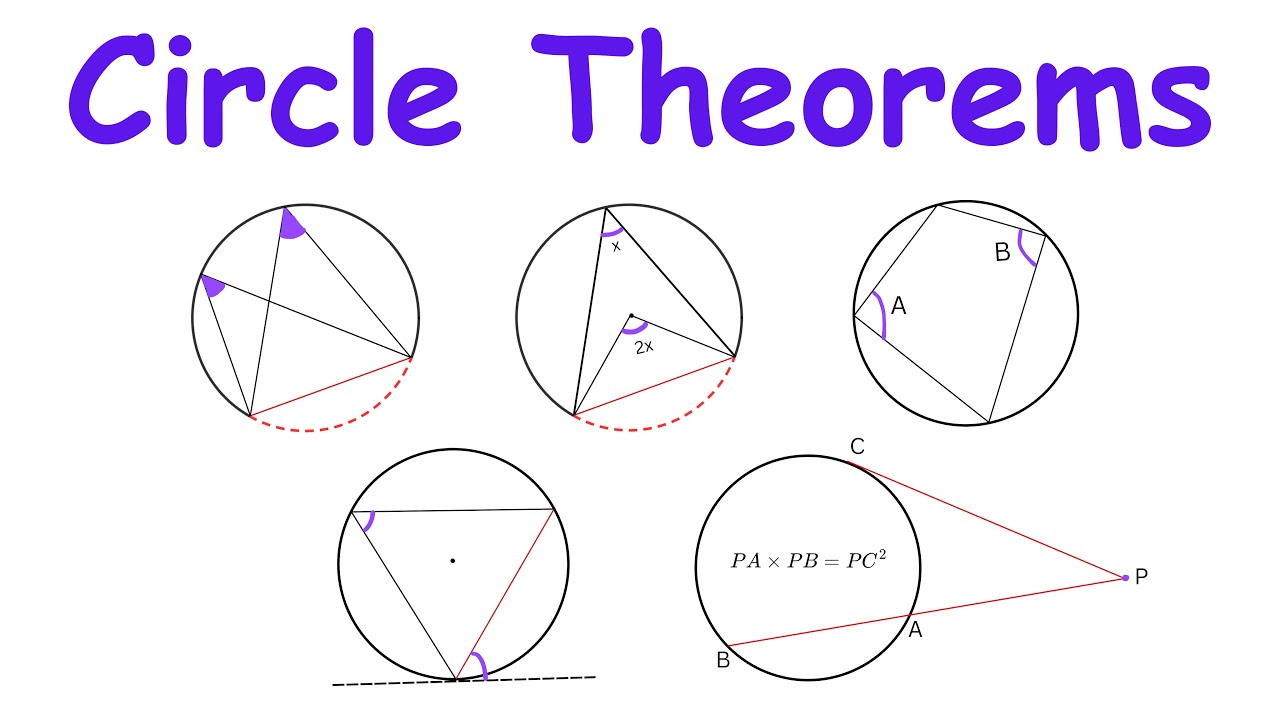
THEOREMS ON ANGLES FORMED BY TANGENTS AND SECANTS || GRADE 10 MATHEMATICS Q2
Summary
TLDRThis video lesson covers key theorems on angles formed by tangents and secants in circles. It explains various scenarios such as when two secants intersect outside or inside a circle, or when a tangent and secant intersect outside a circle. The lesson provides step-by-step examples demonstrating how to calculate angle measures based on intercepted arcs. Several practice problems help clarify the application of these theorems, with solutions provided to reinforce the concepts. The video also emphasizes important properties like supplementary angles and vertical angles in geometric contexts.
Takeaways
- 😀 Angles formed by two secants intersecting outside a circle are half the positive difference between the intercepted arcs.
- 😀 When two tangents intersect outside a circle, the angle formed is half the positive difference of the intercepted arcs.
- 😀 For two secants intersecting inside a circle, the angle formed is half the sum of the intercepted arcs.
- 😀 The angles that form a linear pair (e.g., vertical angles) are supplementary, adding up to 180°.
- 😀 Vertical angles are congruent, which means that when two angles form a vertical pair, their measures are equal.
- 😀 In problems involving algebraic expressions for arcs, the angle formed can be calculated by substituting the values into the appropriate formula.
- 😀 The formula for calculating the angle formed by two secants in the exterior of the circle involves subtracting the measures of the arcs and dividing by two.
- 😀 Similarly, for two tangents intersecting in the exterior of a circle, the angle formed is half the difference of the intercepted arcs.
- 😀 The sum of the measures of the intercepted arcs, when a secant and tangent intersect in the exterior, helps calculate the angle formed.
- 😀 Problems involving unknown variables in arcs can be solved by setting up equations, simplifying, and solving for the unknown to find the angle or arc measures.
Q & A
What is the formula for finding the angle formed by two secants intersecting outside a circle?
-The formula is: Angle = 1/2 * |(measure of intercepted arc 1) - (measure of intercepted arc 2)|.
If the measure of arc CE is 160° and the measure of arc BD is 80°, what is the measure of angle CAE?
-The measure of angle CAE is 40°. This is calculated as 1/2 * (160 - 80) = 1/2 * 80 = 40°.
What is the formula for finding the angle formed by two tangents intersecting outside a circle?
-The formula is: Angle = 1/2 * |(measure of intercepted arc 1) - (measure of intercepted arc 2)|.
If arc PQR is 220° and arc PR is 140°, what is the measure of angle PMR?
-The measure of angle PMR is 40°. This is calculated as 1/2 * (220 - 140) = 1/2 * 80 = 40°.
When two secants intersect inside a circle, how do you calculate the angle formed?
-The angle formed is calculated as 1/2 * (sum of the measures of the intercepted arcs).
If arc EB is 45° and arc CD is 49°, what is the measure of angle EFB?
-The measure of angle EFB is 47°. This is calculated as 1/2 * (45 + 49) = 1/2 * 94 = 47°.
What is the relationship between vertical angles formed by intersecting secants or tangents?
-Vertical angles are congruent, meaning they have the same measure.
If arc EB is 6x + 5 and arc CD is 4x + 15, and angle EFB is 60°, how do you find the value of x?
-You set up the equation 60 = 1/2 * [(6x + 5) + (4x + 15)], simplify it to solve for x. The value of x is 10.
How do you find the measure of angle BFD if angle EFB is 60° and angle BFD is supplementary to it?
-Since angle EFB and angle BFD are supplementary, you subtract the measure of angle EFB from 180°. Thus, angle BFD is 180° - 60° = 120°.
If a secant and a tangent intersect outside a circle, how do you calculate the angle formed by them?
-The formula is: Angle = 1/2 * |(measure of intercepted arc) - (measure of arc of the tangent)|.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade Now5.0 / 5 (0 votes)