Pearson correlation [Simply explained]

Summary

This video explains Pearson correlation, a statistical method used to measure the strength and direction of the linear relationship between two variables. It covers key concepts such as positive and negative correlations, how to calculate the Pearson correlation coefficient, and the difference between correlation and causation. The video also highlights the importance of hypothesis testing to determine statistical significance and discusses the assumptions required for accurate analysis. Ideal for those looking to understand the practical and theoretical aspects of Pearson correlation in data analysis.

Takeaways

• 😀 Pearson correlation measures the linear relationship between two variables, like age and salary.
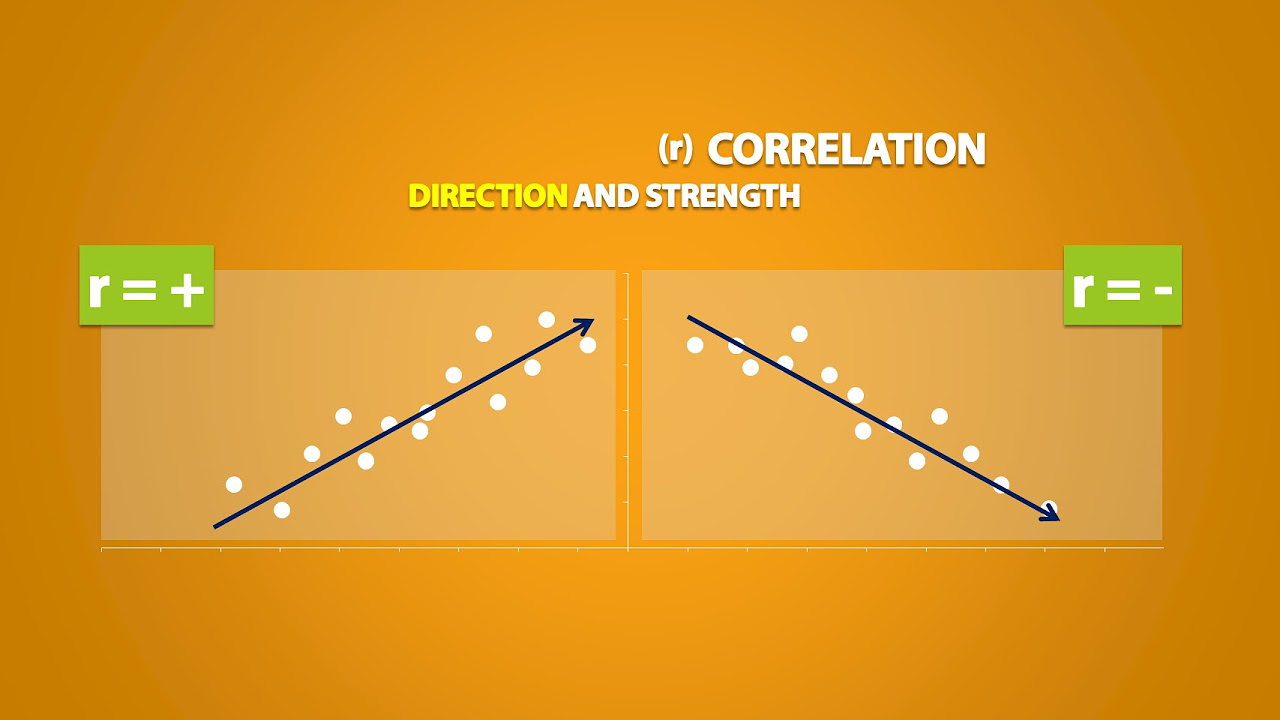
• 😀 A scatter plot visually represents the relationship between two variables, where each point represents an individual data point.
• 😀 Pearson correlation does not imply causation; just because two variables are correlated does not mean one causes the other.
• 😀 The Pearson correlation coefficient (R) ranges from -1 to 1 and indicates the strength and direction of the relationship.
• 😀 A correlation coefficient between 0 and 0.1 indicates no correlation, while a value between 0.7 and 1 indicates a very strong correlation.
• 😀 Positive correlation occurs when large values of one variable correspond with large values of another (e.g., body size and shoe size).
• 😀 Negative correlation occurs when large values of one variable correspond with small values of another (e.g., product price and sales volume).
• 😀 The Pearson correlation coefficient is calculated by subtracting the mean of each variable, multiplying the deviations, and then dividing by the product of the standard deviations.
• 😀 If data values are predominantly in positive or negative quadrants, the correlation coefficient will reflect a positive or negative relationship, respectively.
• 😀 Hypothesis testing for Pearson correlation assesses whether the correlation in a sample differs significantly from zero to infer the population relationship.
• 😀 For hypothesis testing of Pearson correlation, the variables must be normally distributed to ensure the reliability of the test results.

Q & A

What is Pearson correlation?

Pearson correlation is a statistical measure used to assess the strength and direction of the linear relationship between two variables.

What does a Pearson correlation coefficient of 1 signify?

A Pearson correlation coefficient of 1 indicates a perfect positive correlation, meaning both variables increase together in exact proportion.

How is the direction of the correlation determined?

The direction of the correlation is determined by the sign of the Pearson correlation coefficient. A positive value indicates a positive correlation, while a negative value indicates a negative correlation.

Can Pearson correlation indicate causation between two variables?

No, Pearson correlation only measures the linear relationship between two variables, but it does not imply causation. A correlation does not mean one variable causes the other.

What does it mean if the Pearson correlation coefficient is close to 0?

A Pearson correlation coefficient close to 0 indicates a very weak or no linear relationship between the two variables.

What is the formula for calculating the Pearson correlation coefficient?

The formula is: R = Σ((X_i - X̄)(Y_i - Ŷ)) / √(Σ(X_i - X̄)² Σ(Y_i - Ŷ)²), where X_i and Y_i are the individual data points, and X̄ and Ŷ are the mean values of X and Y, respectively.

What are the assumptions for using Pearson correlation?

Pearson correlation assumes that both variables are normally distributed and that there is a linear relationship between them. If these conditions are not met, the correlation may not be valid.

How is the hypothesis tested when using Pearson correlation?

To test the hypothesis, you compare the correlation coefficient to zero using a t-test. If the p-value is less than the chosen significance level (usually 0.05), you reject the null hypothesis and conclude that a significant correlation exists.

What does a negative Pearson correlation coefficient indicate?

A negative Pearson correlation coefficient indicates an inverse relationship, meaning that as one variable increases, the other decreases.

How does the sample size (N) affect the reliability of Pearson correlation?

The sample size (N) influences the power of the test. A larger sample size provides more reliable estimates of the correlation and increases the likelihood of detecting a significant relationship if one exists.