[Tagalog] Graphing Tangent Functions

Summary

In this video, the presenter dives into the intricate concepts of attention functions and mathematical graphing, with a focus on asymptotes and their role in graphing equations. Throughout, the video explores various techniques for plotting graphs, including understanding the behavior of functions with respect to the origin, positive and negative values, and key terms like reciprocal and amplitude. The presenter emphasizes practical methods for graphing, detailing processes to determine intercepts and handle equations with specific characteristics. The video concludes with an invitation to subscribe for more engaging content and discussions on mathematical principles.

Takeaways

• 😀 The video introduces attention functions and asymptotes, providing a mathematical focus.
• 😀 The script includes a discussion on graphical representations of various functions and their behaviors.
• 😀 Asymptotes are highlighted as an important concept in understanding continuous graphs.
• 😀 The script mentions the use of a formula to divide values by their absolute value to analyze graph characteristics.
• 😀 The explanation includes the concept of the origin and its role in graphing, including intercepts and asymptotes.
• 😀 There is a reference to using coordinate systems and analyzing them through visual representations.
• 😀 The importance of understanding negative and positive behavior in functions is addressed, including how they affect graphs.
• 😀 The video touches upon techniques like the 'easy method' to solve graph-related problems efficiently.
• 😀 The significance of periodicity in functions is emphasized with specific attention to the period and amplitude.
• 😀 The transcript concludes with a thank you message, urging viewers to subscribe and continue engaging with the content.

Q & A

What are asymptotes in mathematics?

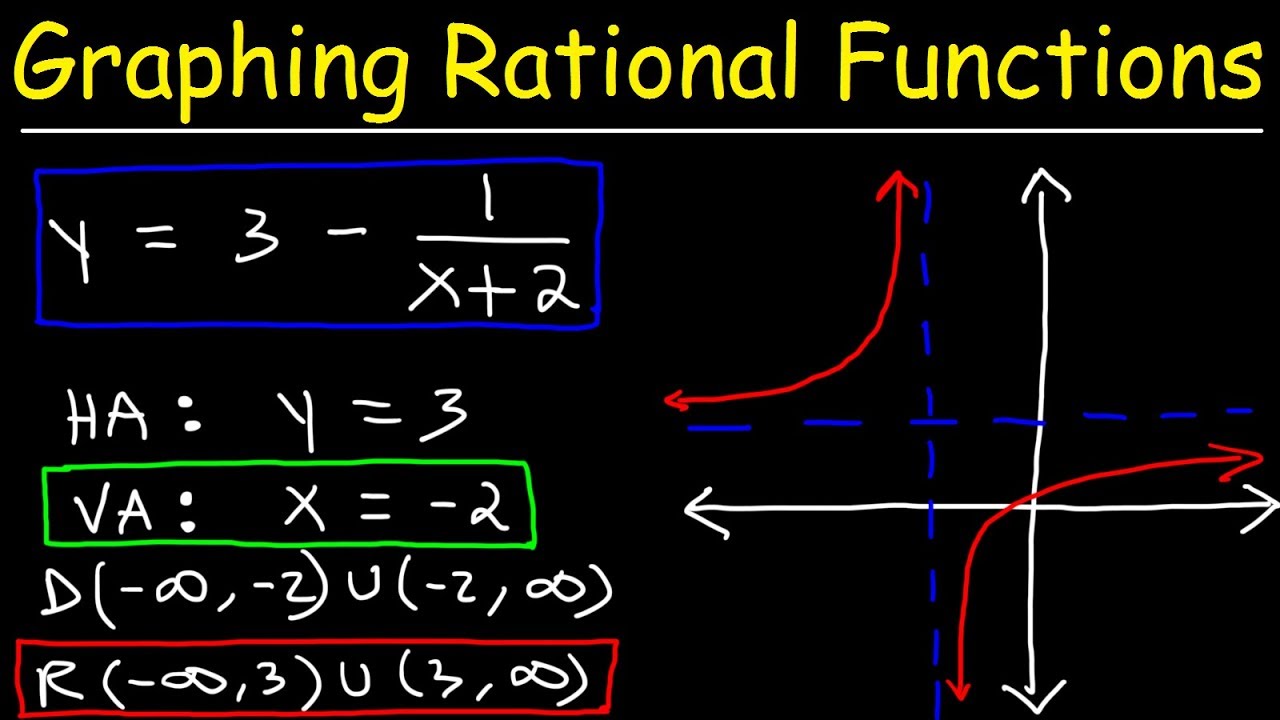
Asymptotes are lines that a graph of a function approaches but never actually touches. They can be vertical, horizontal, or slant, and they describe the behavior of a function as the input (x-value) becomes very large or very small.

What is a vertical asymptote?

A vertical asymptote occurs when the denominator of a rational function equals zero, causing the function to approach infinity or negative infinity as the x-value gets closer to the value where the denominator equals zero.

How do you identify a horizontal asymptote?

A horizontal asymptote is identified by comparing the degrees of the numerator and denominator. If the degree of the numerator is less than that of the denominator, the horizontal asymptote is at y = 0.

What happens if the degree of the numerator is greater than the degree of the denominator?

If the degree of the numerator is greater than the degree of the denominator, the function does not have a horizontal asymptote. Instead, the graph may approach a slant asymptote.

What is a slant asymptote, and when does it occur?

A slant (or oblique) asymptote occurs when the degree of the numerator is one more than the degree of the denominator. To find the equation of the slant asymptote, perform polynomial division.

How do you determine the vertical asymptotes of a rational function?

To determine the vertical asymptotes of a rational function, set the denominator equal to zero and solve for x. The values of x where the denominator is zero are the locations of the vertical asymptotes.

Can a rational function have multiple vertical asymptotes?

Yes, a rational function can have multiple vertical asymptotes if the denominator factors into multiple terms that each equate to zero at different values of x.

What is the horizontal asymptote of the function f(x) = 1/(x^2 - 1)?

The horizontal asymptote of f(x) = 1/(x^2 - 1) is at y = 0, since the degree of the numerator (1) is less than the degree of the denominator (2).

How do you graph a rational function with asymptotes?

To graph a rational function with asymptotes, first identify the vertical asymptotes by setting the denominator equal to zero. Then, determine the horizontal or slant asymptote based on the degrees of the numerator and denominator. Finally, plot a few points and sketch the curve, ensuring it approaches the asymptotes.

Why is it important to understand asymptotes in graphing rational functions?

Understanding asymptotes is crucial for predicting the long-term behavior of rational functions. Asymptotes help determine how the function behaves as the input becomes very large or small, providing a clearer picture of the graph's shape and direction.