REGLA DEL COCIENTE / DERIVADA DE FUNCIONES

Takeaways

• 😀 The script explains the quotient rule for derivatives, which is used when differentiating a division of two functions.
• 😀 The first example demonstrates how to apply the quotient rule to differentiate the function (2x^6) / (3x^2).
• 😀 To use the quotient rule, copy the numerator and denominator, then apply the rule to each part by differentiating the numerator and denominator separately.
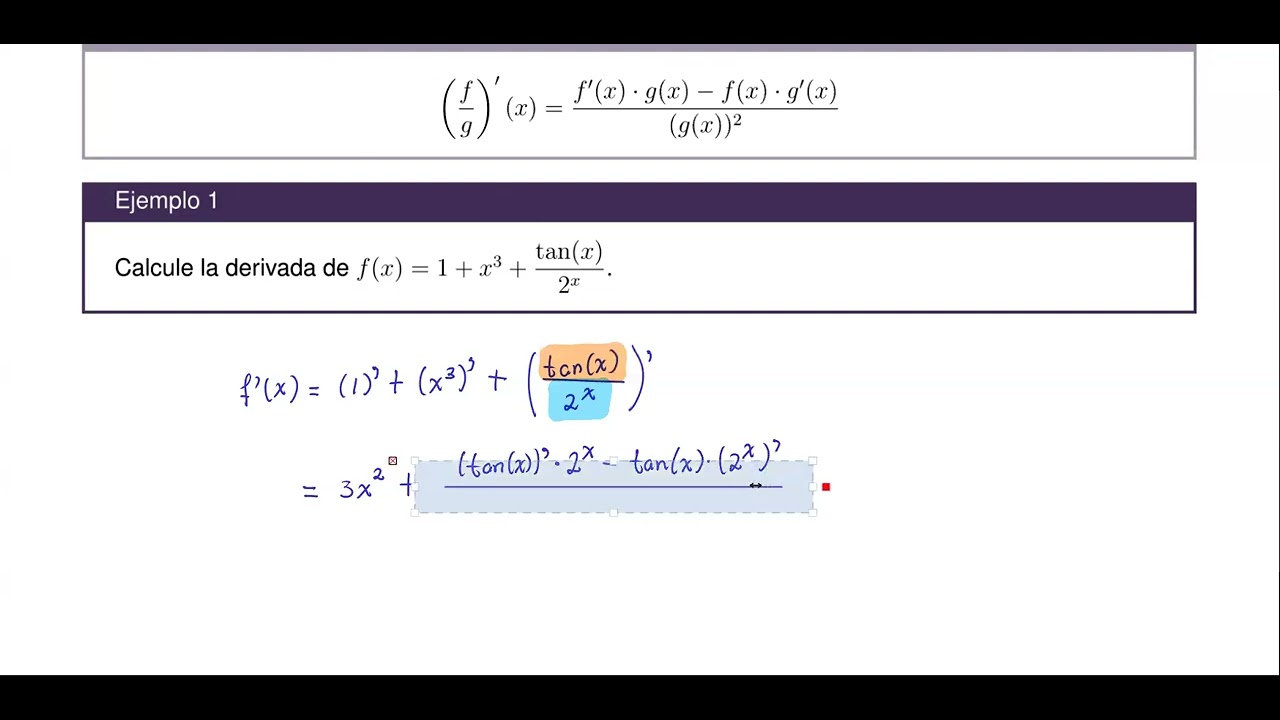
• 😀 The quotient rule formula is: (f'(x)g(x) - f(x)g'(x)) / (g(x))^2.
• 😀 In the first example, the numerator and denominator are differentiated, and simplification is done after the derivatives are calculated.
• 😀 After differentiation, the expression is simplified to obtain the final result for the derivative, which in this case is 8/3 * x^3.
• 😀 The script emphasizes the importance of applying the quotient rule when dealing with functions that can't be simplified directly.
• 😀 A faster alternative to using the quotient rule is simplifying the expression first, but the script focuses on showing the full process for clarity.
• 😀 The second exercise highlights the importance of following the quotient rule when simplification isn’t possible in the expression.
• 😀 The script provides further examples of derivative calculations using the quotient rule and invites viewers to practice additional exercises for better understanding.

Q & A

What is the quotient rule for derivatives?

The quotient rule for derivatives is used to differentiate a function that is the ratio of two other functions. The formula is: (f(x) / g(x))' = (f'(x) * g(x) - f(x) * g'(x)) / (g(x))^2, where f'(x) and g'(x) are the derivatives of the numerator and denominator, respectively.

In the first example, how do we apply the quotient rule to differentiate 2x^6 / 3x^2?

We apply the quotient rule: copy the numerator (2x^6), and the denominator (3x^2), and differentiate both. After simplifying, the derivative of the function is 8x^3/3.

What is the role of exponent rules in simplifying the expression during differentiation?

Exponent rules help when dealing with terms like x raised to powers. For example, when differentiating x^6, the exponent (6) comes down to multiply by the coefficient, and the exponent is reduced by one.

Why does the derivative of a constant like -3 become 0 in the differentiation process?

The derivative of any constant is always 0 because constants do not change with respect to the variable, so their rate of change is zero.

In the second example, what happens when the numerator and denominator cannot be simplified?

When the numerator and denominator cannot be simplified, the quotient rule must be applied directly to differentiate the function, as shown in the second example (2x^4 - 3) / (4x).

How does the derivative of a constant term affect the overall result in the quotient rule?

The derivative of a constant term contributes 0 to the overall derivative, simplifying the expression by removing that term from the derivative.

What is the result after applying the quotient rule to the second exercise (2x^4 - 3) / (4x)?

After applying the quotient rule, the derivative of the second exercise is simplified to (6x^3 + 3) / (4x^2).

In the third example, why does the derivative of -2 become zero?

The derivative of -2 becomes zero because -2 is a constant and, as mentioned earlier, the derivative of any constant is 0.

What is the final result of the third exercise, where the function is -2 / (x + 3)?

The final derivative of the third exercise is 2 / (x + 3)^2, derived using the quotient rule.

What are some potential advantages of using the quotient rule compared to simplifying a function before differentiating?

While simplifying a function before differentiating can sometimes make the process quicker, using the quotient rule directly avoids the need for simplification, especially when dealing with more complex expressions that cannot be simplified easily.