Fluid Mechanics Lesson 15D: Normal Shocks
Summary
TLDRIn this lesson on normal shocks, the behavior of supersonic and subsonic flows across a shock is explored. Using a converging-diverging nozzle as an example, the flow dynamics, pressure, Mach number, and temperature changes across the shock are discussed. The lesson includes analogies such as traffic and coin shocks to simplify the concept. Key equations are presented for calculating changes in pressure, temperature, Mach number, and other thermodynamic properties before and after the shock. A practical example problem is worked through, demonstrating the application of these concepts in real-world conditions.
Takeaways
- 😀 A normal shock is a sudden transition in flow where supersonic flow becomes subsonic, resulting in a sharp change in pressure, temperature, and other properties.
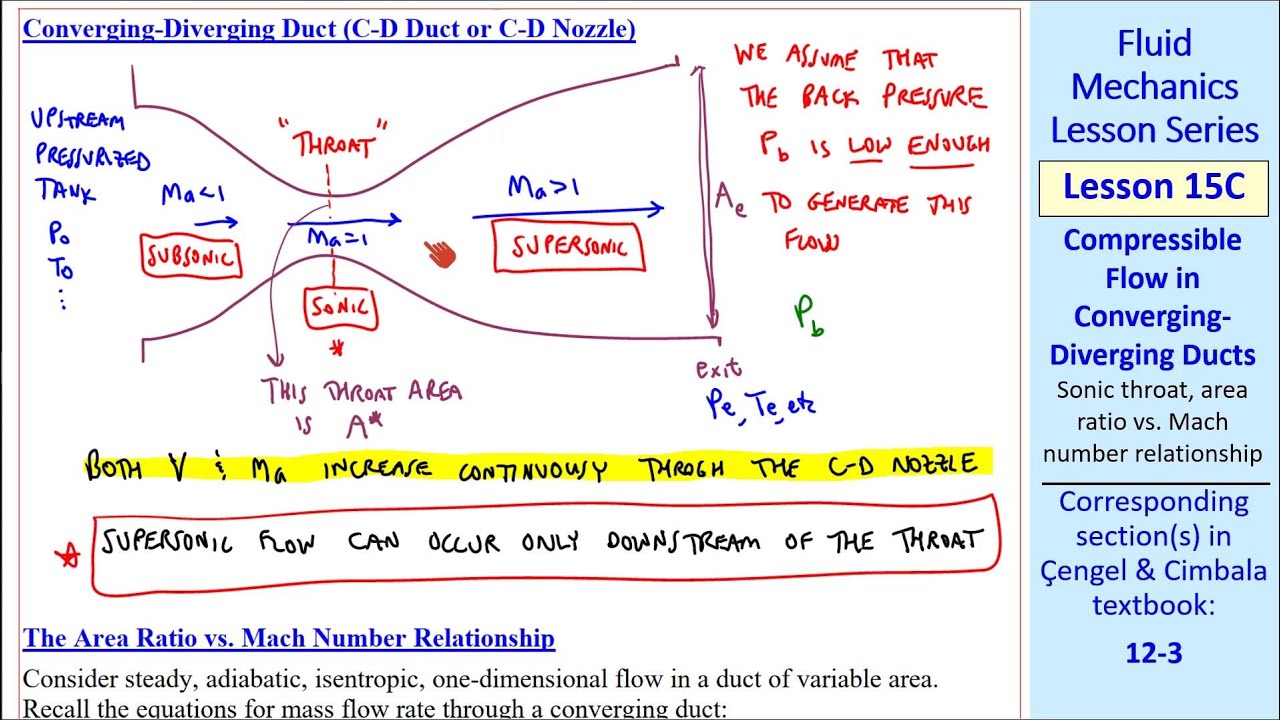
- 😀 In a converging-diverging nozzle, the flow is subsonic before the throat, becomes supersonic after the throat, and then transitions to subsonic again after a normal shock.
- 😀 The shock position is influenced by back pressure (PB) and stagnation pressure (P0). As PB decreases, the shock moves downstream.
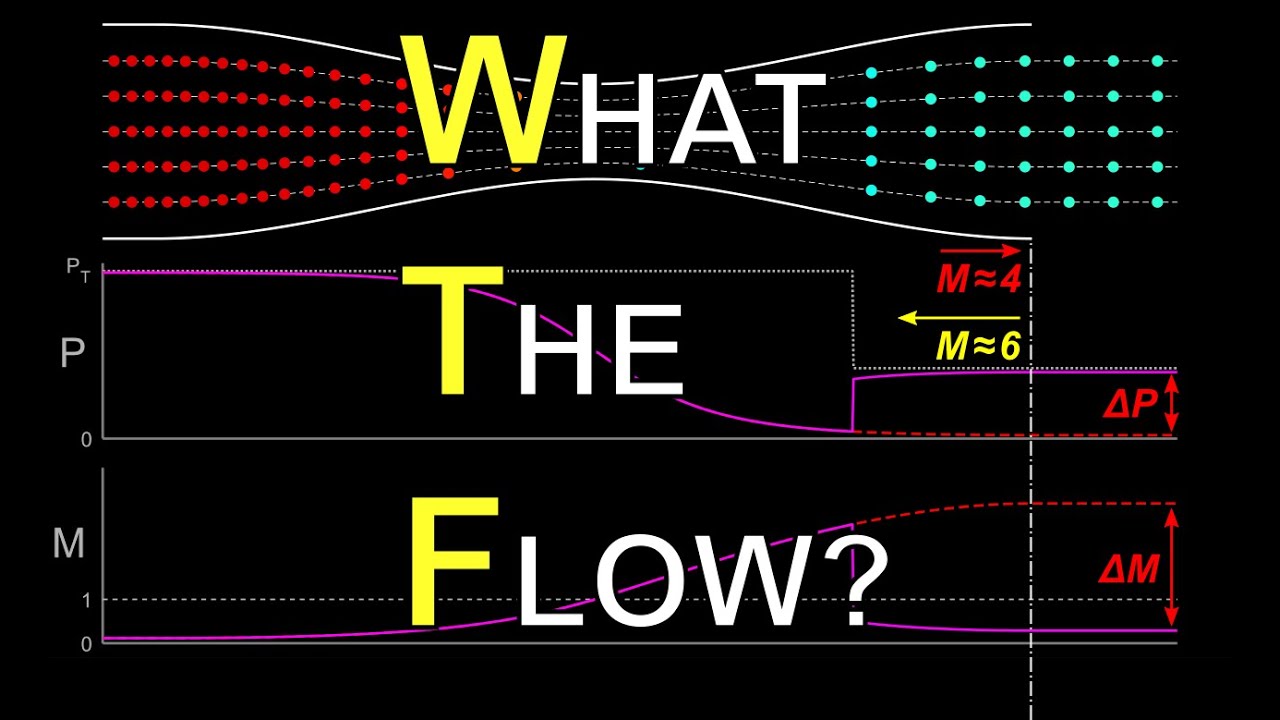
- 😀 A normal shock leads to a sharp increase in pressure, temperature, density, and speed of sound across the shock. The Mach number drops from supersonic to subsonic.
- 😀 Stagnation temperature remains constant across the shock because the flow is considered adiabatic, but stagnation pressure and density decrease.
- 😀 The shock is characterized by an increase in entropy, which makes it irreversible (not isentropic), and this violates the second law of thermodynamics.
- 😀 The strength of the shock increases with Mach number. A higher Mach number upstream results in a greater pressure jump across the shock.
- 😀 Two analogies are used to explain normal shocks: a traffic analogy (cars colliding in a traffic jam) and a coin analogy (coins pushed into a bunch). Both illustrate the sudden compression of the flow across the shock.
- 😀 The Mach number ratio across a normal shock can be calculated using specific equations, with Mach number dropping from supersonic to subsonic after the shock.
- 😀 In practical scenarios, normal shock waves are often seen in devices like converging-diverging nozzles, where the shock helps regulate flow behavior by controlling pressure and velocity.
Q & A
What is a normal shock in fluid dynamics?
-A normal shock is a sudden change in fluid properties where the flow transitions from supersonic (Mach > 1) to subsonic (Mach < 1). It occurs in a converging-diverging nozzle or other fluid flow scenarios and leads to a sharp increase in pressure, temperature, and density, while the Mach number drops across the shock.
How do the properties of a gas change across a normal shock?
-Across a normal shock, the pressure, temperature, density, and speed of sound all increase. The Mach number decreases from supersonic to subsonic values, while stagnation temperature remains constant, and stagnation pressure decreases.
What happens to the Mach number before and after a normal shock?
-Before the shock, the Mach number is supersonic (greater than 1). After the shock, the Mach number drops suddenly to subsonic values (less than 1). This transition is one of the key characteristics of a normal shock.
Why can't a shock exist with a subsonic Mach number upstream of the shock?
-A shock cannot exist with a subsonic Mach number upstream because it would violate the second law of thermodynamics. A shock is an irreversible process that increases entropy, and subsonic flow cannot transition directly into a shock without violating this principle.
What factors determine the location of a normal shock in a nozzle?
-The location of the normal shock is determined by the back pressure (PB) and the stagnation pressure (P₀). As the back pressure decreases, the shock moves downstream, and if the back pressure is low enough, the shock can occur at the nozzle exit.
What is the analogy of a traffic jam used to explain a normal shock?
-The traffic analogy describes a situation where cars are moving at a constant speed, but a stopped truck suddenly causes a traffic jam. As cars hit the truck, they crash and get squeezed together, similar to how the density of air increases sharply across a normal shock. The shock moves like the point of impact in the traffic scenario.
How does the analogy of coins being pushed by a piston relate to a normal shock?
-In the coin analogy, a piston pushes coins, causing them to bunch up as they reach a certain point, analogous to the shock in a gas where the air molecules suddenly compress. The shock moves ahead of the piston, and just like in a shock wave, the coins' density increases abruptly across the shock front.
What properties remain constant across a normal shock?
-The stagnation temperature and stagnation specific enthalpy remain constant across a normal shock, as the shock process is adiabatic. However, other properties such as pressure, temperature, and Mach number change significantly.
How does a normal shock affect the flow in a converging-diverging nozzle?
-In a converging-diverging nozzle, the flow is supersonic before the shock and subsonic after the shock. Before the shock, the nozzle is in a supersonic regime where Mach number increases and pressure decreases. After the shock, the flow becomes subsonic, and the pressure increases, while the Mach number decreases.
What is the formula for Mach number after a normal shock?
-The Mach number after a normal shock (M₂) can be calculated using the equation: M₂ = f(M₁, γ), where M₁ is the Mach number before the shock and γ is the ratio of specific heats. This relationship is derived from conservation laws and shock equations.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
Supersonic Nozzles - What happens next will SHOCK you!
Fluid Mechanics Lesson 15C: Compressible Flow in Converging-Diverging Ducts

Fluid Mechanics Lesson 15B: Compressible Flow and Choking in Converging Ducts

G11S Phy Ch3,4 Emission of sound Vid 1of 3 En 20 21

Materi 6 Topik Aliran Kompresibel

Effects of Fluid Compressibility
5.0 / 5 (0 votes)