Pengolahan Sinyal Digital: 08 Domain Sinyal dan Transformasinya

Summary

This video explores the concept of signal processing, focusing on the transformation of signals from time/space domains to frequency domains and vice versa. It covers key signal transformations, including Fourier, Laplace, and Z-transformations, explaining their relevance for both periodic and non-periodic signals. The video also delves into the differences between analog and digital signals, explaining how they are represented in the frequency domain. Additionally, it demonstrates the practical applications of these transformations for analyzing and reconstructing signals in various systems.

Takeaways

• 😀 Signal representation can be visualized as a function that changes with respect to time or position, like a sinusoidal function.
• 😀 Transforming a signal from the time or space domain to the frequency domain allows analysis of its frequency characteristics.
• 😀 Transformations are used to obtain the frequency domain representation of a signal and vice versa.
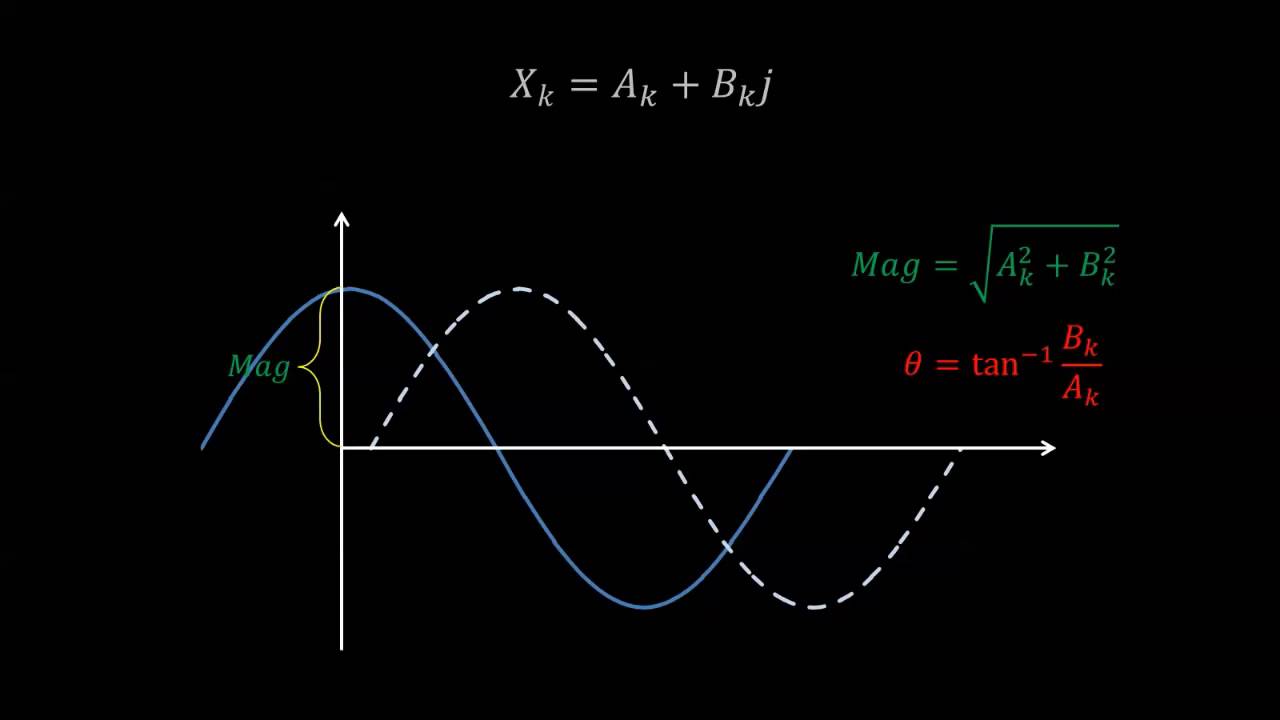
• 😀 The Fourier Transform is used to analyze periodic signals by decomposing them into sums of sine and cosine functions.
• 😀 The Fourier series can be simplified using complex exponentials to represent sinusoidal functions more efficiently.
• 😀 For periodic signals, increasing the number of sinusoidal components improves the approximation of the signal.
• 😀 The Laplace Transform is an extension of the Fourier Transform that includes a complex frequency component to handle signals with exponential growth or decay.
• 😀 The Z-Transform is similar to the Laplace Transform but applies to discrete signals, with a complex frequency domain for analyzing these signals.
• 😀 The inverse transformations (e.g., inverse Fourier or inverse Laplace) are used to revert a signal from the frequency domain back to the time or space domain.
• 😀 The process of matching a signal to a frequency function through transforms helps to identify dominant frequencies in the signal.
• 😀 Different transforms like Fourier, Laplace, and Z-Transforms are selected based on the type of signal being analyzed, whether it's continuous, discrete, periodic, or non-periodic.

Q & A

What is the main topic discussed in this video?

The video focuses on digital signal processing, specifically the concept of signal domains and transformations. It explains how signals can be represented in time or space domains and how they can be transformed into frequency domains for analysis.

What does the term 'signal domain' refer to?

The signal domain refers to the way a signal is represented, either in terms of time or space (e.g., a time-domain signal), or in terms of frequency (e.g., a frequency-domain signal). It is crucial to understand how signals change over time or space and how they can be analyzed in the frequency domain.

What is the process of transforming a signal from time or space domain to frequency domain?

The process of transforming a signal from the time or space domain to the frequency domain is known as signal transformation. This involves converting the signal's function, which depends on time or space, into a function that depends on frequency, providing insight into the signal's frequency components.

What is the inverse transformation in signal processing?

The inverse transformation is the process of converting a signal back from the frequency domain to the time or space domain. This allows us to recover the original signal's time or space representation after it has been transformed into the frequency domain.

What is the significance of using uppercase and lowercase letters in signal representations?

In signal processing, uppercase letters are used to represent signals in the frequency domain, while lowercase letters represent signals in the time or space domain. This distinction helps differentiate between the two domains during analysis and transformation.

What is Fourier series and how is it used in signal processing?

The Fourier series is used to represent periodic signals as a sum of sinusoidal functions (sine and cosine). It allows for the decomposition of complex periodic signals into simpler components, which can be analyzed in terms of their frequency content.

What role does the complex exponential play in Fourier series?

The complex exponential function is used to simplify the representation of periodic signals in Fourier series. By expressing sinusoidal functions as complex exponentials, the analysis becomes more straightforward, as complex exponentials combine sine and cosine functions into a single mathematical expression.

What is the main difference between Fourier Transform and Laplace Transform?

The main difference is that the Fourier Transform analyzes signals in terms of frequency, while the Laplace Transform extends this concept to handle both oscillatory and decaying signals. Laplace Transform uses a complex frequency variable, incorporating both real and imaginary parts (sigma and omega), to capture a wider range of signal behaviors.

What is the Z-transform and how does it differ from the Laplace Transform?

The Z-transform is similar to the Laplace Transform but is specifically used for discrete-time signals. While the Laplace Transform uses a continuous complex frequency variable, the Z-transform uses a discrete complex variable (Z), making it suitable for analyzing discrete signals in the z-domain.

How can the different transformations (Fourier, Laplace, Z) be applied to various signal types?

Each transformation serves different types of signals: the Fourier Transform is used for periodic signals, the Laplace Transform is used for continuous signals, especially those that exhibit exponential decay or growth, and the Z-transform is used for discrete signals, especially in digital signal processing. Each transformation helps analyze the signal's behavior in its respective domain (time or frequency).