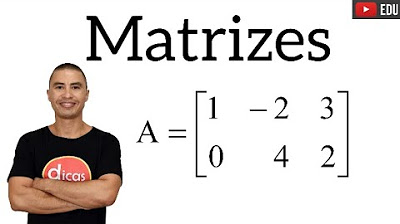Diketahui: (-1 4 -2 3)+(4 -5 -3 2)=(2 -1 -4 3)(2p 1 1 q+1). Nilai p+q= ...
Summary
TLDRThis instructional video delves into the fundamental concepts of matrix addition and multiplication, emphasizing the importance of understanding matrix dimensions. It explains the step-by-step process of adding and multiplying 2x2 matrices, providing clear examples and calculations. The presenter highlights how to derive unknowns from the results, illustrating the application of matrix operations in solving equations. By breaking down complex concepts into manageable parts, the video aims to enhance viewers' grasp of linear algebra, making it accessible and engaging.
Takeaways
- 😀 Understand the basic concepts of matrix addition and multiplication.
- 😀 For matrix addition, combine corresponding elements from two matrices of the same size.
- 😀 The result of adding two 2x2 matrices A and B yields another 2x2 matrix where each element is the sum of the corresponding elements.
- 😀 Matrix multiplication requires that the number of columns in the first matrix equals the number of rows in the second matrix.
- 😀 The resulting matrix from multiplying an m x n matrix with an n x s matrix will have dimensions m x s.
- 😀 When multiplying matrices, multiply rows of the first matrix by columns of the second matrix.
- 😀 The formula for element calculation in matrix multiplication involves summing the products of corresponding elements.
- 😀 Demonstration included calculating the addition of specific matrices, resulting in a new matrix.
- 😀 Explanation of how to set up and calculate matrix multiplication with given matrices.
- 😀 Provided a step-by-step solution to find values of P and Q from the resulting matrix equations.
Q & A
What is the basic concept of matrix addition?
-Matrix addition involves adding corresponding elements from two matrices of the same dimensions. For example, if we have matrices A and B, the element in the first row and first column of the resulting matrix is the sum of the first row and first column elements of A and B.
How do you perform matrix multiplication?
-To multiply two matrices, the number of columns in the first matrix must equal the number of rows in the second matrix. The element in the resulting matrix is calculated by taking the dot product of the corresponding row from the first matrix and the column from the second matrix.
What is the formula for the order of the resulting matrix after multiplication?
-If matrix A has dimensions m x n and matrix B has dimensions n x s, the resulting matrix will have dimensions m x s.
What does the left matrix determine in multiplication?
-The left matrix determines the number of rows in the resulting matrix, while the right matrix determines the number of columns.
How are elements calculated in a matrix multiplication?
-Each element of the resulting matrix is calculated by multiplying the elements of the row from the first matrix by the corresponding elements of the column from the second matrix and summing the results.
What are the steps for adding two matrices given in the script?
-For the example matrices provided, you would add the elements as follows: for the first row and first column, add -1 and 4; for the first row and second column, add 3 and -5; and continue this for all corresponding elements.
What method is used for finding the values of variables P and Q in the script?
-The script suggests equating corresponding elements from the resulting matrix to set up equations that can be solved for P and Q.
What are the final values of P and Q derived from the equations?
-From the equations set up in the script, P is found to be 1 and Q is found to be 2.
What is the significance of the equation P + Q in the context of the problem?
-The equation P + Q, which equals 3, summarizes the combined value of the two variables found from the matrix calculations.
Why is it important to understand the basics of matrix operations?
-Understanding the basics of matrix operations is crucial because these concepts are foundational in linear algebra, which is widely applied in various fields such as computer science, physics, and engineering.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade Now5.0 / 5 (0 votes)