🎡 Velocidad Angular (Movimiento Circular Uniforme) | MCU Video 7
Summary
TLDREn este video se explica cómo calcular el desplazamiento angular de la llanta de un automóvil dado su velocidad angular y el tiempo de rotación. Se presenta que la velocidad angular es de 75 radianes por segundo y que la llanta gira durante 30 segundos. Se utiliza la fórmula del movimiento circular uniforme para determinar que el desplazamiento angular es de 2,250 radianes. Luego, se convierte esta cantidad a vueltas, resultando en aproximadamente 358.5 vueltas. El video concluye invitando a los espectadores a suscribirse y compartir el contenido relacionado.
Takeaways
- 😀 La velocidad angular de la llanta de un automóvil es de 75 radianes por segundo.
- 🕒 El tiempo de rotación de la llanta es de 30 segundos.
- 🔄 Para calcular el desplazamiento angular, se utiliza la relación entre velocidad angular y tiempo.
- 📏 La fórmula para el desplazamiento angular es: desplazamiento angular = velocidad angular × tiempo.
- 🧮 Al sustituir los valores, el desplazamiento angular resulta ser 2,250 radianes.
- 🔄 Una vuelta completa equivale a 2π radianes (aproximadamente 6.2832 radianes).
- 🔄 Para convertir radianes a vueltas, se utiliza un factor de conversión de 2π radianes por vuelta.
- 📊 Al realizar la conversión, 2,250 radianes se convierten en aproximadamente 358.9 vueltas.
- ✅ Se redondea el resultado a un decimal: 358.9 vueltas.
- 👍 Conclusión: La llanta del automóvil dio 358.9 vueltas en 30 segundos.
Q & A
¿Qué información se proporciona al inicio del enunciado?
-Se proporciona la magnitud de la velocidad angular de la llanta, que es de 75 radiales por segundo, y el tiempo de giro, que es de 30 segundos.
¿Qué se necesita calcular a partir de la información dada?
-Se necesita calcular la magnitud del desplazamiento angular de la llanta en el tiempo especificado.
¿Cuál es la fórmula utilizada para calcular el desplazamiento angular?
-La fórmula utilizada es θ = ω × t, donde θ es el desplazamiento angular, ω es la velocidad angular, y t es el tiempo.
¿Qué valores se sustituyen en la fórmula para calcular el desplazamiento angular?
-Se sustituyen ω = 75 rad/s y t = 30 s en la fórmula, lo que resulta en θ = 2250 radianes.
¿Cómo se convierte el desplazamiento angular de radianes a vueltas?
-Se utiliza el factor de conversión de que 2π radianes es igual a 1 vuelta para realizar la conversión.
¿Cuál es el resultado de la conversión de 2250 radianes a vueltas?
-La conversión resulta en aproximadamente 358.5 vueltas.
¿Por qué es importante que las unidades de tiempo en la velocidad angular sean las mismas que las del tiempo?
-Es importante para asegurar la coherencia en las unidades y que los cálculos sean correctos.
¿Qué se concluye al final del cálculo sobre la llanta del automóvil?
-Se concluye que la llanta del automóvil dio 358.5 vueltas en un tiempo de 30 segundos.
¿Qué tipo de movimiento se menciona en la explicación del cálculo?
-Se menciona el movimiento circular uniforme.
¿Cómo se describe la presentación al final del video?
-Se invita a los espectadores a suscribirse y compartir el video, agradeciendo su visita.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

🎡 Velocidad Angular (Movimiento Circular Uniforme) | MCU Video 8

How to calculate angular speed of second, minute and hour hand
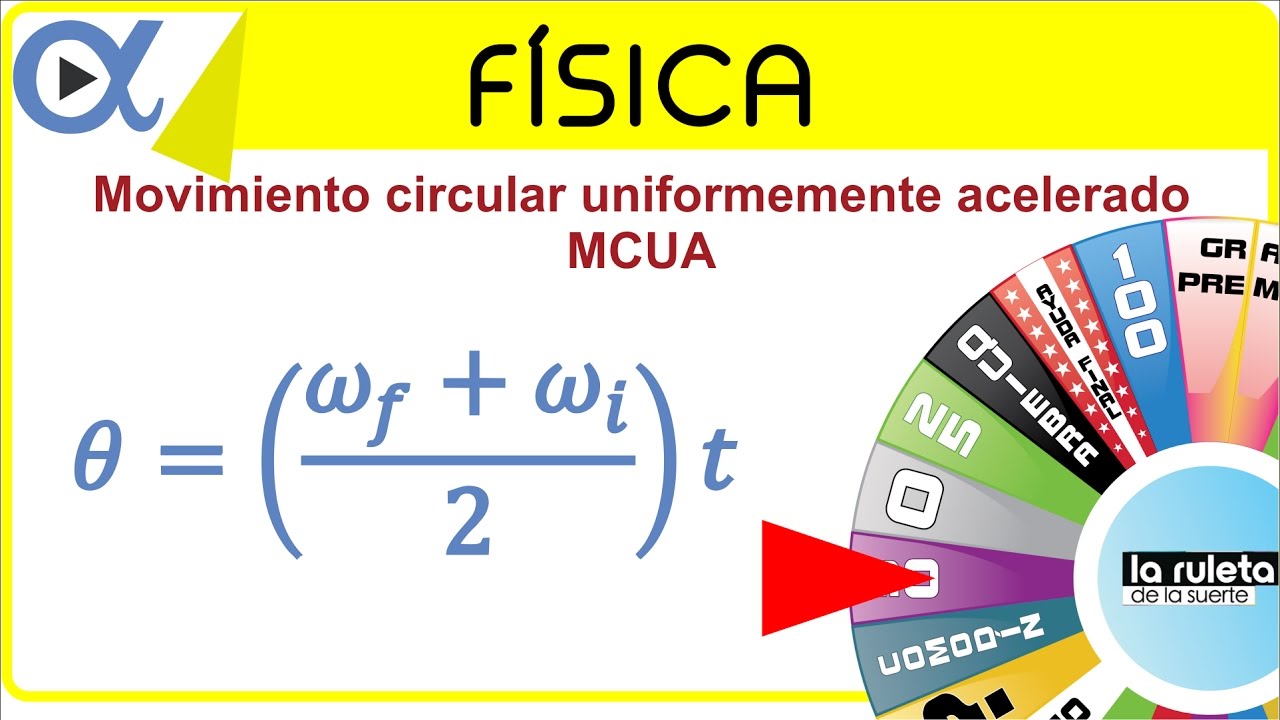
Movimiento circular uniformemente acelerado (MCUA) ejemplo 1 de 5 | Física - Vitual

Período y Frecuencia - MCU - Ejercicios Resueltos

✅MOVIMIENTO CIRCULAR EJERCICIOS | APRÉNDELO AHORA!!💯| FÍSICA PREPARATORIA

Movimiento Circular Uniforme MCU | Calcular rapidez angular y aceleración centrípeta
5.0 / 5 (0 votes)
