Probability - Independent and Dependent Events
Summary
TLDRThis video explores independent and dependent events through a practical probability example involving marbles. It begins by explaining the concepts and demonstrates calculations for selecting marbles of various colors with and without replacement. Key probabilities are derived, showing how event outcomes can change based on whether replacements are made. The video emphasizes the importance of understanding these differences, illustrating how independent events do not affect each other, while dependent events do. This engaging explanation serves as a valuable resource for learners seeking to grasp fundamental probability concepts.
Takeaways
- 😀 Independent events are those that do not influence each other's outcomes.
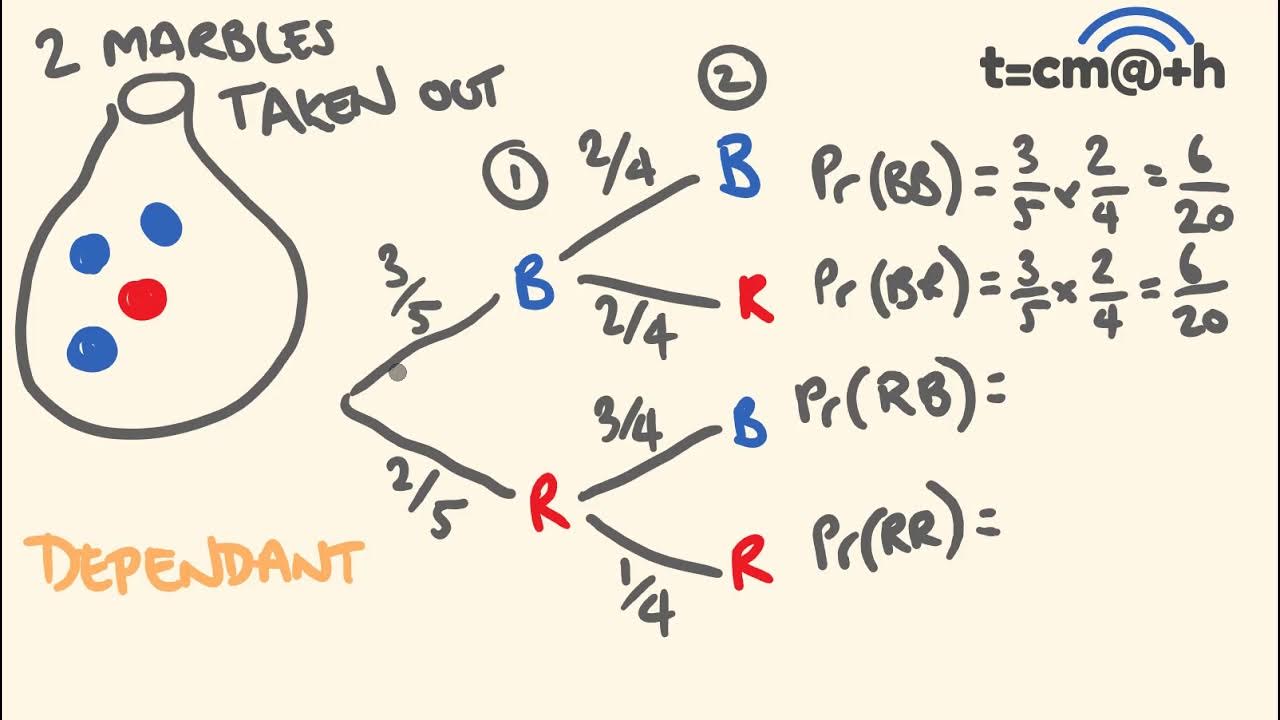
- 😀 Dependent events are those where the outcome of one event affects the probability of another.
- 😀 To calculate the probability of an event, use the formula: favorable outcomes / total outcomes.
- 😀 The total number of marbles in a bag example illustrates how to determine probabilities.
- 😀 When selecting with replacement, the total number of outcomes remains constant.
- 😀 Selecting without replacement reduces the total number of outcomes for subsequent events.
- 😀 The probability of selecting a red marble from a bag with 25 total marbles is 32%.
- 😀 In the blue and green marble example, the events are independent because of replacement.
- 😀 Selecting two blue marbles with replacement results in a 7.84% chance.
- 😀 Selecting two green marbles without replacement demonstrates dependent events with a 5% chance.
Q & A
What are independent events in probability?
-Independent events are events that do not affect each other's probabilities. The occurrence of one event does not influence the outcome of another.
What are dependent events in probability?
-Dependent events are events where the outcome of one event affects the probability of another. The probability of the second event changes based on the outcome of the first.
How do you calculate the probability of selecting a red marble from a bag containing 8 red, 7 blue, 6 green, and 4 yellow marbles?
-The probability of selecting a red marble is calculated by dividing the number of red marbles (8) by the total number of marbles (25), resulting in a probability of 0.32 or 32%.
What is the probability of selecting a blue marble first and then a green marble with replacement?
-The probability of selecting a blue marble is 7/25, and the probability of selecting a green marble remains 6/25 after replacement. Thus, the combined probability is (7/25) * (6/25) = 42/625, or approximately 6.72%.
How does the concept of replacement affect the calculation of probabilities?
-With replacement, the total number of outcomes remains the same for each event, keeping the probabilities constant. Without replacement, the total number of outcomes decreases after each selection, affecting subsequent probabilities.
What is the probability of selecting a yellow marble first and then a red marble without replacement?
-The probability of selecting a yellow marble is 4/25. After removing a yellow marble, the probability of selecting a red marble changes to 8/24. Thus, the combined probability is (4/25) * (8/24) = 4/75, or approximately 5.33%.
In the context of the example, which part represents independent events?
-Part B, which involves selecting a blue marble and then a green marble with replacement, represents independent events because the selection of the blue marble does not change the probability of selecting a green marble.
Which situation in the examples involves dependent events?
-Part C, which involves selecting a yellow marble first and then a red marble without replacement, involves dependent events because the selection of the first marble affects the probability of selecting the second.
What is the probability of selecting two blue marbles with replacement?
-The probability of selecting two blue marbles with replacement is calculated as (7/25) * (7/25) = 49/625, which is approximately 7.84%.
What is the probability of selecting two green marbles without replacement?
-The probability of selecting two green marbles without replacement is (6/25) * (5/24) = 30/600, or 0.05, which equals 5%.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Probability of Independent and Dependent Events (6.2)

Peluang Kejadian Saling Bebas dan Bersyarat (Tidak Saling Bebas)
Probability - addition and multiplication rules

Regla de la multiplicación Probabilidad | Ejemplo 1

Peluang | Matematika Kelas X SMA/SMK FASE E | Materi dan Latihan Soal

PELUANG - Kejadian saling lepas dan tidak saling lepas
5.0 / 5 (0 votes)