Probability - addition and multiplication rules

Summary

This Tech Math video tutorial delves into calculating probabilities across multiple events, using relatable examples like flipping coins and drawing marbles. It introduces viewers to the product and addition rules in probability, explaining how to handle independent and dependent events. The video employs tree diagrams to visually map out possible outcomes and illustrates how to multiply probabilities for independent events and add them for mutually exclusive ones. It also covers scenarios with and without replacement, highlighting the impact on probability calculations. The host encourages interaction, inviting viewers to try examples and providing a call to action for likes and subscriptions.

Takeaways

• 🎓 The video discusses calculating probabilities over multiple events, such as flipping a coin multiple times or drawing marbles from a bag.
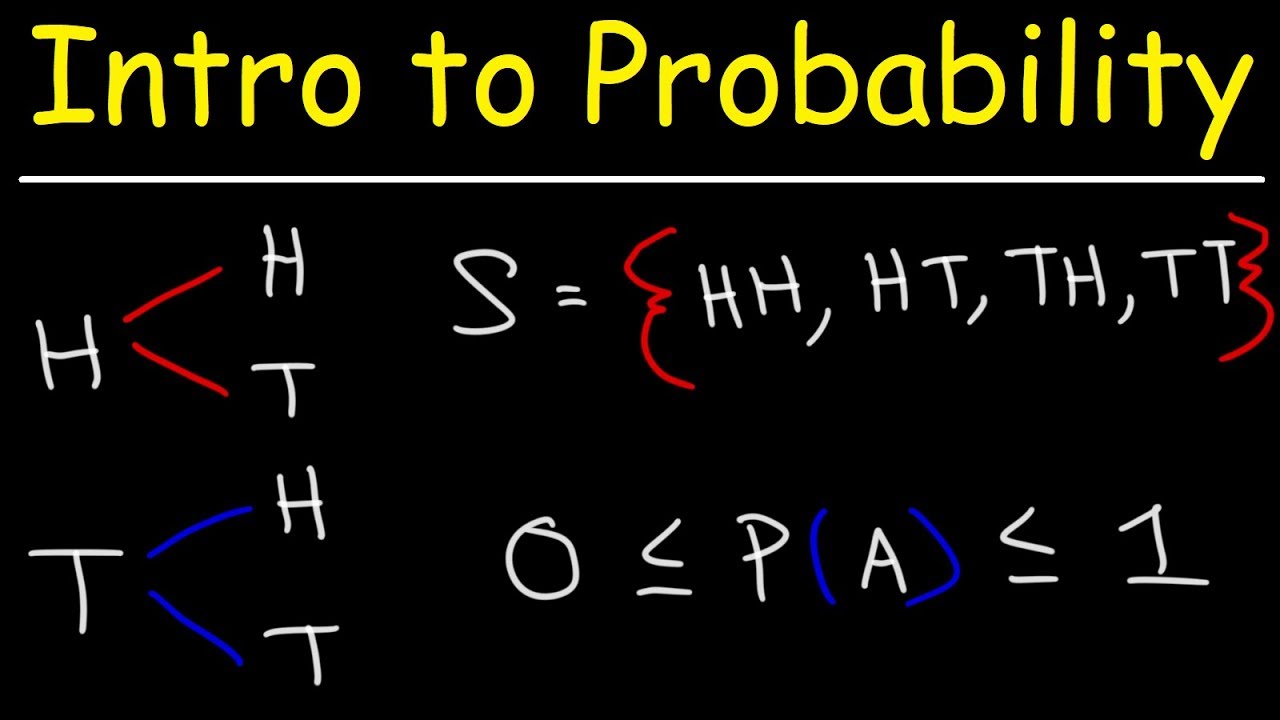
• 📊 A tree diagram is introduced as a method to visualize the different outcomes of multiple events.
• 🔄 The concept of independent events is explained, where the outcome of one event does not affect the probability of another.
• 🔗 The product rule in probability is introduced, which states that the probability of multiple independent events occurring together is found by multiplying their individual probabilities.
• 🔄 The video also covers dependent events, where the outcome of one event affects the probability of subsequent events.
• ➕ The addition rule in probability is explained, which is used to calculate the total probability of multiple mutually exclusive events occurring.
• 🎯 Examples are given to illustrate how to apply the product and addition rules in different scenarios, such as drawing marbles with and without replacement.
• 🍎 A practical example involving selecting apples from a batch with both good and bad ones is used to demonstrate the application of probability rules.
• 🧮 The importance of understanding whether events are independent or dependent is emphasized, as it affects how probabilities are calculated.
• 📈 The video encourages viewers to practice calculating probabilities by working through the examples provided.
• 👍 The presenter prompts viewers to like and subscribe for more content, and mentions the availability of merchandise and Patreon support for the channel.

Q & A

What is the main topic of the video?

The main topic of the video is understanding how to calculate probability over multiple events, including the use of product and addition rules in probability.

What is an example used in the video to explain probability?

An example used in the video is flipping a coin twice and calculating the probability of getting heads both times.

What is the probability of getting two heads when flipping a fair coin twice?

The probability of getting two heads when flipping a fair coin twice is 1/4, as each flip is an independent event with a 1/2 chance of getting heads.

What is the product rule in probability as explained in the video?

The product rule in probability states that the probability of two or more independent events occurring together is calculated by multiplying the individual probabilities of each event.

How does the video demonstrate the addition rule in probability?

The video demonstrates the addition rule by showing that if you have two mutually exclusive events that can occur in different orders (like getting a head then a tail or a tail then a head), you add the probabilities of each sequence to find the total probability.

What is the difference between independent and dependent events as discussed in the video?

Independent events are those where the outcome of one event does not affect the probability of the other event. Dependent events are those where the outcome of one event changes the probability of the other event.

Can you explain the marble drawing example used in the video?

The marble drawing example involves a bag containing three blue and two red marbles. The video explains how to calculate the probability of drawing two marbles of the same color, considering both dependent (without replacement) and independent (with replacement) scenarios.

What is the significance of replacement in the context of the marble drawing example?

Replacement signifies that after drawing a marble, it is put back into the bag, thus keeping the total number of marbles constant and making each draw independent of the others. Without replacement, the probabilities change after each draw because the total number of marbles decreases.

How does the video handle the scenario of drawing two marbles with replacement?

In the scenario with replacement, the video shows that the probabilities remain the same for each draw because the marble is put back, making each event independent and not affected by previous draws.

What is the final example given in the video, and how does it relate to probability?

The final example is about drawing two apples from a group of six, where three are good and three are bad. The video uses this to illustrate calculating the probabilities of drawing different combinations of good and bad apples, emphasizing the concept of dependent events.

Outlines

00:00

🎓 Introduction to Probability in Multiple Events

The video begins with an introduction to the concept of probability over multiple events, using examples like flipping a coin twice and drawing marbles from a bag. The host explains that probabilities can be calculated for multiple events using product and addition rules, and discusses the difference between independent and dependent events. A tree diagram is introduced as a tool to visualize the outcomes of flipping a coin twice, emphasizing the independence of each flip with a probability of 1/2 for heads or tails. The product rule for probability is introduced, which states that the probability of multiple independent events occurring together is found by multiplying their individual probabilities.

05:01

📊 Probability Calculations with Tree Diagrams

This section delves deeper into using tree diagrams to calculate probabilities for different sequences of events, such as getting heads or tails in a coin flip. The video explains the product rule for multiple events, where the probability of a sequence of events is found by multiplying the probabilities of each event. It also introduces the addition rule for mutually exclusive events, where the total probability is found by adding the probabilities of each possible sequence. The host uses the example of drawing marbles from a bag to illustrate these concepts, showing how to calculate the probabilities of drawing two blue marbles, two red marbles, or one of each, considering both dependent and independent events.

10:01

🔄 Impact of Replacement on Probability

The video explores how the concept of replacement affects probability calculations. It contrasts two scenarios: drawing marbles with and without replacement from a bag. The host explains that without replacement, the probabilities of drawing certain colors change after each draw because the total number of marbles and their proportions have changed. This leads to dependent events where the outcome of one draw affects the next. In contrast, with replacement, the probabilities remain the same for each draw, treating the events as independent. The video uses examples to demonstrate how to calculate probabilities in both scenarios, emphasizing the importance of understanding whether replacement occurs.

15:04

🍎 Applying Probability Rules to Real-World Scenarios

In the final part of the video, the host applies the discussed probability rules to a real-world scenario of drawing apples, some good and some bad, from a collection without replacement. The video demonstrates how to calculate the probability of drawing different combinations of good and bad apples using the product rule for dependent events. It also shows how to find the probability of drawing at least one good or one bad apple using the addition rule for mutually exclusive events. The host encourages viewers to practice these calculations on their own before revealing the solutions, reinforcing the learning with practical examples.

Keywords

💡Probability

Probability refers to the measure of how likely an event is to occur. In the video, probability is calculated over multiple events, such as flipping a coin or drawing marbles from a bag. For instance, the probability of flipping heads twice in a row is explained through the use of the product rule.

💡Independent Events

Independent events are events where the outcome of one event does not affect the outcome of another. In the video, the presenter explains that flipping a coin is an independent event because the result of the first flip doesn't influence the result of the second flip. For example, the probability of flipping heads on the first flip remains the same as on the second flip.

💡Dependent Events

Dependent events are events where the outcome of one event affects the probability of subsequent events. The video discusses drawing marbles from a bag without replacement as an example of dependent events, since removing one marble changes the total number of marbles left, altering the probabilities for the next draw.

💡Product Rule

The product rule is used to calculate the probability of two or more independent events happening together by multiplying their individual probabilities. For instance, the probability of getting heads twice in a row when flipping a coin is calculated by multiplying 1/2 by 1/2, resulting in a 1/4 probability.

💡Addition Rule

The addition rule is used when calculating the probability of mutually exclusive events happening. In the video, it is explained that if you want to calculate the probability of getting either a head then a tail or a tail then a head when flipping a coin, you add the probabilities of these two events together.

💡Tree Diagram

A tree diagram is a visual tool used to represent all possible outcomes of a sequence of events. The video uses tree diagrams to illustrate different probabilities when flipping a coin or drawing marbles, showing how each branch represents a potential outcome and its associated probability.

💡Mutually Exclusive Events

Mutually exclusive events are events that cannot happen at the same time. In the video, the presenter mentions that getting heads and tails on the same flip are mutually exclusive events because only one can occur at a time, leading to the use of the addition rule to calculate the overall probability.

💡Without Replacement

Without replacement refers to situations where once an item (such as a marble) is taken, it is not returned to the pool for subsequent events. This is an example of dependent events, as removing a marble changes the probabilities of future draws. The video contrasts this with scenarios where the item is replaced, keeping the probabilities independent.

💡With Replacement

With replacement refers to a situation where, after drawing an item (like a marble), it is returned to the original pool before the next draw. This ensures the events remain independent. In the video, this concept is used to contrast with scenarios where items are not replaced, altering the probabilities for future draws.

💡Multiple Events

Multiple events refer to a sequence of events whose probabilities are considered together. The video explores the probability of various outcomes over multiple events, such as flipping a coin twice or drawing marbles twice, demonstrating how independent and dependent events are handled in probability calculations.

Highlights

Introduction to calculating probability over multiple events.

Example of flipping a coin twice and calculating the probability of getting heads.

Explanation of using a tree diagram to visualize probability outcomes.

Understanding independent events in probability with coin flips.

Product rule in probability: Multiplying probabilities of independent events.

Calculating the probability of getting two heads in a coin flip.

Addition rule in probability: Adding probabilities of mutually exclusive events.

Example of drawing marbles from a bag and calculating probabilities.

Dependent events in probability: Events where outcomes affect each other.

Calculating probabilities with replacement versus without replacement.

Tree diagram for calculating probabilities of drawing marbles with replacement.

Calculating the probability of getting two blues or two reds with replacement.

Tree diagram for calculating probabilities of drawing apples with and without replacement.

Calculating the probability of getting a good and a bad apple without replacement.

Using the product rule to calculate the probability of getting a specific sequence of events.

Using the addition rule to calculate the probability of getting at least one of two events.

Encouragement for viewers to practice calculating probabilities with the provided examples.

Transcripts

good day welcome to the tech math

Channel what we're going to be having a

look at in this video is how to work out

probability over multiple events an

example of this so say you maybe had a

coin and you flipped it and you wanted

to know how many different times you

would get head so you're going to flip

it twice uh did you could you get heads

twice okay so heads and then heads again

and what would be the probability of

that or for maybe for example what we'

be having a look at is we had a bag of

marbles like we have here uh had you

know three blue marbles and three red

marbles and what would be the

probability if we would to draw out two

Marbles and may be getting both of them

being read and so we're going to be

looking at these types of questions okay

what you're going to notice with these

is these probabilities occur over

multiple events and they're easy to work

out um we just got to keep in mind a few

things in this video we're going to be

have a looking at at some of these sort

of things so we're going to be looking

at product and addition rules in

probability as well as events how they

can be independent or dependent on each

other and how these affect uh our

calculations so let's just get on and

have a look at these with a few examples

and don't forget if you like this video

don't just sit there and lightly caress

the like button actually smash that like

button Smash It hey and if you haven't

subscribed already please subscribe

anyway I'm just going to look at a few

examples okay for the first example

we're going to have a look at this we're

going to be considering flipping a coin

twice and just having a bit of a look

about how we might work out various

probabilities of outc that might occur

so to illustrate this a really good way

would be a tree diagram so we have our

first

flip and we could get two possible

outcomes we get a head or a tail so we

get a head or a tail this would be our

first flip we have a second flip where

we have also two possible outcomes we

get once again a head or a tail or we

could have got a tailes first and we

could get a head or a tail now just a

couple of things which is really

important to probably get at this stage

um which is this what you're going to

notice the probability of each event

occurring a probability of getting a

head is one and two the probability of

getting a tail is one and two and so our

first flip here the probability of

getting your head is one and two the

probability getting a tail is one and

two we would consider our second flip

you probably notice really quickly that

it's also the probability of getting

aead here is a one and and the

probability of getting a tail here is

one and two that is to say that these

particular events in the second flip are

independent of the first I actually

going to write that down that's a really

important thing to get this word here

that this is

independent okay uh that each

particular uh outcome or each

probability is independent or each event

is independent of the other event okay

it's not affected by it so we have a

half chance of this occurring and a half

chance of this occurring okay so you can

see this so far we've set this up and

it's all pretty nice so what is the

probability of this happening what is

the probability of getting ahead then

ahead we can use our probabilities here

to work this out okay because the

probability getting ahead at the start

is equal to a half and the probability

of getting so this particular thing here

we could get a head here and we can get

a head here and the probability getting

the second one is also

half now this gets to a first rule of

probability with multiple events and

that's the product rule pretty much the

probability of two or more events

occurring together can be calculated so

two or more events getting ahead and

getting ahead can be calculated simply

by multiplying these individual

probabilities okay so the probability 1

* 1 is 1 2 * 2 is 4 the probability of

getting two heads is one and

four okay what about the probability of

getting uh Tails tails and Tails you'll

probably look at this and go okay it's

the same sort of thing the probability

of getting a tails is a half the

probability of getting a tails is also a

half and so we're talking about this

event followed by this event we're going

to multiply these this is a one in four

chance okay I'm just going to take this

one step further and show you a

different rule in this just give myself

a bit of space here so I'm going to get

rid of these two probabilities here and

we're going to talk about a different

thing that might occur what about the

probability of getting one head and one

tail but not necessarily in that order

it might be uh tail and a head or head

and a tail and you're going to see to do

that we actually have two different ways

that can occur we could first off get a

head and then a tail or we could get a

tail and then a head so I'm going to

write both of these ones down so first

off if we go head tail the probability

of getting that is a half of getting

that first head and then a half you

might say okay we're going to multiply

those because they're in a you know that

particular this event followed by this

event we're going to multiply this this

is a one in4 chance of getting a head

then a tail the chance of getting a tail

than a head is also a halftimes a half

okay a half time a half which is equal

to a quarter so this gets to our second

rule when we're looking at multiple

events probability is this if we're

talking about um two events that are

mutually exclusive that are not

affecting one another we're trying to

find out the total probability say of

something like uh with a tail on a head

here and there's a couple of different

ways this can occur for our outcomes

what we do is we're going to add these

we're going to add our quarter and our

quarter to get the total probability

because the head and the tail is the

same as a tail and a head so what's a

quarter plus a quarter you'd probably

look at it and say okay that's 24

okay so the probability of that

occurring is 2 qu okay or a half so

something to be aware of okay so that's

the product rule where we multiply these

if we're looking at something occurring

in a line like that and if we've got

something which is occurring you know

and we're saying it's uh we want this

and this occurring we're going to add

them together okay that's the addition

rule so I'm going to go through another

example and show you just a variation of

this all right in this example what

we're going to have a look at is we have

a bag and it has three blue marbles and

two red marbles and we're going to take

two marbles out now we're going to work

out also now what our different

probabilities or different outcomes

could be and the probabilities of those

outcomes occurring so once again let's

draw up a tree diagram so we have that

first event where we're taking out the

first marble okay so the first marble

you'll probably look at and say okay we

could either end up with a blue marble

or we could end up with a red marble so

we do that then we're going to pull out

the Blue Marble we get rid of that for

instance and then the next event what we

could do is we might end up with a blue

marble or a red marble or for the when

get a red one first we could end up with

a blue marble or a red marble okay so

let's have a bit of a look here about

the various probabilities of each

individual part here now this is

something to be very very aware of

because the probability of each event is

not independent okay each probability is

each particular event is not independent

of the other I'll show you what I mean

by that so say for instance I pull this

first Blue Marble out you can probably

guess okay there's three blue marbles

out of a total of five marbles for the

Reds there is two out of five over two

five chance of getting a red marble

first that's for our first removal for

the second one what you might notice is

this if I was to remove okay we pick a

blue marble and we get rid of it now

what's the actual probability getting a

Blue Marble now because these are not

independent they are dependent on one

another this actually now depends the

probability of this depends on what

happened here we have two blue marbles

now out of a possible four and to get a

red we have two out of

four okay maybe that didn't happen and

maybe what happened instead is we went

down here and we picked a red out first

so we got rid of a red what's the

probability of getting a Blue Marble

there's three out of four the

probability getting a red is 1 out of

four and this is an example of a

dependent I'll write that down these are

where we

have uh different events that are

dependent on each other dependent okay

and it's something to be really really

aware of because it changes these

probabilities as we go bit of a hint

here what you might see is occasionally

you'll see this described as two t

marbles are taken out without

replacement if they say they are

replaced what we're talking about is the

marbles get put back in and what it

would mean is that we would end up uh

with a independent type scenario okay

where we'd end up with still five

marbles in here so it wouldn't really

affect these later ones and it wouldn't

affect the probabilities here so you'll

probably notice here that we can work

out probabilities here what's the

probability of getting uh two

blues or I'm going to go through each

one of these what's the probability of

getting a blue and a red what's the

probability of getting a red and a

blue red and a blue what's the

probability of getting a red and a

red okay let's have a quick look at

these and these are all going to end up

being product ones we're going to

multiply these we go on the product you

know we got a three and five chance of

getting the first

blue we have a two and four chance of

getting the second

blue multiply these here 2 * 3 is equal

to 6 5 * 4 is equal to 20 now I know we

could simplify this further I'm going to

leave that to you I'm not going to do

that right now because let's face so I'm

going to run out of space if I do that

what about the probability of getting a

blue then a red there's a three and a

five chance of getting the blue and to

get this red here there's a two in four

chance so this also is a 6 and 20

probability this one here we have a two

in five chance of getting a red first

and then a blue we have a three and four

chance going to multiply those we end up

with a once again a 6 out of 20

probability to get two Reds there's a

two in five chance at the start of

actually getting the first red and then

there's a one in four chance of getting

that one a second red so 2 * 1 is 2 over

20 you're going to notice 2 plus 6 plus

6 plus 6 adds up to 20 so all our

probabilities are there and that's a

product uh product rule in action there

now I might also say okay we could

actually do this a little bit

differently and maybe I say okay what

about a blue and a red but not in any

particular order you go okay well we'd

have to add the 6 out of 20 okay I'll

even write this down here I'm going to

be struggling for space anywhere I'm

going to rub this out I reckon I'll put

it

here what's the

probability of the one red and one blue

you can sit there and go okay well we

got two ways this could happen we could

get a blue and a red which is a 6 out of

20 and we've got a red and a blue which

is a 6 out of 20 and we're going to add

these okay this is a 12 out of 20

probability of

occurring okay so this is an example of

a dependent event okay where an event

actually changes the probabilities of

each little part here and something to

be wary of what about one more example

okay I'm going to not vary this one up

too much because I think it maybe it's a

good idea to do this at this stage we're

going to go two marbles taken out same

sort of bag we have two Reds and three

blues but this time with replacement and

let's see what happens okay so if we

take it the Blue Marble first you have a

three and five chance to get a red

marble in the first drawing you have a

two in five chance now imagine we uh

take this Blue Marble out here we go

we're going to take it out but it's

going to get replaced okay so that means

we're putting it back in so I've taken

it out but now I'm putting it straight

back in So what's the chance now of

getting a blue marble and you go okay

well it's still actually three out of

five and to get a red is 2 out of five

okay you're going to notice the actual

probabilities are not changing here and

we almost treat this event well we not

almost we exactly treat this event as

independent because these outcomes here

are not affected these events here are

not affected by this previous event this

would be a 3 out of five and this would

be a 2 out of five and so hence our

overall probabilities would change you

remember this our probability of getting

now say a blue and a

blue is we're going to multiply these

through it's going to be three out of

five * 3 out of 5 which is going to be 3

* 3 is 9 over 25 uh we got a probability

of getting say a blue and a red a blue

and a red is going to be equal to 3 out

of five * 2 out of 5 which is going to

be 6 out of 25 okay notice the

probabilities are all of a sudden

different the probabilities of getting a

red and a blue is equal to 2 out of 5 *

3 out of 5 2 out of 5 * 3 out of 5 which

is going to be equal to 6 out of 25 the

probability of getting a red and a red

is equal to 2 out of

five time 2 out of five which is going

to be 4 out of 25 so be really really

careful of these when you do these that

if it's replacement that you are going

to treat it differently to if it's not

replaced okay uh so you know you can

actually now say okay what's the

probability you can already say what's

the probability of two blues or two Reds

is maybe the probability of um

at

least one

blue what's the probability of this well

this one has at least one blue this one

has at least one blue this one has at

least one one blue uh it's out of 25

because we're going to add all these

together so 25 25 25 the denom staying

the same 9 + 6 + 6 is 12 uh we have 21

it's 21 out of 25 probability

I tell you what we'll do one more okay

in this example what we're going to have

a look at is a scenario we have six

apples where three of them are good and

three of them are bad and we're going to

take two out at random okay so let's

draw up our tree here we have good bad

that's our first one we have good bad

good bad I reckon you should give this a

go without waiting for me by the way

we're going to take these out at random

and remember we're not actually putting

them back there is no replacement so

what I recommend you go through first

can you work out the probability ities

of each of these particular outcomes of

getting a probability of getting a good

good the probability of getting a good

bad the probability of getting a bad

good and the probability of getting a

bad bad and I'll leave that one we we'll

see how we go with those ones uh go for

it so first off go through and work out

your probabilities of each particular

event and then go from there using those

product rules okay so give it a fly

hopefully you did all right okay the

probability of getting a good apple to

start off with is three out of six or a

half it's three out of six here as well

um if you choose a good apple first uh

I'm just going to say we choose one of

these uh we'll get rid of

it so what's our probability now of

getting a good apple you might say okay

it's 2 out of five the probability

getting a bad apple is three out of five

because these are actually uh dependent

particular dependent events here okay

well maybe that didn't happen maybe my

Apple was okay and there it is and

instead what we did is we took a bad

apple out first okay let's have a look

at what happens here you know the

probability of getting a good apple is

now going to be three out of five we

have three Good Apples out of five

apples the probability getting a bad

apple is going to be two out of five

okay what's our different probabilities

here probably getting uh two Good Apples

is 3 out of 6 * 2 out of 5 we just

following up that pathway there 3 2 are

6 uh 65 to 30 what's the probably

getting a good in a badge you might go

okay that's a 3 out of 6 * 3 out of 5

which is going to be 33's and 9 out of

30 the probability getting a bad than a

good we

have uh 3 out of 6 * 3 out of 5 3 out of

6 * 3 out of 5 which is going to be 9

out of 30 also and the prob getting two

bads is 3 out of 6 * 2 out of 5 3 out of

6 * 2 out of 5 which is going to be 6

out of

30 there you go how'd you go with that

now if I was to say once again what's

the probability getting a good apple and

a bad apple you probably go okay and I

might say now what's the probability of

getting a good apple and a bad apple and

you might say okay in any order we could

add these two together 9 out of 30 + 9

out of 30 would give us at least getting

a good apple and getting a bad apple

would give us an 18 out of 30

probability anyway look hopefully you

found this to some use that's uh the

product Edition rules multiple uh

probability uh events there hopefully

this video was some help to you if it

was please like it please subscribe hey

look I'm going to put a dodgy dodgy call

out there there is merch there is

patreon please please support the uh

Tech math Channel all the the more I can

uh get supported there the more free

math I can get out there look I'm going

to keep making it anyway but your

support would be lovely anyway you're

also going to see I'll be putting up

feeds um asking what videos do you guys

want M and you might have a particular

preference and if you do you know put

them up there and I'll look out uh

making them in the future anyway thanks

for watching see you next time bye