Peluang | Matematika Kelas X SMA/SMK FASE E | Materi dan Latihan Soal

Summary

In this educational video, viewers learn about probability concepts such as sample spaces, sample points, mutually exclusive and independent events, and compound events. The lesson explains how to calculate probabilities using real-life examples like coin tosses, dice rolls, and drawing marbles from a bag. The video provides clear explanations of events, along with various practice problems and solutions, including how to compute expected frequencies. With step-by-step guidance, the video helps students grasp foundational probability concepts while reinforcing their learning through practical examples and exercises.

Takeaways

• 😀 Understanding probability involves determining the likelihood of an event occurring based on possible outcomes.
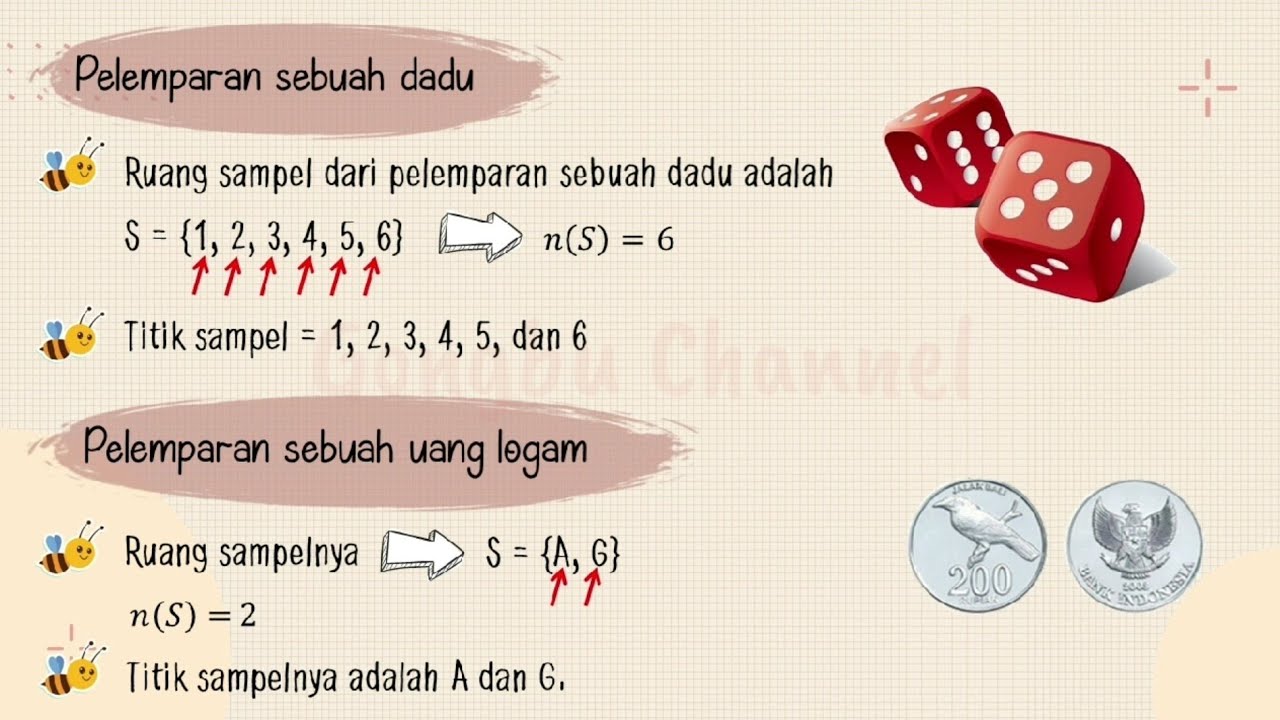
• 😀 The sample space (S) is the set of all possible outcomes in an experiment, e.g., when tossing a coin, S = {H, T}.
• 😀 A sample point is an individual outcome from the sample space, e.g., 'Heads' or 'Tails' for a coin toss.
• 😀 Mutually exclusive events are events that cannot occur at the same time, e.g., tossing 'Heads' and 'Tails' simultaneously is impossible.
• 😀 Independent events are events that do not affect each other's probability, e.g., tossing a coin and rolling a die are independent.
• 😀 When calculating the probability of a compound event, the formula P(A and B) applies to independent events and P(A or B) applies to mutually exclusive events.
• 😀 Venn diagrams are useful tools for visualizing compound events, showing unions (OR) and intersections (AND) between events.
• 😀 The expected frequency of an event can be calculated using the formula: Expected Frequency = Probability × Number of Trials.
• 😀 In the example of drawing marbles from a bag, the sample space depends on the colors of the available marbles.
• 😀 The probability of multiple events occurring together can be calculated by considering all possible combinations of outcomes, e.g., for tossing multiple coins or rolling multiple dice.
• 😀 Compound events can be represented using different combinations of outcomes, such as {2, 3, 4, 5, 6} for 'even' or 'prime' numbers on a die.

Q & A

What is the definition of a sample space in probability?

A sample space is the set of all possible outcomes of an experiment. It is denoted by 'S' and represents the total number of possible results.

What does 'S' represent in the context of a coin flip?

In the context of a coin flip, 'S' represents the sample space, which includes the possible outcomes: heads (G) and tails (A). So, S = {G, A}.

What is the difference between independent and mutually exclusive events?

Independent events are those where the occurrence of one event does not affect the occurrence of the other, while mutually exclusive events are events that cannot occur at the same time.

How do you calculate the probability of an event?

The probability of an event is calculated using the formula P = n(A) / n(S), where n(A) is the number of favorable outcomes and n(S) is the total number of outcomes in the sample space.

What does it mean when an event is 'impossible'?

An event is considered impossible if the outcome is not part of the sample space. For example, if a bag contains only red, green, and yellow marbles, drawing a blue marble is impossible.

What is meant by 'compound events'?

Compound events refer to events that involve two or more individual events. These can be either independent or dependent, and may include 'or' (union) or 'and' (intersection) conditions.

In the case of throwing two dice, what is the probability of getting a sum of 11?

When two dice are thrown, the probability of getting a sum of 11 is P = n(A) / n(S). There are 2 favorable outcomes (5, 6 and 6, 5) and 36 possible outcomes in total, so the probability is 2/36, or 1/18.

How do you calculate the expected frequency for an event?

The expected frequency is calculated by multiplying the probability of an event by the number of trials. For example, if the probability of an event is 1/8 and the event is repeated 50 times, the expected frequency would be (1/8) * 50 = 6.25.

What is the significance of a Venn diagram in probability?

A Venn diagram is used to visually represent the relationships between different events, such as union, intersection, and complement. It helps in understanding how different events overlap or are mutually exclusive.

How do you define mutually exclusive events in terms of dice rolls?

In the case of dice rolls, mutually exclusive events would be those where one event cannot happen if the other occurs. For example, rolling a 2 and rolling a 5 are mutually exclusive, as you cannot roll both at the same time.