#kongruen Kongruen (1) - Syarat dua bangun kongruen #matematikasmpkelas9
Summary
TLDRIn this educational video, the instructor discusses the concept of congruence in geometry, focusing on triangles and various shapes like parallelograms and kites. Key principles are highlighted, including the need for equal corresponding angles and sides for two shapes to be congruent. Through practical examples and calculations, such as using the Pythagorean theorem, the instructor illustrates how to determine congruence in different geometric figures. The video emphasizes the importance of understanding congruence in geometry and encourages viewers to practice these concepts for better comprehension.
Takeaways
- 😀 Congruence in geometry is explored, specifically focusing on triangles.
- 😀 To determine if two shapes are congruent, corresponding angles and sides must be equal.
- 😀 Visual comparisons of shapes can help identify congruence at a glance.
- 😀 Examples are given using specific geometric shapes like triangles and parallelograms.
- 😀 Angles in parallelograms can be calculated using properties of supplementary angles.
- 😀 When two shapes share equal angles and sides, they are congruent.
- 😀 Congruence can also be demonstrated through practical examples involving familiar objects.
- 😀 The congruence of trapezoids is addressed, along with how to find corresponding side lengths.
- 😀 The Pythagorean theorem is referenced for calculating lengths in right triangles.
- 😀 The importance of understanding geometric properties for further studies in congruence is emphasized.
Q & A
What is the main topic discussed in the video?
-The main topic discussed in the video is the concept of congruence in geometry, particularly focusing on congruent shapes and triangles.
How is congruence defined in the context of geometric shapes?
-Congruence in geometry means that two shapes are identical in size and shape, with corresponding sides and angles that are equal.
What are the criteria for two triangles to be congruent?
-Two triangles are congruent if their corresponding sides and angles are equal, specifically satisfying conditions such as Angle-Side-Angle (ASA) and Side-Side-Side (SSS).
How does the video demonstrate the concept of congruence with physical objects?
-The video uses physical objects, such as a rectangular wafer and an old mobile phone, to visually compare their dimensions and angles to illustrate the concept of congruence.
What are the two primary properties that need to be satisfied for two figures to be considered congruent?
-The two primary properties are that the corresponding angles must be equal, and the lengths of corresponding sides must be the same.
Can two shapes be congruent if their appearances are different?
-Yes, two shapes can be congruent even if they look different, as long as their corresponding sides and angles are equal.
What example is provided in the video to explain congruence using parallelograms?
-The video explains congruence using parallelograms by comparing their angles and sides, showing that if two angles are equal and the lengths of the sides are the same, the parallelograms are congruent.
What is the significance of measuring angles and sides in proving congruence?
-Measuring angles and sides is crucial for proving congruence as it allows us to confirm that the shapes match in size and form, which is essential for geometric comparisons.
How does the video address the relationship between trapezoids and congruence?
-The video mentions a right trapezoid and explains how to determine its congruence by comparing the lengths of its sides and confirming equal angles.
What is the conclusion drawn in the video regarding the study of congruence?
-The video concludes by emphasizing the importance of understanding congruence in geometry, suggesting that viewers will further explore congruence in triangles in future discussions.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Kekongruenan dan Kesebangunan [Part 2] - Kekongruenan Dua Segitiga
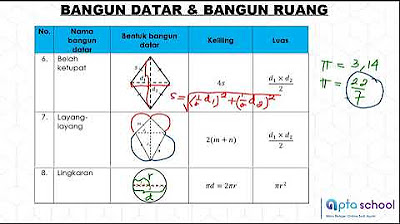
MATERI BANGUN DATAR DAN RUANG

Matematika Kelas 5 SD - Bab 4 Keliling Bangun Datar || Kurikulum Merdeka

MATERI UTBK SNBT PENALARAN MATEMATIKA - BANGUN DATAR
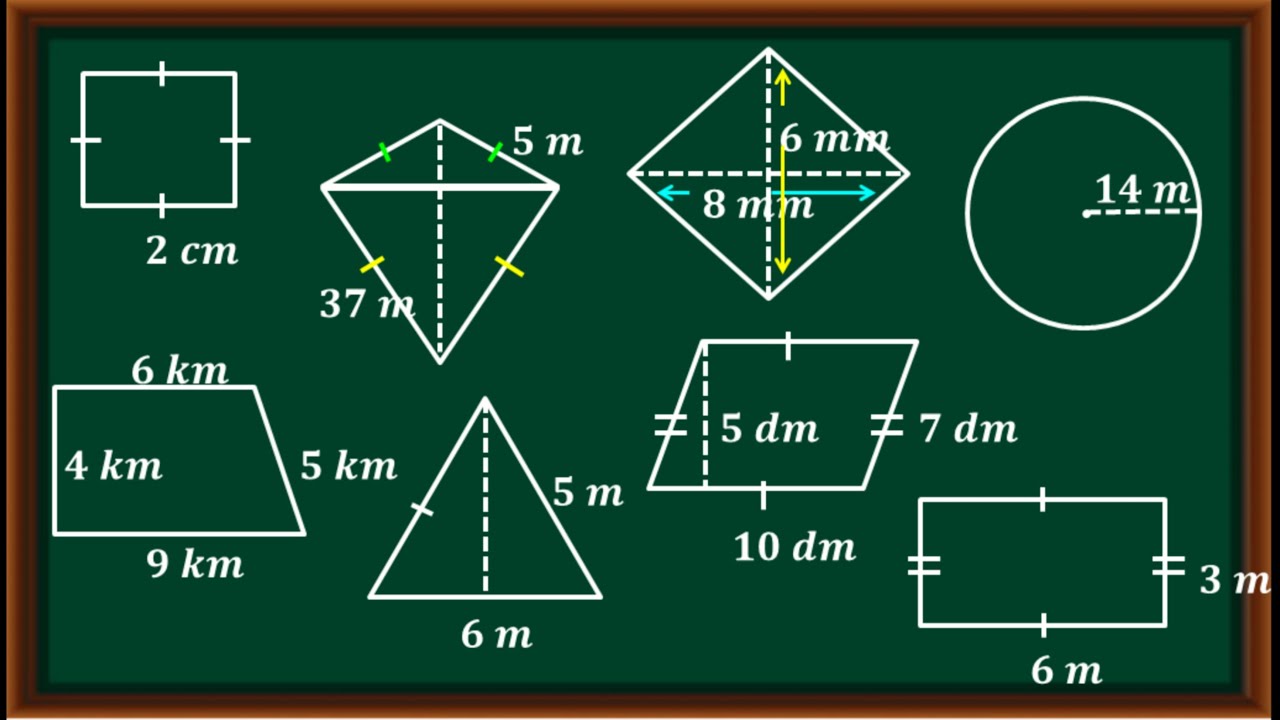
Luas dan keliling bangun datar (Lengkap Semua bangun datar)

Kekongruenan Hal 177-180 Bab 3 TRANSFORMASI Kelas 9 SMP Kurikulum Merdeka
5.0 / 5 (0 votes)