El gradiente de una función - concepto e interpretación
Summary
TLDRThis video provides a detailed explanation of the gradient, focusing on its physical and geometric interpretation. The gradient is introduced as a vector representing the rate of change of a scalar field. The script covers the gradient of functions with two and three independent variables, discussing how to compute and visualize it, both in 2D and 3D. Key properties, such as the gradient's perpendicularity to level curves and surfaces, are explored. The video also includes practical examples, illustrating how the gradient points in the direction of the steepest ascent, making it a fundamental tool in fields like physics and mathematics.
Takeaways
- 😀 The gradient of a scalar function is a vector that represents the rate of change of the function in various directions.
- 😀 A differentiable function is a function that is continuous and can be differentiated, which is a necessary condition for having a gradient.
- 😀 In 2D, the gradient is represented as a vector with components being the partial derivatives of the function with respect to each independent variable.
- 😀 The gradient vector points in the direction of the steepest increase of the function, and its magnitude represents how fast the function increases in that direction.
- 😀 The gradient is normal (perpendicular) to the level curves of the function, which are the curves where the function value remains constant.
- 😀 The gradient helps describe how a scalar field changes as one moves from one point to another, indicating the direction and rate of change.
- 😀 In 3D, the gradient can be extended to three independent variables, and it is normal to the level surface of the function at any given point.
- 😀 The gradient is used in a variety of applications, such as optimization and analyzing physical fields, due to its connection to the directional rate of change.
- 😀 The graphical representation of the gradient in 2D and 3D helps visualize the direction of the steepest increase and the relationship with the function's level curves or surfaces.
- 😀 When the gradient is perpendicular to a curve or surface, it indicates the direction of maximum increase, while directions orthogonal to it correspond to no change in the function.
Please replace the link and try again.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

ADABOOST: GEOMETRIC INTUTION LEC # 425
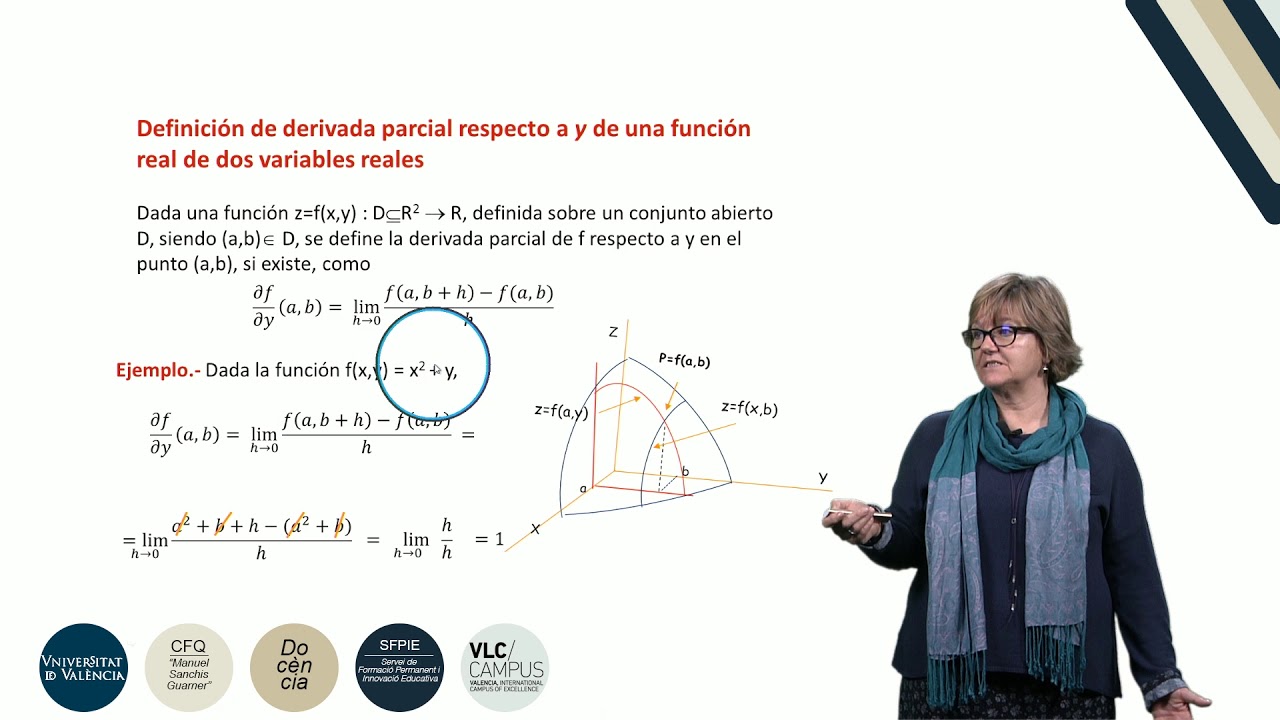
Derivadas parciales. Interpretación geométrica
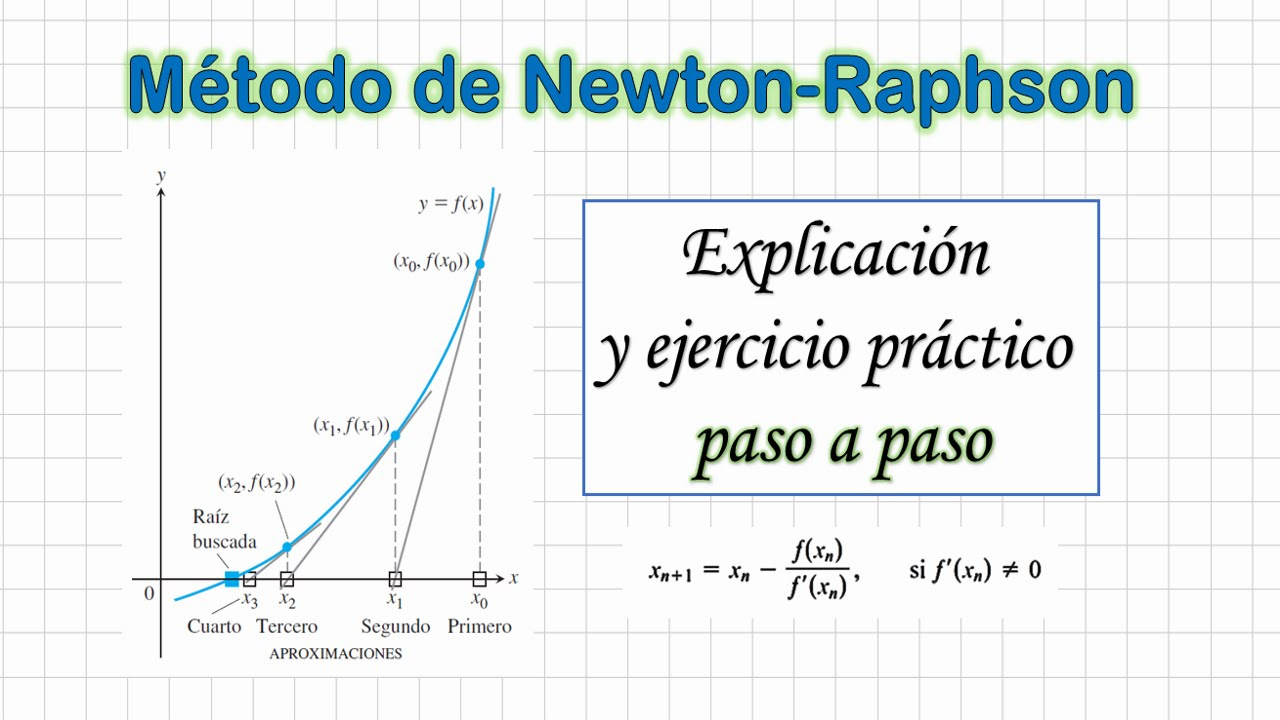
Metodo de Newton-Raphson | Explicación y ejercicio resuelto

Poin Penting Regresi 2 IV (2)

Matematika SMA - Barisan dan Deret (6) - Barisan Geometri, Rumus Un Barisan Geometri (A)

Vektor di Bidang Datar Part 2 (Operasi Pada Vektor) - Matematika Kelas 12
5.0 / 5 (0 votes)