Minimize the given Boolean Function using K-Map then Implement Using Basic Gates | By Mathur Sir
Summary
TLDRThis video tutorial on Microtech channel discusses the minimization of Boolean functions using K-Map (Karnaugh Map). The presenter explains how to minimize a given function, including handling 'don't care' terms. A step-by-step process is provided to create K-Map blocks for four variables, fill the map with values, and group the terms to minimize the function. The explanation includes key concepts like pairing, quads, and rolling maps. Finally, the minimized function is implemented using basic gates (AND, OR, NOT), providing insights into solving K-Map problems efficiently in exams.
Takeaways
- 😀 The video is about K-Map minimization, focusing on reducing a given function using K-maps.
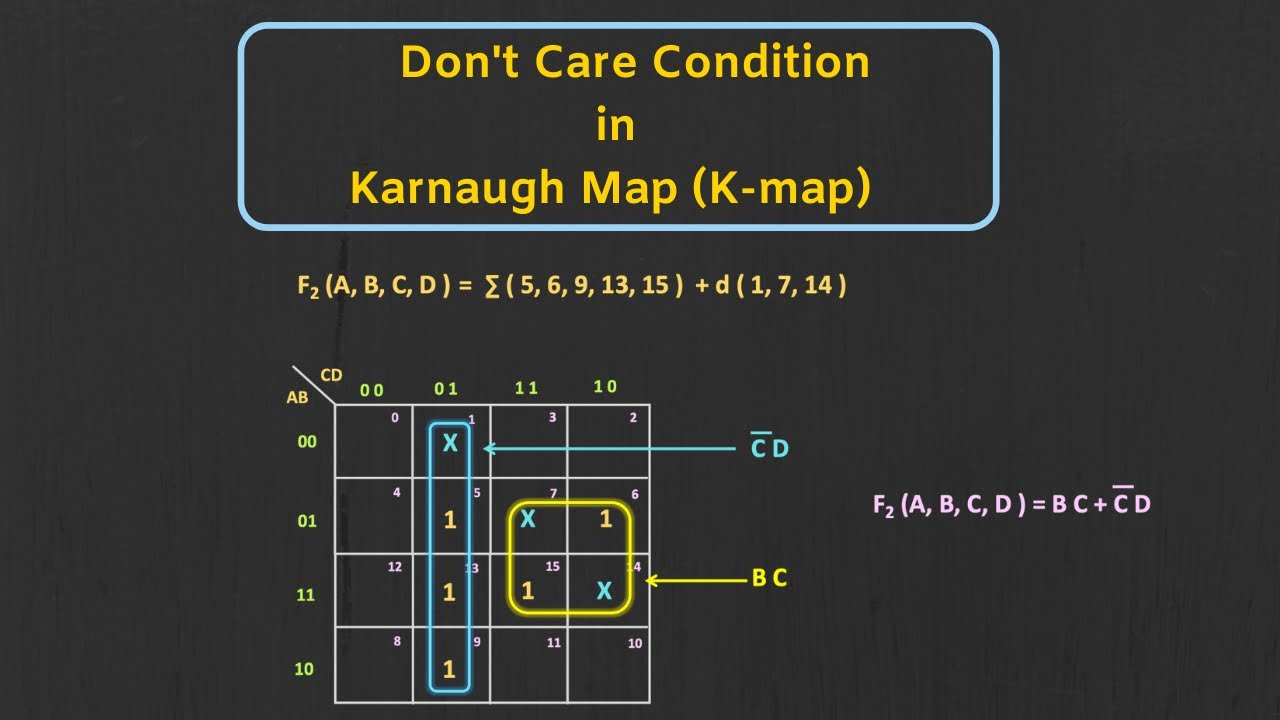
- 😀 A function with 'don't care' terms is provided, indicated by sigma D and sigma small M.
- 😀 For four variables, a K-map will have 16 blocks, determined by 2^4 = 16.
- 😀 The variables A, B, C, and D are labeled on the K-map with their respective complements.
- 😀 The process of assigning '1' values to minterms and 'X' to don't-care terms based on the provided function is explained.
- 😀 Grouping '1's in the K-map is crucial for finding the minimized function; larger groups are preferred.
- 😀 The K-map allows grouping of blocks into pairs, quads, or octets, focusing on minimizing the number of terms.
- 😀 The function is minimized using logical expressions, such as A'B + B'D' + A'BD, based on the grouped K-map results.
- 😀 'Don't care' terms are only used when they help in forming larger groups, otherwise treated as '0'.
- 😀 The minimized function can be implemented using basic gates like AND, OR, and NOT, as demonstrated in the video.
Q & A
What is the main topic of the video?
-The main topic of the video is K-map minimization, which involves minimizing Boolean functions using Karnaugh Maps (K-maps).
How many blocks are created in a K-map with four variables?
-A K-map with four variables will have 2^4 = 16 blocks.
What are 'don't care' conditions in K-maps?
-'Don't care' conditions in K-maps refer to values that can be either 0 or 1, depending on how they affect the grouping. They are used to simplify expressions when they fall into the grouping of 1s.
How are the variables labeled in a 4-variable K-map?
-The variables in a 4-variable K-map are labeled as A, B, C, and D, with their complements (A', B', C', D') assigned to different sections of the map.
What is the significance of numbering the K-map from 0 to 15?
-Numbering the K-map from 0 to 15 corresponds to the binary representation of the minterms. This helps in identifying the locations of 1s, 0s, and 'don't care' values.
How are the minterms and 'don't care' conditions assigned in the K-map?
-Minterms are placed in the cells corresponding to their binary indices, marked with 1. 'Don't care' conditions are represented by crosses and placed in their respective positions based on the given conditions.
What is the goal when grouping in K-map minimization?
-The goal is to create the largest possible groups of 1s and 'don't care' terms to minimize the Boolean function. Groups can be pairs, quads, or octets.
Why is the largest group preferred when minimizing K-maps?
-Larger groups simplify the Boolean expression further by eliminating more variables, leading to a more minimized function.
What is the minimized function obtained from the given K-map example?
-The minimized function obtained from the K-map is F = AB' + B'D' + A'BD.
What basic logic gates are used to implement the minimized function?
-The minimized function can be implemented using basic logic gates such as AND, OR, and NOT gates. Each term of the function represents an AND gate, and the terms are combined using OR gates, with NOT gates used for complemented variables.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

4 Variable K Map | Minimisation of given Function using K Map | By Mathur Sir

Karnaugh Map (K' Map) - Part 1
Don't Care Conditions in Karnaugh Map (with Solved Examples)

3-Variable K-Map | Minimization of 3-Variable POS Function Using K-Map | By Mathur Sir

Quine-McCluskey Minimization Technique (Tabular Method)

101. OCR A Level (H046-H446) SLR15 - 1.4 Karnaugh maps part 4
5.0 / 5 (0 votes)