Divisor de corriente
Summary
TLDREn este video se explica cómo funciona el divisor de corriente, una aplicación de los circuitos en paralelo. Se analizan dos casos principales: cuando se conectan dos resistencias de igual valor y cuando una resistencia es menor que la otra. También se deduce la fórmula del divisor de corriente y se resuelven varios ejemplos prácticos. Además, se muestran diferentes métodos para calcular la corriente en cada resistencia conectada en paralelo, destacando la importancia de la ley de corrientes de Kirchhoff. El video concluye invitando a los espectadores a interactuar y compartir sus opiniones.
Takeaways
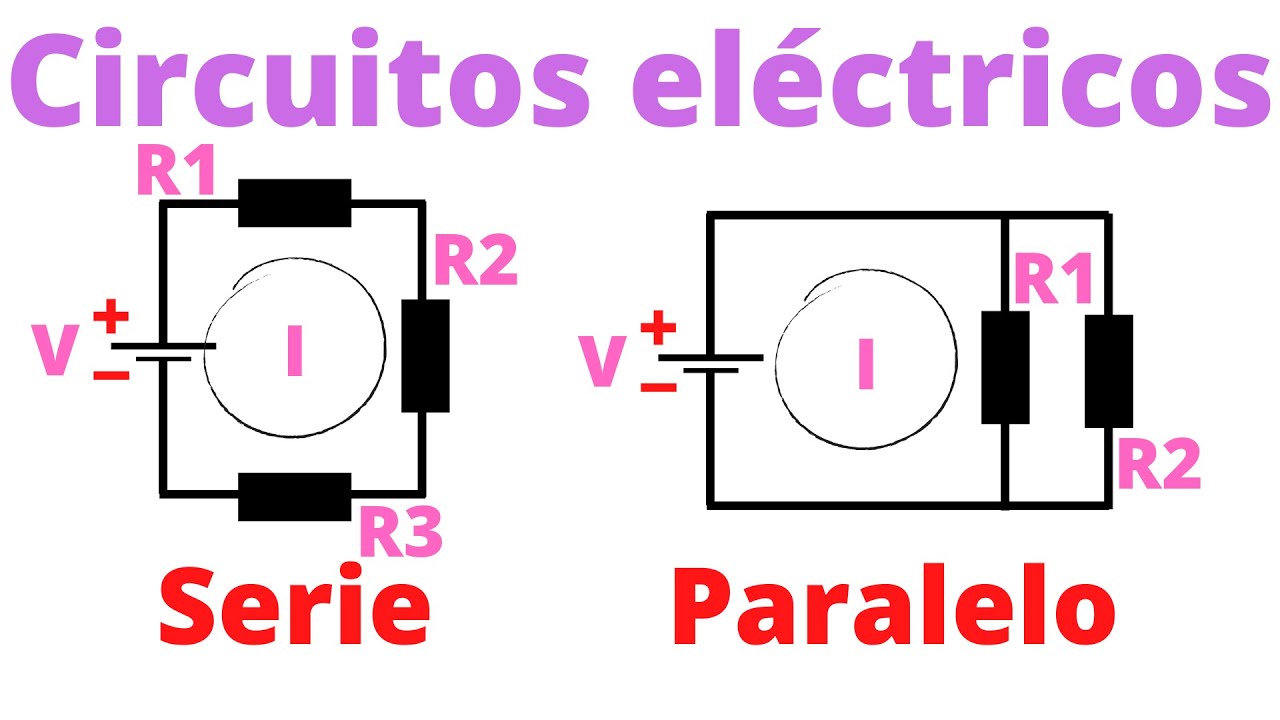
- ⚡ El divisor de corriente es una aplicación de los circuitos en paralelo, donde una corriente se divide en varias ramas con resistencias conectadas en paralelo.
- ➗ Cuando las resistencias son del mismo valor, la corriente se divide en partes iguales entre ellas.
- 🔀 Si una resistencia es menor que otra, la mayor parte de la corriente pasa por la resistencia menor.
- 💡 La fórmula del divisor de corriente permite calcular cuánta corriente pasa por cada resistencia, usando la corriente total y las resistencias individuales.
- 📉 La corriente en una resistencia es igual a la corriente total multiplicada por la resistencia equivalente, dividido entre la resistencia de la rama analizada.
- 📏 En el ejemplo con dos resistencias en paralelo, una corriente de 6 A se divide en 4 A para una resistencia y 2 A para la otra.
- 🔄 La ley de corrientes de Kirchhoff establece que la corriente que entra a un nodo es igual a la suma de las corrientes que salen de ese nodo.
- 🧮 El método de división por relaciones de resistencias facilita calcular cómo se distribuye la corriente cuando varias resistencias están en paralelo.
- 📚 Las fórmulas de divisor de corriente permiten abordar diferentes escenarios, como determinar la corriente en una rama específica o calcular una resistencia desconocida.
- 🔧 Los ejemplos resueltos muestran cómo aplicar las fórmulas del divisor de corriente para analizar circuitos con varias resistencias en paralelo.
Q & A
¿Qué es un divisor de corriente?
-Un divisor de corriente es una aplicación de los circuitos en paralelo que permite distribuir una corriente entre varias resistencias conectadas en paralelo, dependiendo de los valores de estas resistencias.
¿Qué ocurre cuando dos resistencias del mismo valor están conectadas en paralelo?
-Cuando dos resistencias del mismo valor están conectadas en paralelo, la corriente se divide en partes iguales, de modo que cada resistencia recibe la mitad de la corriente total.
¿Cómo se comporta la corriente cuando una resistencia es menor que la otra en un circuito paralelo?
-Cuando una resistencia es menor que la otra en un circuito paralelo, la mayor parte de la corriente pasa por la resistencia menor, ya que ofrece menos oposición al flujo de corriente.
¿Cómo se deduce la fórmula para el divisor de corriente?
-La fórmula del divisor de corriente se deduce utilizando la ley de Ohm y la equivalencia de voltaje en resistencias en paralelo. La corriente que pasa por una resistencia es igual al voltaje de entrada dividido entre el valor de la resistencia, ajustado por la resistencia total del circuito en paralelo.
¿Cómo se calcula la corriente que pasa por una resistencia en un circuito en paralelo?
-Para calcular la corriente que pasa por una resistencia en un circuito en paralelo, se multiplica la corriente total del circuito por la resistencia total del sistema y se divide entre el valor de la resistencia específica.
¿Qué dice la ley de corrientes de Kirchhoff?
-La ley de corrientes de Kirchhoff establece que la suma de las corrientes que entran en un nodo es igual a la suma de las corrientes que salen de él. En el caso de un divisor de corriente, esto significa que la suma de las corrientes parciales en cada rama debe ser igual a la corriente total que entra al nodo.
¿Cómo se calcula la resistencia total de dos resistencias en paralelo?
-La resistencia total de dos resistencias en paralelo se calcula con la fórmula: R_total = (R_1 * R_2) / (R_1 + R_2).
En un ejemplo dado, si hay dos resistencias en paralelo de 4 y 8 ohmios, y una corriente total de 6 amperios, ¿cómo se calcula la corriente que pasa por la resistencia de 8 ohmios?
-Primero se calcula la resistencia total del circuito, que es 8/3 ohmios. Luego, la corriente que pasa por la resistencia de 8 ohmios se calcula multiplicando la corriente total (6 amperios) por la resistencia total (8/3) y dividiendo entre la resistencia específica de 8 ohmios, lo que da una corriente de 2 amperios.
¿Qué sucede si la corriente pasa por tres resistencias en paralelo de 6, 24 y 48 ohmios y la corriente total es de 42 miliamperios?
-Primero se calcula la resistencia total del sistema, que es 48/11 ohmios. Luego, la corriente que pasa por la resistencia de 6 ohmios sería 30.54 miliamperios, calculada multiplicando la corriente total por la resistencia total y dividiéndola por el valor de la resistencia.
¿Cómo se encuentra el valor de una resistencia en un circuito en paralelo si se conoce la corriente que pasa por otra resistencia?
-Para encontrar el valor de una resistencia, se usa la fórmula del divisor de corriente. Se conoce la corriente total, la resistencia de una de las ramas y la corriente que pasa por esa rama. A partir de ahí, se despeja el valor de la resistencia que falta.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
5.0 / 5 (0 votes)